Aufgaben:Exercise 3.4: Optimization of the Cutoff Frequency

• Return to book

Systemgrößen für Binär– und Quaternärsystem sowie für verschiedene Grenzfrequenzen

Wir vergleichen ein redundanzfreies Binärsystem  $(M = 2)$  und ein redundanzfreies Quaternärsystem  $(M = 4)$  hinsichtlich ihrer S/N–Verhältnisse im ungünstigsten Fall:

$$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2} \hspace{0.05cm}.$$

$\ddot{o}(T_{\rm D})$  ist die vertikale Augenöffnung und  $\sigma_d^2$  gibt die Detektionsrauschleistung an. Für beide Systemkonfigurationen gelten die gleichen Randbedingungen (ähnlich wie in  Aufgabe 3.4Z):

• Der rechteckige Sendegrundimpuls  $g_s(t)$  im NRZ–Format hat die Höhe  $s_0 = 1 \, {\rm V}$.
• Die (äquivalente) Bitrate beträgt in beiden Fällen  $R_{\rm B} = 100 \, {\rm Mbit/s}$.
• Der Kanal besteht aus einem Koaxialkabel mit der charakteristischen Kabeldämpfung  $a_* = 80 \, {\rm dB}= 9.2 \, {\rm Np}$.
• Das Empfangsfilter sei ein Gaußtiefpass mit der Grenzfrequenz  $f_{\rm G}$, die zu optimieren ist:

$$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$

• Am Kanalausgang liegt AWGN–Rauschen mit der Rauschleistungsdichte  $N_0$  vor.
• Die Entscheiderschwellen sind optimal gewählt und auch der Detektionszeitpunkt  $T_{\rm D} = 0$  ist bestmöglich.

Im Gegensatz zur  Aufgabe 3.4Z  $($feste Grenzfrequenz  $f_{\rm G} = 30 \, {\rm MHz})$  ist hier die Grenzfrequenz des Tiefpasses variabel. Diese soll so bestimmt werden, dass das ungünstigste S/N–Verhältnis  $\rho_{\rm U}$  maximiert und damit die (ungünstigste) Fehlerwahrscheinlichkeit  $p_{\rm U}$  minimiert wird.

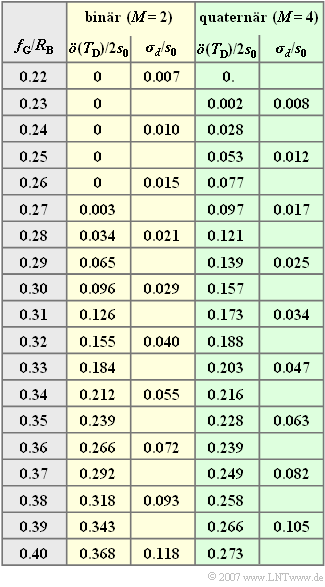
Die Tabelle zeigt

• die (normierte) halbe Augenöffnung und
• den (normierten) Detektionsrauscheffektivwert

für das Binärsystem  $(M = 2)$  und das Quaternärsystem  $(M = 4)$  sowie für verschiedene (normierte) Grenzfrequenzen. Die Normierung basiert dabei auf der Bitrate  $R_{\rm B}$.

Anzumerken ist:

• Die Tabelle gilt für  $E_{\rm B}/N_0 = 5 \cdot 10^8$  und  $a_* = 80 \, {\rm dB}= 9.2 \, {\rm Np}$.
• Die (normierte Rauchleistung ergibt sich unter Berücksichtigung des idealen Kanalentzerrers zu

$$\frac{ \sigma_d^2}{N_{\rm 0} \cdot R_{\rm B}} = \frac{ 1}{R_{\rm B}} \cdot \int_{0}^{\infty}{\rm exp}\left [2 \cdot 9.2 \cdot \sqrt{2 \cdot f/R_{\rm B}} - 2\pi \cdot \frac{(f/R_{\rm B})^2}{(2 f_{\rm G}/R_{\rm B})^2} \right ]{\rm d} \hspace{0.05cm} f \hspace{0.05cm}.$$

• Wie in Aufgabe  Aufgabe 3.4Z  noch hergeleitet wird, gilt für die (normierte) halbe Augenöffnung:

$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( \sqrt{2\pi} \cdot {\rm log_2}\hspace{0.1cm}(M) \cdot {f_{\rm G}}/{R_{\rm B}} \right)\big] \hspace{0.05cm}.$$

• Damit kann für das ungünstigste S/N–Verhältnis geschrieben werden, wobei der letzte Term bei dem hier betrachteten NRZ–Rechteckimpuls als „Energie pro Bit bezogen auf die Rauschleistungsdichte" interpretiert werden kann:

$$\rho_{\rm U} = \left [\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \right ]^2 \cdot \frac{N_{\rm 0} \cdot R_{\rm B}}{ \sigma_d^2} \cdot \frac{ s_0^2}{N_{\rm 0} \cdot R_{\rm B}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Impulsinterferenzen bei mehrstufiger Übertragung.
• In der Tabelle ist  $\sigma_d/s_0$  angegeben, das heißt, dass hier der zweite und der dritte Term obiger Gleichung zusammengefasst sind.
• Durch Division des jeweils ersten Spaltenelements (normierte halbe Augenöffnung) durch das zweite in der Tabelle angegebene Element  $(\sigma_d/s_0)$  und Quadrieren des Quotienten kommt man hier sehr einfach zum Ergebnis  $\rho_{\rm U}$.

Fragebogen

1

Die Tabelle ist bezüglich  $\sigma_d$  nicht vollständig. Ermitteln Sie folgende Werte:

$M = 2, f_{\rm G} = 0.33\text{:}\hspace{0.4cm} \sigma_d/s_0 \ = \ $

$M = 4, f_{\rm G} = 0.28\text{:}\hspace{0.4cm} \sigma_d/s_0 \ = \ $

2

Ermitteln Sie die optimale Grenzfrequenz und den erreichbaren (ungünstigsten) Störabstand für das Binärsystem.

$M = 2\text{:}\hspace{0.9cm} f_{\rm G, \ opt}/R_{\rm B}\ = \ $

$M = 2\text{:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U, \ max}\ = \ $ ${\ \rm dB}$

3

Ermitteln Sie die optimale Grenzfrequenz und den erreichbaren (ungünstigsten) Störabstand für das Quaternärsystem.

$M = 4\text{:}\hspace{0.97cm} f_{\rm G, \ opt}/R_{\rm B}\ = \ $

$M = 4\text{:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U,\ max}\ = \ $ ${\ \rm dB}$

4

Bewerten Sie die Ergebnisse der Teilaufgaben (2) und (3) anhand der folgenden Aussagen. Welche sind zutreffend?

	Ist die normierte Grenzfrequen  $f_{\rm G}/R_{\rm B} ≥ 0.35$, so ist das Binärsystem dem Quaternärsystem überlegen.
	Mit der normierten Grenzfrequenz  $f_{\rm G}/R_{\rm B} = 0.33$  ist das Binärsystem besser als das Quaternärsystem.
	Der Hauptgrund für die Überlegenheit des Quaternärsystems gegenüber dem Binärsystem (jeweils optimiert) ist die niedrigere Symbolrate.
	Aus den vorliegenden Werten kann geschlossen werden, dass das (optimale) Quaternärsystem auch für  $a_* = 100 \, {\rm dB}$  besser ist.
	Aus den vorliegenden Werten kann geschlossen werden, dass das (optimale) Quaternärsystem auch für  $a_* = 40 \, {\rm dB}$  besser ist.

Musterlösung

Solution

(1)  Normiert man die Grenzfrequenz $f_{\rm G}$ auf die Bitrate $R_{\rm B}$ (und nicht auf die Symbolrate $1/T$), so gelten die angegebenen Rauscheffektivwerte unabhängig von der Stufenzahl. Damit erhält man:

$$M = 2, \hspace{0.1cm}f_{\rm G}/R_{\rm B} = 0.33\text{:} \hspace{0.2cm} \sigma_d/s_0 \ \hspace{0.15cm}\underline { = 0.047} \hspace{0.05cm},$$

$$M = 4, \hspace{0.1cm}f_{\rm G}/R_{\rm B} = 0.28\text{:} \hspace{0.2cm} \sigma_d/s_0 \ \hspace{0.15cm}\underline { = 0.021} \hspace{0.05cm}.$$

(2)  Die optimale Grenzfrequenz ist dann gegeben, wenn der Quotient aus (halber) Augenöffnung und Rauscheffektivwert maximal ist.

• Das Optimum ergibt sich beim Binärsystem für $f_{\rm G}/R_{\rm B} \underline {= 0.33}$:

$$\rho_{\rm U,\hspace{0.05cm} max} = \frac{0.184^2}{ 0.047^2} = 15.32 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U,\hspace{0.05cm} max}\hspace{0.15cm}\underline { = 11.85\,{\rm dB}} \hspace{0.05cm}.$$

• Dagegen gilt für die benachbarten Grenzfrequenzwerte:

$$f_{\rm G}/R_{\rm B} = 0.32\text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.155^2}{ 0.040^2} = 15.02 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 11.76\,{\rm dB} \hspace{0.05cm},$$

$$f_{\rm G}/R_{\rm B} = 0.34 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.212^2}{ 0.055^2} = 14.86 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 11.72\,{\rm dB} \hspace{0.05cm}.$$

• Hieraus erkennt man das – wenn auch flache – Optimum.

(3)  Für $M = 4$ erhält man folgende Ergebnisse:

$$f_{\rm G}/R_{\rm B} = 0.27 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.097^2}{ 0.017^2} = 32.56 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 15.13\,{\rm dB} \hspace{0.05cm},$$

$$f_{\rm G}/R_{\rm B} = 0.28 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.121^2}{ 0.021^2} = 33.20 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {= 15.21\,{\rm dB}} \hspace{0.05cm},$$

$$f_{\rm G}/R_{\rm B} = 0.29 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.139^2}{ 0.025^2} = 30.91 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 14.90\,{\rm dB} \hspace{0.05cm}.$$

• Die optimale Grenzfrequenz liegt demnach beim Quaternärsystem bei $f_{\rm G}/R_{\rm B} \underline {= 0.28}$.
• Der Störabstand ist dann um mehr als $3 \, {\rm dB}$ größer als beim Binärsystem mit optimierter Grenzfrequenz.

(4)  Zutreffend sind die Aussagen 1, 3 und 4:

• Die Richtigkeit der ersten Aussage wird durch die Tabelle bestätigt. Für $f_{\rm G}/R_{\rm B} ≥ 0.35$ weist das Binärsystem eine größere Augenöffnung als das Quaternärsystem auf. Durch die Normierung aller Frequenzen auf die Bitrate ist zudem der Rauscheffektivwert unabhängig von der Stufenzahl $M$, so dass die Optimierung auf die Augenöffnung beschränkt werden kann.

• Für $f_{\rm G}/R_{\rm B} < 0.35$ ist dagegen das Quaternärsystem besser, also auch für $f_{\rm G}/R_{\rm B} = 0.33$. Obwohl diese Grenzfrequenz für $M = 2$ optimal ist und für $M = 4$ nicht, ist mit $f_{\rm G}/R_{\rm B} = 0.33$ das Quaternärsystem um etwa $0.85 \, {\rm dB}$ besser als das Binärsystem.

• Die dritte Aussage trifft zu. Durch die niedrigere (genauer gesagt: halbe) Symbolrate ist für $M = 4$ das Auge auch mit $f_{\rm G}/R_{\rm B} = 0.23$ noch geöffnet, während bei einem Binärsystem bereits für $f_{\rm G}/R_{\rm B} = 0.27$ ein (fast) geschlossenes Auge vorliegt.

• Mit größerer charakteristischer Kabeldämpfung geht die Tendenz zu immer kleinerer Grenzfrequenz, um die Anhebung des Rauschens möglichst gering zu halten. Wenn aber bereits bei $a_* = 80 \, {\rm dB}$ das (bezüglich der Grenzfrequenz optimierte) Quaternärsystem besser ist, so gilt das auch für $100 \, {\rm dB}$. Der Gewinn ist größer als $15.21 \, – \, 11.85 \approx 3.4 \, {\rm dB}$. Diese Werte wurden in den Aufgaben (2) und (3) ermittelt.

• Dagegen ist für die charakteristische Kabeldämpfung $a_* = 40 \, {\rm dB}$ anhand des vorliegenden Zahlenmaterials keine Aussage möglich. Eine Systemsimulation lieferte hierfür folgende Ergebnisse $($für $E_{\rm B}/N_0 = 50 \, {\rm dB})$:

$$M =2\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 15.43\,{\rm dB} \hspace{0.2cm}{\rm mit}\hspace{0.2cm} f_{\rm G}/R_{\rm B} \approx 0.4 \hspace{0.05cm},$$

$$M =4\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 14.65\,{\rm dB} \hspace{0.2cm}{\rm mit}\hspace{0.2cm} f_{\rm G}/R_{\rm B} \approx 0.32 \hspace{0.05cm}.$$