Difference between revisions of "Aufgaben:Exercise 1.7: Entropy of Natural Texts"
| (32 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Natural_Discrete_Sources |
}} | }} | ||
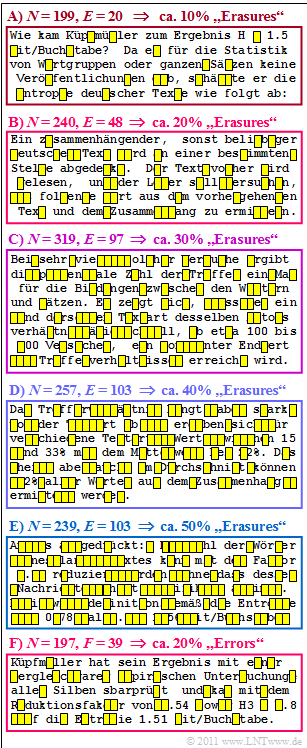
| − | [[File: | + | [[File:Inf_A_1_7_v2.png|right|frame|Text with erasures or errors]] |
| − | : | + | In the early 1950s, [https://en.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] estimated the entropy $H$ of the English language at one bit per character. A short time later, [https://en.wikipedia.org/wiki/Karl_K%C3%BCpfm%C3%BCller Karl Küpfmüller] arrived at an entropy value of $H =1.3\ \rm bit/character$, i.e. a somewhat larger value, in an empirical study of the German language. Interestingly, the results of Shannon and Küpfmüller are based on two completely different methods. |
| − | + | The differing results cannot be explained by the small differences in the range of symbols $M$ : | |
| − | + | * Shannon assumed $26$ letters and the space ⇒ $M = 27$. | |
| + | * Küpfmüller assumed only $M = 26$ letters (i.e. without the "Blank Space"). | ||
| − | |||
| − | + | Both made no distinction between upper and lower case. | |
| − | + | This task is intended to show how | |
| + | * "Erasures" ⇒ one knows the location of an error, resp. | ||
| + | * "Errors" ⇒ it is not clear to the reader what is wrong and what is right, | ||
| − | |||
| − | + | have an effect on the comprehensibility of a text. Our text also contains the typical German letters "ä", "ö", "ü" and "ß" as well as numbers and punctuation. In addition, a distinction is made between upper and lower case. | |
| − | |||
| − | |||
| − | + | In the figure, a text dealing with Küpfmüller's approach is divided into six blocks of length between $N = 197$ and $N = 319$. Described is the check of his [[Information_Theory/Natürliche_wertdiskrete_Nachrichtenquellen#A_further_entropy_estimation_by_K.C3.BCpfm.C3.BCller|first analysis]] in a completely different way, which led to the result $H =1.51\ \rm bit/character$. | |
| − | + | * In the upper five blocks one recognises "Erasures" with different erasure probabilities between $10\%$ and $50\%$. | |
| + | * In the last block, "character errors" with $20$–error probability are inserted. | ||
| − | |||
| − | : | + | The influence of such character errors on the readability of a text is to be compared in subtask '''(4)''' with the second block (outlined in red), for which the probability of an erasure is also $20\%$. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Natürliche_wertdiskrete_Nachrichtenquellen|Natural Discrete Sources]]. | ||
| + | *Bezug genommen wird insbesondere auf die beiden Seiten | ||
| + | ::[[Information_Theory/Natürliche_wertdiskrete_Nachrichtenquellen#Entropy_estimation_according_to_K.C3.BCpfm.C3.BCller|Entropy estimation according to Küpfmüller]], sowie | ||
| + | ::[[Information_Theory/Natural_Discrete_Sources#A_further_entropy_estimation_by_K.C3.BCpfm.C3.BCller|A further entropy estimation by Küpfmüller]]. | ||
| + | |||
| + | *For the '''relative redundancy''' of a sequence with the decision content $H_0$ and the entropy $H$ applies | ||
:$$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$ | :$$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$ | ||
| + | *To solve the subtask '''(4)''' you need a good knowledge of the German language. | ||
| − | === | + | |
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Here is the English translation of the six description blocks:}$ | ||
| + | |||
| + | $\rm (A)$ How did Küpfmüller arrive at the result H = 1.51 bit/character? Since there were no publications for the statistics of word groups or whole sentences, he estimated the entropy of the German language as follows: | ||
| + | |||
| + | $\rm (B)$ A coherent, otherwise arbitrary German text is covered at a certain point. The text before is read and the reader is asked to try to determine the following word from the previous text and the context. | ||
| + | |||
| + | $\rm (C)$ With a very large number of such attempts, the percentage of hits gives a measure of the bonds between the words and sentences. It turns out that for one and the same type of text by the same author, a constant final value of the hit ratio is reached relatively quickly, from about 100 to 200 attempts. | ||
| + | |||
| + | $\rm (D)$ The hit ratio depends strongly on the type of text. Values between 15% and 33% are obtained for different types of text, with an average value of 22%. However, this also means that on average 22% of all words can be determined from the context. | ||
| + | |||
| + | $\rm (E)$ In other words, the number of words in a long text can be reduced by a factor of 0.78 without significantly reducing its message content. By definition, the entropy H = 0.78 times 2.0 = 1.56 bit/character. | ||
| + | |||
| + | $\rm (F)$ Küpfmüller checked his result with a comparable empirical investigation of all syllables and came up with the reduction factor 0.54 and H3= 2.8 to the entropy H = 1.51 bit/character.}} | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What symbol set size $M$ did Küpfmüller assume? |
|type="{}"} | |type="{}"} | ||
| − | $M$ | + | $M \ = \ $ { 26 } |
| − | { | + | {What relative redundancy $r$ results from Küpfmüller's entropy value? |
|type="{}"} | |type="{}"} | ||
| − | $r$ | + | $r \ = \ $ { 72.3 3% } $\ \%$ |
| − | { | + | {How can the result of subtask '''(2)''' be interpreted? Assume a text file with $M = 26$ different characters. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Such a text file of sufficient length $(N \to \infty)$ could be represented with $1.3 \cdot N$ binary symbols. |
| − | - | + | - Such a text file with $N= 100\hspace{0.05cm}000$ characters could be represented with $130\hspace{0.1cm}000$ binary symbols. |
| − | - | + | - A reader can still understand (or at least guess) the text even if $70\%$ of the characters are erased. |
| − | { | + | {What makes a text more difficult to understand? |
| − | |type=" | + | |type="()"} |
| − | - 20% | + | - $20\%$ erasures, |
| − | + | + | + $20\%$ errors. |
| Line 61: | Line 93: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The symbol set size in Küpfmüller's investigations was $\underline{M = 26}$, because, in contrast to Shannon, he did not initially take the space into account. | |
| − | + | In the given German text of this task, the symbol set size is significantly larger, | |
| + | * since the typical German characters "ä", "ö", "ü" and "ß" also occur, | ||
| + | * there is a distinction between upper and lower case, | ||
| + | * and there are also numbers and punctuation marks. | ||
| − | |||
| − | : | + | '''(2)''' With the decision content $H_0 = \log_2 \ (31) \approx 4.7 \ \rm bit/character$ and the entropy $H = 1.3\ \rm bit/character $ , one obtains for the relative redundancy: |
| + | :$$r = \frac{H_0 - H}{H_0}= \frac{4.7 - 1.3}{4.7}\underline {\hspace{0.1cm}\approx 72.3\,\%}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | + | '''(3)''' Only the <u>first suggested solution</u> is correct: | |
| + | *According to Küpfmüller, one only needs $1.3$ binary characters per source character. | ||
| + | *With a file of length $N$ , $1.3 \cdot N$ binary symbols would therefore be sufficient, but only if the source symbol sequence is infinitely long $(N \to \infty)$ and this was encoded in the best possible way. | ||
| + | *In contrast, Küpfmüller's result and the relative redundancy of more than $70\%$ calculated in subtask '''(2)''' do not mean that a reader can still understand the text if $70\%$ of the characters have been erased. | ||
| + | *Such a text is neither infinitely long nor has it been optimally encoded beforehand. | ||
| + | |||
| − | |||
| − | :* | + | '''(4)''' Correct is <u>statement 2</u>: |
| + | *Test it yourself: The second block of the graphic on the information page is easier to decode than the last block, because you know where there are errors. | ||
| + | *If you want to keep trying: The exact same sequence of character errors was used for the bottom block '''(F)''' as for block '''(B)''' , that is, there are errors at characters $6$, $35$, $37$, and so on. | ||
| − | |||
| − | : | + | [[File:Inf_A_1_7d_v2.png|right|frame|Original texts]] |
| + | Finally, the original text is given, which is only reproduced on the information page distorted by erasures or real character errors. | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.3 Natural Discrete Sources^]] |
Latest revision as of 13:06, 10 August 2021
In the early 1950s, Claude E. Shannon estimated the entropy $H$ of the English language at one bit per character. A short time later, Karl Küpfmüller arrived at an entropy value of $H =1.3\ \rm bit/character$, i.e. a somewhat larger value, in an empirical study of the German language. Interestingly, the results of Shannon and Küpfmüller are based on two completely different methods.
The differing results cannot be explained by the small differences in the range of symbols $M$ :
- Shannon assumed $26$ letters and the space ⇒ $M = 27$.
- Küpfmüller assumed only $M = 26$ letters (i.e. without the "Blank Space").
Both made no distinction between upper and lower case.
This task is intended to show how
- "Erasures" ⇒ one knows the location of an error, resp.
- "Errors" ⇒ it is not clear to the reader what is wrong and what is right,
have an effect on the comprehensibility of a text. Our text also contains the typical German letters "ä", "ö", "ü" and "ß" as well as numbers and punctuation. In addition, a distinction is made between upper and lower case.
In the figure, a text dealing with Küpfmüller's approach is divided into six blocks of length between $N = 197$ and $N = 319$. Described is the check of his first analysis in a completely different way, which led to the result $H =1.51\ \rm bit/character$.
- In the upper five blocks one recognises "Erasures" with different erasure probabilities between $10\%$ and $50\%$.
- In the last block, "character errors" with $20$–error probability are inserted.
The influence of such character errors on the readability of a text is to be compared in subtask (4) with the second block (outlined in red), for which the probability of an erasure is also $20\%$.
Hints:
- The exercise belongs to the chapter Natural Discrete Sources.
- Bezug genommen wird insbesondere auf die beiden Seiten
- For the relative redundancy of a sequence with the decision content $H_0$ and the entropy $H$ applies
- $$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$
- To solve the subtask (4) you need a good knowledge of the German language.
$\text{Here is the English translation of the six description blocks:}$
$\rm (A)$ How did Küpfmüller arrive at the result H = 1.51 bit/character? Since there were no publications for the statistics of word groups or whole sentences, he estimated the entropy of the German language as follows:
$\rm (B)$ A coherent, otherwise arbitrary German text is covered at a certain point. The text before is read and the reader is asked to try to determine the following word from the previous text and the context.
$\rm (C)$ With a very large number of such attempts, the percentage of hits gives a measure of the bonds between the words and sentences. It turns out that for one and the same type of text by the same author, a constant final value of the hit ratio is reached relatively quickly, from about 100 to 200 attempts.
$\rm (D)$ The hit ratio depends strongly on the type of text. Values between 15% and 33% are obtained for different types of text, with an average value of 22%. However, this also means that on average 22% of all words can be determined from the context.
$\rm (E)$ In other words, the number of words in a long text can be reduced by a factor of 0.78 without significantly reducing its message content. By definition, the entropy H = 0.78 times 2.0 = 1.56 bit/character.
$\rm (F)$ Küpfmüller checked his result with a comparable empirical investigation of all syllables and came up with the reduction factor 0.54 and H3= 2.8 to the entropy H = 1.51 bit/character.
Questions
Solution
In the given German text of this task, the symbol set size is significantly larger,
- since the typical German characters "ä", "ö", "ü" and "ß" also occur,
- there is a distinction between upper and lower case,
- and there are also numbers and punctuation marks.
(2) With the decision content $H_0 = \log_2 \ (31) \approx 4.7 \ \rm bit/character$ and the entropy $H = 1.3\ \rm bit/character $ , one obtains for the relative redundancy:
- $$r = \frac{H_0 - H}{H_0}= \frac{4.7 - 1.3}{4.7}\underline {\hspace{0.1cm}\approx 72.3\,\%}\hspace{0.05cm}.$$
(3) Only the first suggested solution is correct:
- According to Küpfmüller, one only needs $1.3$ binary characters per source character.
- With a file of length $N$ , $1.3 \cdot N$ binary symbols would therefore be sufficient, but only if the source symbol sequence is infinitely long $(N \to \infty)$ and this was encoded in the best possible way.
- In contrast, Küpfmüller's result and the relative redundancy of more than $70\%$ calculated in subtask (2) do not mean that a reader can still understand the text if $70\%$ of the characters have been erased.
- Such a text is neither infinitely long nor has it been optimally encoded beforehand.
(4) Correct is statement 2:
- Test it yourself: The second block of the graphic on the information page is easier to decode than the last block, because you know where there are errors.
- If you want to keep trying: The exact same sequence of character errors was used for the bottom block (F) as for block (B) , that is, there are errors at characters $6$, $35$, $37$, and so on.
Finally, the original text is given, which is only reproduced on the information page distorted by erasures or real character errors.