Difference between revisions of "Aufgaben:Exercise 3.6: Partitioning Inequality"
| Line 3: | Line 3: | ||
}} | }} | ||
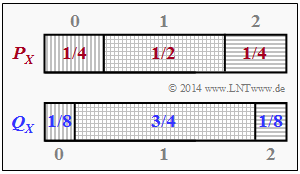
| − | [[File:P_ID2812__Inf_A_3_5.png|right|frame| | + | [[File:P_ID2812__Inf_A_3_5.png|right|frame|Probability functions $P_X$, $Q_X$]] |
| − | + | The ''Kullback–Leibler distance'' (KLD for short) is also used in the ''Partition Unequality'': | |
| − | * | + | * We assume the set $X = \{ x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M \}$ and the probability functions |
:$$P_X(X) = P_X ( x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M )\hspace{0.05cm},$$ | :$$P_X(X) = P_X ( x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M )\hspace{0.05cm},$$ | ||
:$$Q_X(X) =Q_X ( x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M ), $$ | :$$Q_X(X) =Q_X ( x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M ), $$ | ||
| − | : | + | :which are said to be "similar in some way". |
| − | * | + | * We divide the set $X$ into partitions $A_1, \text{...} , A_K$, which are [[Theory_of_Stochastic_Signals/Mengentheoretische_Grundlagen#Disjunkte_Mengen|disjoint]] to each other and result in a [[Theory_of_Stochastic_Signals/Mengentheoretische_Grundlagen#Vollst.C3.A4ndiges_System|complete system]] : |
:$$\bigcup_{i=1}^{K} = X, \hspace{0.5cm} A_i \cap A_j = {\it \phi} \hspace{0.25cm}\text{für}\hspace{0.25cm} 1 \le i \ne j \le K .$$ | :$$\bigcup_{i=1}^{K} = X, \hspace{0.5cm} A_i \cap A_j = {\it \phi} \hspace{0.25cm}\text{für}\hspace{0.25cm} 1 \le i \ne j \le K .$$ | ||
| − | * | + | * In the following, we denote the probability functions with respect to the partitionings $A_1,\ A_2, \text{...} ,\ A_K$ by |
:$$P_X^{\hspace{0.15cm}(A)} = \big [ P_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm},P_X ( A_K ) \big ],\hspace{0.05cm}\hspace{0.5cm}{\rm wobei}\hspace{0.15cm} P_X ( A_i ) = \sum_{ x \in A_i} P_X ( x )\hspace{0.05cm},$$ | :$$P_X^{\hspace{0.15cm}(A)} = \big [ P_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm},P_X ( A_K ) \big ],\hspace{0.05cm}\hspace{0.5cm}{\rm wobei}\hspace{0.15cm} P_X ( A_i ) = \sum_{ x \in A_i} P_X ( x )\hspace{0.05cm},$$ | ||
:$$Q_X^{\hspace{0.15cm}(A)}= \big [ Q_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm},Q_X ( A_K ) \big ],\hspace{0.05cm}\hspace{0.40cm}{\rm wobei}\hspace{0.15cm} Q_X ( A_i ) = \sum_{ x \in A_i} Q_X ( x )\hspace{0.05cm}. $$ | :$$Q_X^{\hspace{0.15cm}(A)}= \big [ Q_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm},Q_X ( A_K ) \big ],\hspace{0.05cm}\hspace{0.40cm}{\rm wobei}\hspace{0.15cm} Q_X ( A_i ) = \sum_{ x \in A_i} Q_X ( x )\hspace{0.05cm}. $$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Please note:}$ The '''partitioning inequality''' yields the following size relation with respect to the Kullback-Leibler distances: |
:$$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) | :$$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) | ||
\hspace{0.25cm}\le \hspace{0.25cm}D(P_X \hspace{0.05cm}\vert \vert \hspace{0.05cm} Q_X) \hspace{0.05cm}.$$}} | \hspace{0.25cm}\le \hspace{0.25cm}D(P_X \hspace{0.05cm}\vert \vert \hspace{0.05cm} Q_X) \hspace{0.05cm}.$$}} | ||
| − | In | + | In subtask '''(1)''' the Kullback-Leibler distance of the two probability functions $P_X(X)$ and $Q_X(X)$ for $X = \{0,\ 1,\ 2\}$ ⇒ $|X| = 3$ is to be determined. |
| − | * | + | *Then the setnbsp; $X$ is to be partitioned with $K = 2$ according to |
| − | :* $A = \{A_1 ,\ A_2\}$ | + | :* $A = \{A_1 ,\ A_2\}$ with $A_1 =\{0\}$ and $A_2 = \{ 1,\ 2 \}$ , |
| − | :* $B = \{B_1 ,\ B_2\}$ | + | :* $B = \{B_1 ,\ B_2\}$ with $B_1 =\{1\}$ and $B_2 = \{ 0,\ 2 \}$, |
| − | :* $C = \{C_1 ,\ C_2\}$ | + | :* $C = \{C_1 ,\ C_2\}$ with $C_1 =\{2\}$ and $C_2 = \{ 0,\ 1\}$, |
| − | * | + | *Then the respective Kullback-Leibler distances are to be given: |
:* $D(P_X^{ (A) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (A) } )$, | :* $D(P_X^{ (A) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (A) } )$, | ||
:* $D(P_X^{ (B) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (B) } )$, | :* $D(P_X^{ (B) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (B) } )$, | ||
:* $D(P_X^{ (C) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (C) } )$. | :* $D(P_X^{ (C) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (C) } )$. | ||
| − | * | + | *Finally, subtask '''(5)''' asks for the conditions that must be satisfied for the equal sign to be true in the above inequality. |
| Line 45: | Line 45: | ||
| − | + | Hints: | |
| − | * | + | *The task belongs to the chapter [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Some preliminary remarks on 2D random variables]]. |
| − | * | + | *In particular, reference is made to the page [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Informational_divergence_-_Kullback-Leibler_distance|Informational Divergence – Kullback-Leibler distance]]. |
| − | * | + | *The two probability functions can be read from the above graph as follows: |
:$$P_X(X) = \big [1/4 , \ 1/2 , \ 1/4 \big ],\hspace{0.5cm} Q_X(X) = \big [1/8, \ 3/4, \ 1/8 \big].$$ | :$$P_X(X) = \big [1/4 , \ 1/2 , \ 1/4 \big ],\hspace{0.5cm} Q_X(X) = \big [1/8, \ 3/4, \ 1/8 \big].$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the Kullback-Leibler distance (KLD) in general. |
|type="{}"} | |type="{}"} | ||
$ D(P_X \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X) \ = \ $ { 0.2075 3% } $\ \rm bit$ | $ D(P_X \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X) \ = \ $ { 0.2075 3% } $\ \rm bit$ | ||
| − | { | + | {WWhat is the Kullback-Leibler distance for the partition $ A_1 = \{0\},\ A_2 = \{1, 2\}$? |
|type="{}"} | |type="{}"} | ||
$D(P_X^{ (A) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (A) } ) \ = \ $ { 0.0832 3% } $\ \rm bit$ | $D(P_X^{ (A) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (A) } ) \ = \ $ { 0.0832 3% } $\ \rm bit$ | ||
| − | { | + | {What is the Kullback-Leibler distance for the partition $ B_1 = \{1\}, \ B_2 = \{0, 2\}$? |
|type="{}"} | |type="{}"} | ||
$D(P_X^{ (B) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (B) } ) \ = \ $ { 0.2075 3% } $\ \rm bit$ | $D(P_X^{ (B) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (B) } ) \ = \ $ { 0.2075 3% } $\ \rm bit$ | ||
| − | { | + | {What is the Kullback-Leibler distance for the partition $ C_1 = \{2\},\ C_2 = \{0, 1\}$? |
|type="()"} | |type="()"} | ||
| − | + | + | + The same result as for partition $A$. |
| − | - | + | - The same result as for partition $B$. |
| − | - | + | - A completely different result. |
| − | { | + | {Under which conditions does equality result for genera $K$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $|X|$ equations must be fulfilled. |
| − | + | + | + For $x \in A_i$ must hold: $P_X(x)/Q_X(x) = P_X(A_i)/ Q_X(A_i)$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the Kullback-Leibler distance holds: |
:$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm}X} | :$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm}X} | ||
| Line 98: | Line 98: | ||
| − | '''(2)''' | + | '''(2)''' With $\text{partition A}$ ⇒ $A_1 = \{0\}$ , $A_2 = \{ 1 , 2 \}$ we get $P_X^{ (A) } (X) = \{1/4 , \ 3/4\}$ and $Q_X^{ (A) } (X) = \{1/8 , \ 7/8\}$. From this follows: |
:$$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm}|| \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) = \frac{1}{4}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/4}{1/8} + | :$$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm}|| \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) = \frac{1}{4}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/4}{1/8} + | ||
| Line 106: | Line 106: | ||
| − | '''(3)''' | + | '''(3)''' With $\text{partition B}$ ⇒ $B_1 = \{1\}$ , $B_2 = \{ 0 ,\ 2 \}$ the probability functions are $P_X^{ (B) } (X) = \{1/2 , \ 1/2\}$ und $Q_X^{ (B) } (X) = \{3/4 , \ 1/4\}$. |
| − | * | + | *Analogous to subtask '''(2)''' one thus obtains: |
:$$D(P_X^{\hspace{0.15cm}(B)} \hspace{0.05cm}|| \hspace{0.05cm} Q_X^{\hspace{0.15cm}(B)}) = \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{3/4} + | :$$D(P_X^{\hspace{0.15cm}(B)} \hspace{0.05cm}|| \hspace{0.05cm} Q_X^{\hspace{0.15cm}(B)}) = \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{3/4} + | ||
\frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{1/4} \hspace{0.15cm} \underline {=0.2075\,{\rm (bit)}} | \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{1/4} \hspace{0.15cm} \underline {=0.2075\,{\rm (bit)}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The result agrees with that of subtask '''(1)''' ⇒ With $\text{partition B}$ the equal sign applies. |
| − | '''(4)''' | + | '''(4)''' With $\text{partition C}$ ⇒ $C_1 = \{2\}$ , $C_2 = \{ 0 , \ 1\}$ one obtains $P_X^{ (C) } (X) = \{1/4, \ 3/4\}$ , $Q_X^{ (C) } (X) = \{1/8, \ 7/8\}$, <br>i.e. the same functions as for the $\text{partition A}$ ⇒ <u>solution proposal 1</u>. |
| − | '''(5)''' | + | '''(5)''' The $\text{partition C}$ has led to the result $D(P_X^{ (B) } \hspace{0.05cm} || \hspace{0.05cm}Q_X^{ (B) } ) = D(P_X \hspace{0.05cm} || \hspace{0.05cm}Q_X)$ geführt. |
| − | * | + | *So for this case |
:$$\frac{P_X(1)}{Q_X(1)} = \frac{1/2}{3/4} = \frac{2}{3}, \ \frac{P_X(B_1)}{Q_X(B_1)} = \frac{1/2}{3/4} = {2}/{3},$$ | :$$\frac{P_X(1)}{Q_X(1)} = \frac{1/2}{3/4} = \frac{2}{3}, \ \frac{P_X(B_1)}{Q_X(B_1)} = \frac{1/2}{3/4} = {2}/{3},$$ | ||
:$$\frac{P_X(0)}{Q_X(0)} = \frac{1/4}{1/8} = 2, \ \frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2,$$ | :$$\frac{P_X(0)}{Q_X(0)} = \frac{1/4}{1/8} = 2, \ \frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2,$$ | ||
:$$\frac{P_X(2)}{Q_X(2)} = \frac{1/4}{1/8} = 2, \ \frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2.$$ | :$$\frac{P_X(2)}{Q_X(2)} = \frac{1/4}{1/8} = 2, \ \frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2.$$ | ||
| − | * | + | *It must therefore hold for all $x \in X$ : |
:$$\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_1)}{Q_X(B_1)}, \text{falls } x \in B_1, \hspace{0.5cm}\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_2)}{Q_X(B_2)}, \text{falls } x \in B_2.$$ | :$$\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_1)}{Q_X(B_1)}, \text{falls } x \in B_1, \hspace{0.5cm}\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_2)}{Q_X(B_2)}, \text{falls } x \in B_2.$$ | ||
| − | * | + | *By generalisation, one can see that <u>both proposed solutions</u> are correct. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 20:14, 26 August 2021
The Kullback–Leibler distance (KLD for short) is also used in the Partition Unequality:
- We assume the set $X = \{ x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M \}$ and the probability functions
- $$P_X(X) = P_X ( x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M )\hspace{0.05cm},$$
- $$Q_X(X) =Q_X ( x_1, \hspace{0.15cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.15cm} x_M ), $$
- which are said to be "similar in some way".
- We divide the set $X$ into partitions $A_1, \text{...} , A_K$, which are disjoint to each other and result in a complete system :
- $$\bigcup_{i=1}^{K} = X, \hspace{0.5cm} A_i \cap A_j = {\it \phi} \hspace{0.25cm}\text{für}\hspace{0.25cm} 1 \le i \ne j \le K .$$
- In the following, we denote the probability functions with respect to the partitionings $A_1,\ A_2, \text{...} ,\ A_K$ by
- $$P_X^{\hspace{0.15cm}(A)} = \big [ P_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm},P_X ( A_K ) \big ],\hspace{0.05cm}\hspace{0.5cm}{\rm wobei}\hspace{0.15cm} P_X ( A_i ) = \sum_{ x \in A_i} P_X ( x )\hspace{0.05cm},$$
- $$Q_X^{\hspace{0.15cm}(A)}= \big [ Q_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm},Q_X ( A_K ) \big ],\hspace{0.05cm}\hspace{0.40cm}{\rm wobei}\hspace{0.15cm} Q_X ( A_i ) = \sum_{ x \in A_i} Q_X ( x )\hspace{0.05cm}. $$
$\text{Please note:}$ The partitioning inequality yields the following size relation with respect to the Kullback-Leibler distances:
- $$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) \hspace{0.25cm}\le \hspace{0.25cm}D(P_X \hspace{0.05cm}\vert \vert \hspace{0.05cm} Q_X) \hspace{0.05cm}.$$
In subtask (1) the Kullback-Leibler distance of the two probability functions $P_X(X)$ and $Q_X(X)$ for $X = \{0,\ 1,\ 2\}$ ⇒ $|X| = 3$ is to be determined.
- Then the setnbsp; $X$ is to be partitioned with $K = 2$ according to
- $A = \{A_1 ,\ A_2\}$ with $A_1 =\{0\}$ and $A_2 = \{ 1,\ 2 \}$ ,
- $B = \{B_1 ,\ B_2\}$ with $B_1 =\{1\}$ and $B_2 = \{ 0,\ 2 \}$,
- $C = \{C_1 ,\ C_2\}$ with $C_1 =\{2\}$ and $C_2 = \{ 0,\ 1\}$,
- Then the respective Kullback-Leibler distances are to be given:
- $D(P_X^{ (A) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (A) } )$,
- $D(P_X^{ (B) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (B) } )$,
- $D(P_X^{ (C) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (C) } )$.
- Finally, subtask (5) asks for the conditions that must be satisfied for the equal sign to be true in the above inequality.
Hints:
- The task belongs to the chapter Some preliminary remarks on 2D random variables.
- In particular, reference is made to the page Informational Divergence – Kullback-Leibler distance.
- The two probability functions can be read from the above graph as follows:
- $$P_X(X) = \big [1/4 , \ 1/2 , \ 1/4 \big ],\hspace{0.5cm} Q_X(X) = \big [1/8, \ 3/4, \ 1/8 \big].$$
Questions
Solution
(1) For the Kullback-Leibler distance holds:
- $$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm}X} P_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)}$$
- $$\Rightarrow D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = \hspace{-0.15cm} \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{3/4} + 2 \cdot \frac{1}{4}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/4}{1/8} = \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{3} + \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} (2) = 1- \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm} \underline {=0.2075\,{\rm (bit)}} \hspace{0.05cm}.$$
(2) With $\text{partition A}$ ⇒ $A_1 = \{0\}$ , $A_2 = \{ 1 , 2 \}$ we get $P_X^{ (A) } (X) = \{1/4 , \ 3/4\}$ and $Q_X^{ (A) } (X) = \{1/8 , \ 7/8\}$. From this follows:
- $$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm}|| \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) = \frac{1}{4}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/4}{1/8} + \frac{3}{4}\cdot {\rm log}_2 \hspace{0.1cm} \frac{3/4}{7/8} =\frac{1}{4}\cdot {\rm log}_2 \hspace{0.1cm} (2) + \frac{3}{4}\cdot {\rm log}_2 \hspace{0.1cm} \frac{6}{7} \hspace{0.15cm} \underline {=0.0832\,{\rm (bit)}} \hspace{0.05cm}.$$
(3) With $\text{partition B}$ ⇒ $B_1 = \{1\}$ , $B_2 = \{ 0 ,\ 2 \}$ the probability functions are $P_X^{ (B) } (X) = \{1/2 , \ 1/2\}$ und $Q_X^{ (B) } (X) = \{3/4 , \ 1/4\}$.
- Analogous to subtask (2) one thus obtains:
- $$D(P_X^{\hspace{0.15cm}(B)} \hspace{0.05cm}|| \hspace{0.05cm} Q_X^{\hspace{0.15cm}(B)}) = \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{3/4} + \frac{1}{2}\cdot {\rm log}_2 \hspace{0.1cm} \frac{1/2}{1/4} \hspace{0.15cm} \underline {=0.2075\,{\rm (bit)}} \hspace{0.05cm}.$$
- The result agrees with that of subtask (1) ⇒ With $\text{partition B}$ the equal sign applies.
(4) With $\text{partition C}$ ⇒ $C_1 = \{2\}$ , $C_2 = \{ 0 , \ 1\}$ one obtains $P_X^{ (C) } (X) = \{1/4, \ 3/4\}$ , $Q_X^{ (C) } (X) = \{1/8, \ 7/8\}$,
i.e. the same functions as for the $\text{partition A}$ ⇒ solution proposal 1.
(5) The $\text{partition C}$ has led to the result $D(P_X^{ (B) } \hspace{0.05cm} || \hspace{0.05cm}Q_X^{ (B) } ) = D(P_X \hspace{0.05cm} || \hspace{0.05cm}Q_X)$ geführt.
- So for this case
- $$\frac{P_X(1)}{Q_X(1)} = \frac{1/2}{3/4} = \frac{2}{3}, \ \frac{P_X(B_1)}{Q_X(B_1)} = \frac{1/2}{3/4} = {2}/{3},$$
- $$\frac{P_X(0)}{Q_X(0)} = \frac{1/4}{1/8} = 2, \ \frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2,$$
- $$\frac{P_X(2)}{Q_X(2)} = \frac{1/4}{1/8} = 2, \ \frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2.$$
- It must therefore hold for all $x \in X$ :
- $$\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_1)}{Q_X(B_1)}, \text{falls } x \in B_1, \hspace{0.5cm}\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_2)}{Q_X(B_2)}, \text{falls } x \in B_2.$$
- By generalisation, one can see that both proposed solutions are correct.