Difference between revisions of "Aufgaben:Exercise 1.6Z: Interpretation of the Frequency Response"
m (Text replacement - "Category:Aufgaben zu Lineare zeitinvariante Systeme" to "Category:Exercises for Linear and Time-Invariant Systems") |
|||
| (20 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
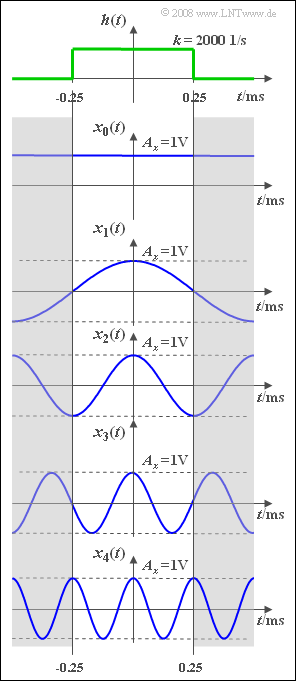
| − | [[File:P_ID862__LZI_Z_1_6.png|right|frame| | + | [[File:P_ID862__LZI_Z_1_6.png|right|frame|Impulse response and input signals]] |
| − | + | The task is meant to investigate the influence of a low-pass filter $H(f)$ on cosinusoidal signals of the form | |
| − | :$$x_i(t) = A_x \cdot {\rm cos}(2\pi f_i t )$$ | + | :$$x_i(t) = A_x \cdot {\rm cos}(2\pi f_i t ).$$ |
| − | + | In the graph you can see the signals $x_i(t)$ where the index $i$ indicates the frequency in $\rm kHz$ . So, $x_2(t)$ describes a $2 \hspace{0.09cm} \rm kHz$–signal. | |
| − | + | The signal amplitude in each case is $A_x = 1 \hspace{0.05cm} \rm V$. The direct (DC) signal $x_0(t)$ is to be interpreted as a limiting case of a cosine signal with frequeny $f_0 =0$. | |
| − | + | The upper sketch shows the rectangular impulse response $h(t)$ of the low-pass filter. Its frequency response is: | |
:$$H(f) = {\rm si}(\pi {f}/{ {\rm \Delta}f}) .$$ | :$$H(f) = {\rm si}(\pi {f}/{ {\rm \Delta}f}) .$$ | ||
| − | + | Due to linearity and the fact that $H(f)$ is real and even the output signals are also cosine-shaped: | |
:$$y_i(t) = A_i \cdot {\rm cos}(2\pi f_i t ) .$$ | :$$y_i(t) = A_i \cdot {\rm cos}(2\pi f_i t ) .$$ | ||
| − | * | + | *The signal amplitudes $A_i$ at the output for different frequencies $f_i$ are searched-for and the solution is to be found in the time domain only. |
| − | * | + | *This somewhat circuitous solution is intended to make the basic relationship between the time and frequency domains clear. |
| Line 25: | Line 25: | ||
| − | '' | + | ''Please note:'' |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. |
| − | * | + | *Contrary to the usual definition of the amplitude, the "$A_i$" may well be negative. Then, this corresponds to the function "minus-cosine". |
| Line 34: | Line 34: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which low-pass filter is at hand here? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Ideal low-pass filter, |
| − | + | + | + slit low-pass filter, |
| − | - | + | - Gaussian low-pass filter. |
| − | { | + | {State the equivalent bandwidth of $H(f)$ . |
|type="{}"} | |type="{}"} | ||
$\Delta f \ =\ $ { 2 3% } $\ \rm kHz$ | $\Delta f \ =\ $ { 2 3% } $\ \rm kHz$ | ||
| − | { | + | {In general, compute the amplitude $A_i$ as a function of $x_i(t)$ and $h(t)$. Which of the following should be considered in the calculations? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + For the cosine signal, $A_i = y_i(t = 0)$ holds. |
| − | - | + | - The following holds: $y_i(t) = x_i(t) · h(t)$. |
| − | + | + | + The following holds: $y_i(t) = x_i(t) ∗ h(t)$. |
| − | { | + | {Which of the following results are true for $A_0, A_2$ and $A_4$ ? The following still holds: $A_i = y_i(t = 0)$. |
|type="[]"} | |type="[]"} | ||
- $A_0 = 0$. | - $A_0 = 0$. | ||
| Line 66: | Line 66: | ||
| − | { | + | {Compute the amplitudes $A_1$ and $A_3$ for a $1 \ \rm kHz$– and $3 \ \rm kHz$–signal. <br>Interpret the results using the spectral functions. |
|type="{}"} | |type="{}"} | ||
$A_1 \ = \ $ { 0.637 5% } $\ \rm V$ | $A_1 \ = \ $ { 0.637 5% } $\ \rm V$ | ||
| Line 73: | Line 73: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Approach 2</u> is correct: It is a <u>slit low-pass filter</u>. |
| − | '''(2)''' | + | '''(2)''' The (equivalent) time duration of the impulse response is $Δt = 0.5 \ \rm ms$. The equivalent bandwidth is equal to the reciprocal: |
:$$Δf = 1/Δt \ \rm \underline{= \ 2 \ kHz}.$$ | :$$Δf = 1/Δt \ \rm \underline{= \ 2 \ kHz}.$$ | ||
| − | '''(3)''' | + | '''(3)''' <u>Approaches 1 and 3</u> are correct: |
| − | * | + | *The amplitude is $A_i = y_i(t = 0)$ since $y_i(t)$ is cosine-shaped. The output signal is calculated by convolution for this purpose: |
:$$A_i = y_i (t=0) = \int\limits_{ - \infty }^{ + \infty } {x_i ( \tau )} \cdot h ( {0 - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | :$$A_i = y_i (t=0) = \int\limits_{ - \infty }^{ + \infty } {x_i ( \tau )} \cdot h ( {0 - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | * | + | *Considering the symmetry and the time limitation of $h(t)$ the following result is obtained: |
:$$A_i = \frac{A_x}{\Delta t} \cdot \int\limits_{ - \Delta t /2 }^{ + \Delta t /2 } {\rm cos}(2\pi f_i \tau )\hspace{0.1cm}{\rm d}\tau.$$ | :$$A_i = \frac{A_x}{\Delta t} \cdot \int\limits_{ - \Delta t /2 }^{ + \Delta t /2 } {\rm cos}(2\pi f_i \tau )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | '''(4)''' | + | '''(4)''' <u>Approaches 2, 3 and 5</u> are correct: |
| − | * | + | *For the direct (DC) signal $x_0(t) = A_x$ , set $f_i = 0$ and one obtains $A_0 = A_x \ \rm \underline{ = \ 1 \hspace{0.05cm} V}$. |
| − | * | + | *In contrast to this, for the cosine frequencies $f_2 = 2 \ \rm kHz$ and $f_4 = 4 \ \rm kHz$ the integral vanishes in each case because then it is integrated over one and two periods, respectively: $A_2 \ \rm \underline{ = \hspace{0.05cm} 0}$ und $A_4 \hspace{0.05cm} \rm \underline{ = \ 0}$. |
| − | * | + | *In the frequency domain, the cases which are dealt with here correspond to: |
:$$H(f=0) = 1, \hspace{0.3cm}H(f=\Delta f) = 0, \hspace{0.3cm}H(f=2\Delta f) = 0.$$ | :$$H(f=0) = 1, \hspace{0.3cm}H(f=\Delta f) = 0, \hspace{0.3cm}H(f=2\Delta f) = 0.$$ | ||
| − | '''(5)''' | + | '''(5)''' The result of subtask '''(3)''' – considering the symmetry – is for $f_i = f_1$: |
:$$A_1= \frac{2A_x}{\Delta t} \cdot \int\limits_{ 0 }^{ \Delta t /2 } {\rm cos}(2\pi f_1 \tau )\hspace{0.1cm}{\rm | :$$A_1= \frac{2A_x}{\Delta t} \cdot \int\limits_{ 0 }^{ \Delta t /2 } {\rm cos}(2\pi f_1 \tau )\hspace{0.1cm}{\rm | ||
d}\tau = \frac{2A_x}{2\pi f_1 \cdot \Delta t} \cdot {\rm sin}(2\pi f_1 \frac{\Delta t}{2} | d}\tau = \frac{2A_x}{2\pi f_1 \cdot \Delta t} \cdot {\rm sin}(2\pi f_1 \frac{\Delta t}{2} | ||
)= A_x \cdot {\rm si}(\pi f_1 \Delta t ).$$ | )= A_x \cdot {\rm si}(\pi f_1 \Delta t ).$$ | ||
| − | * | + | *Taking $f_1 · Δt = 0.5$ into account the result is: |
:$$A_1 = A_x \cdot {\rm si}(\frac{\pi}{2} ) = \frac{2A_x}{\pi} \hspace{0.15cm}\underline{= 0.637\,{\rm V}}.$$ | :$$A_1 = A_x \cdot {\rm si}(\frac{\pi}{2} ) = \frac{2A_x}{\pi} \hspace{0.15cm}\underline{= 0.637\,{\rm V}}.$$ | ||
| − | * | + | *Correspondingly, the following is obtained using $f_3 · Δt = 1.5$: |
:$$A_3 = A_x \cdot {\rm si}({3\pi}/{2} ) = -\frac{2A_x}{3\pi} = -{A_1}/{3}\hspace{0.15cm}\underline{= -0.212\,{\rm V}}.$$ | :$$A_3 = A_x \cdot {\rm si}({3\pi}/{2} ) = -\frac{2A_x}{3\pi} = -{A_1}/{3}\hspace{0.15cm}\underline{= -0.212\,{\rm V}}.$$ | ||
| − | * | + | *The exact same results are obtained – but much faster – by applying the equation: |
:$$A_i = A_x · H(f = f_i).$$ | :$$A_i = A_x · H(f = f_i).$$ | ||
| − | * | + | *From the graphs on the information page it is already obvious that the integral over $x_1(t)$ is positive in the marked area and the integral over $x_3(t)$ is negative. |
| − | * | + | *However, it should be noted that in general amplitude is usually referred to as the magnitude (See notice on the information page). |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 116: | Line 116: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.3 Some Low-Pass Functions in Systems Theory^]] |
Latest revision as of 18:33, 7 September 2021
The task is meant to investigate the influence of a low-pass filter $H(f)$ on cosinusoidal signals of the form
- $$x_i(t) = A_x \cdot {\rm cos}(2\pi f_i t ).$$
In the graph you can see the signals $x_i(t)$ where the index $i$ indicates the frequency in $\rm kHz$ . So, $x_2(t)$ describes a $2 \hspace{0.09cm} \rm kHz$–signal.
The signal amplitude in each case is $A_x = 1 \hspace{0.05cm} \rm V$. The direct (DC) signal $x_0(t)$ is to be interpreted as a limiting case of a cosine signal with frequeny $f_0 =0$.
The upper sketch shows the rectangular impulse response $h(t)$ of the low-pass filter. Its frequency response is:
- $$H(f) = {\rm si}(\pi {f}/{ {\rm \Delta}f}) .$$
Due to linearity and the fact that $H(f)$ is real and even the output signals are also cosine-shaped:
- $$y_i(t) = A_i \cdot {\rm cos}(2\pi f_i t ) .$$
- The signal amplitudes $A_i$ at the output for different frequencies $f_i$ are searched-for and the solution is to be found in the time domain only.
- This somewhat circuitous solution is intended to make the basic relationship between the time and frequency domains clear.
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- Contrary to the usual definition of the amplitude, the "$A_i$" may well be negative. Then, this corresponds to the function "minus-cosine".
Questions
Solution
(2) The (equivalent) time duration of the impulse response is $Δt = 0.5 \ \rm ms$. The equivalent bandwidth is equal to the reciprocal:
- $$Δf = 1/Δt \ \rm \underline{= \ 2 \ kHz}.$$
(3) Approaches 1 and 3 are correct:
- The amplitude is $A_i = y_i(t = 0)$ since $y_i(t)$ is cosine-shaped. The output signal is calculated by convolution for this purpose:
- $$A_i = y_i (t=0) = \int\limits_{ - \infty }^{ + \infty } {x_i ( \tau )} \cdot h ( {0 - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- Considering the symmetry and the time limitation of $h(t)$ the following result is obtained:
- $$A_i = \frac{A_x}{\Delta t} \cdot \int\limits_{ - \Delta t /2 }^{ + \Delta t /2 } {\rm cos}(2\pi f_i \tau )\hspace{0.1cm}{\rm d}\tau.$$
(4) Approaches 2, 3 and 5 are correct:
- For the direct (DC) signal $x_0(t) = A_x$ , set $f_i = 0$ and one obtains $A_0 = A_x \ \rm \underline{ = \ 1 \hspace{0.05cm} V}$.
- In contrast to this, for the cosine frequencies $f_2 = 2 \ \rm kHz$ and $f_4 = 4 \ \rm kHz$ the integral vanishes in each case because then it is integrated over one and two periods, respectively: $A_2 \ \rm \underline{ = \hspace{0.05cm} 0}$ und $A_4 \hspace{0.05cm} \rm \underline{ = \ 0}$.
- In the frequency domain, the cases which are dealt with here correspond to:
- $$H(f=0) = 1, \hspace{0.3cm}H(f=\Delta f) = 0, \hspace{0.3cm}H(f=2\Delta f) = 0.$$
(5) The result of subtask (3) – considering the symmetry – is for $f_i = f_1$:
- $$A_1= \frac{2A_x}{\Delta t} \cdot \int\limits_{ 0 }^{ \Delta t /2 } {\rm cos}(2\pi f_1 \tau )\hspace{0.1cm}{\rm d}\tau = \frac{2A_x}{2\pi f_1 \cdot \Delta t} \cdot {\rm sin}(2\pi f_1 \frac{\Delta t}{2} )= A_x \cdot {\rm si}(\pi f_1 \Delta t ).$$
- Taking $f_1 · Δt = 0.5$ into account the result is:
- $$A_1 = A_x \cdot {\rm si}(\frac{\pi}{2} ) = \frac{2A_x}{\pi} \hspace{0.15cm}\underline{= 0.637\,{\rm V}}.$$
- Correspondingly, the following is obtained using $f_3 · Δt = 1.5$:
- $$A_3 = A_x \cdot {\rm si}({3\pi}/{2} ) = -\frac{2A_x}{3\pi} = -{A_1}/{3}\hspace{0.15cm}\underline{= -0.212\,{\rm V}}.$$
- The exact same results are obtained – but much faster – by applying the equation:
- $$A_i = A_x · H(f = f_i).$$
- From the graphs on the information page it is already obvious that the integral over $x_1(t)$ is positive in the marked area and the integral over $x_3(t)$ is negative.
- However, it should be noted that in general amplitude is usually referred to as the magnitude (See notice on the information page).