Difference between revisions of "Aufgaben:Exercise 5.4: Comparison of Rectangular and Hanning Window"
m (Text replacement - "analyse" to "analyze") |
|||
| Line 11: | Line 11: | ||
Unknown and thus to be estimated are its parameters $A_1$, $f_1$, $A_2$ and $f_2$. | Unknown and thus to be estimated are its parameters $A_1$, $f_1$, $A_2$ and $f_2$. | ||
| − | After weighting the signal with the window function $w(t)$ , the product $y(t) = x(t) \cdot w(t)$ is subjected to a [[Signal_Representation/Discrete_Fourier_Transform_(DFT)|Discrete Fourier Transform]] (DFT) with the parameters $N = 512$ and $T_{\rm P}$. The time $T_{\rm P}$ of the signal section to be | + | After weighting the signal with the window function $w(t)$ , the product $y(t) = x(t) \cdot w(t)$ is subjected to a [[Signal_Representation/Discrete_Fourier_Transform_(DFT)|Discrete Fourier Transform]] (DFT) with the parameters $N = 512$ and $T_{\rm P}$. The time $T_{\rm P}$ of the signal section to be analyzed can be set by the user as desired. |
Two functions are available for windowing, each of which is zero for $|t| > T_{\rm P}/2$: | Two functions are available for windowing, each of which is zero for $|t| > T_{\rm P}/2$: | ||
| Line 50: | Line 50: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
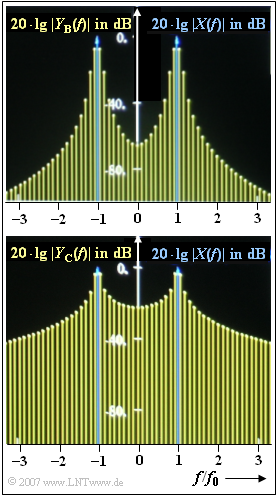
| − | In the graph, two further spectral functions $Y_{\rm B}(f)$ and $Y_{\rm C}(f)$ are shown, which result when a $1 \ \text{kHz}$ signal is | + | In the graph, two further spectral functions $Y_{\rm B}(f)$ and $Y_{\rm C}(f)$ are shown, which result when a $1 \ \text{kHz}$ signal is analyzed by DFT and the DFT parameter $T_{\rm P} = 8.5 \ \text{ms}$ is chosen unfavourably. |
*For one of the images the rectangular window is used, for the other the Hanning window. | *For one of the images the rectangular window is used, for the other the Hanning window. | ||
Revision as of 12:47, 22 September 2021
Let the time course of a periodic signal be given in principle:
- $$x(t) = A_1 \cdot \cos (2 \pi \cdot f_1 \cdot t) + A_2 \cdot \cos (2 \pi \cdot f_2 \cdot t) \hspace{0.05cm}.$$
Unknown and thus to be estimated are its parameters $A_1$, $f_1$, $A_2$ and $f_2$.
After weighting the signal with the window function $w(t)$ , the product $y(t) = x(t) \cdot w(t)$ is subjected to a Discrete Fourier Transform (DFT) with the parameters $N = 512$ and $T_{\rm P}$. The time $T_{\rm P}$ of the signal section to be analyzed can be set by the user as desired.
Two functions are available for windowing, each of which is zero for $|t| > T_{\rm P}/2$:
- The rectangular window:
- $${w} (\nu) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm else} \hspace{0.05cm}, \\ \end{array}$$
- $$W(f) ={1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm},$$
- the Hanning window:
- $${w} (\nu) = \left\{ \begin{array}{c} 0.5 + 0.5 \cdot \cos (2 \pi \cdot {\nu}/{N}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm else} \hspace{0.05cm}, \\ \end{array}$$
- $$W(f) ={0.5}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f}{f_{\rm A}})+ {0.25}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f-f_{\rm A}}{f_{\rm A}})+ {0.5}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$
Here, $W(f)$ is the Fourier transform of the continuous-time window function $w(t)$, while $w(ν)$ indicates the discrete-time weighting function.
In the task, reference is made to various spectral functions $Y(f)$ for example to
- $$Y_{\rm A}(f) = 1\, {\rm V}\cdot {\rm \delta} (f \pm 1\,\,{\rm kHz})+ 0.5\,\, {\rm V}\cdot {\rm \delta} (f \pm 1.125\,\,{\rm kHz}) \hspace{0.05cm}.$$
In the graph, two further spectral functions $Y_{\rm B}(f)$ and $Y_{\rm C}(f)$ are shown, which result when a $1 \ \text{kHz}$ signal is analyzed by DFT and the DFT parameter $T_{\rm P} = 8.5 \ \text{ms}$ is chosen unfavourably.
- For one of the images the rectangular window is used, for the other the Hanning window.
- It is not indicated which graph belongs to which window.
Hints:
- This task belongs to the chapter Spectrum Analysis.
- Note that the frequency resolution $f_{\rm A}$ is equal to the reciprocal of the adjustable parameter $T_{\rm P}$.
- Unfortunately, the indices of $f_{\rm A}$ and $Y_{\rm A}(f)$ collide. It is obvious that they are not related. Just to be on the safe side, we point this out.
Questions
Solution
- Using the Hanning window, three Dirac functions should be recognisable even if $x(t)$ contains only one frequency ⇒ the rectangular window was used.
- With $T_{\rm P} = 4 \ \text{ms}$ , the frequency resolution is $f_{\rm A}= 1/T_{\rm P} = 0.25 \ \text{kHz}$. Thus the frequency $f_2$ does not lie in the given grid and $Y(f)$ would be composed of very many Dirac lines. This means: the third statement is wrong.
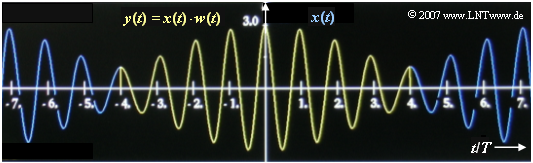
- As can be seen from the graph, $x(t)$ has the period duration $T_{\rm 0} = 8 \ \text{ms}$.
- If one chooses the DFT parameter equal to $T_{\rm P} = 4 \ \text{ms}$ (or an integer multiple thereof), the periodic continuation ${\rm P}\{ x(t)\} $ in the interval $|t| \leq T_{\rm P}/2$ coincides with $x(t)$ , so that the weighting function $w(t)$ has no disturbing effect. So:
- The DFT spectrum $Y(f)$ thus agrees with the actual spectrum.
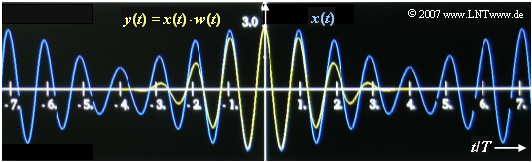
(2) Because of $T_{\rm 0} = 8 \ \text{ms}$ , the Hanning spectrum $W(f)$
- consists of three Dirac functions at positive frequencies
- and three axisymmetrical Diracs at negative frequencies
are composed. For the positive frequencies, the spectral function is:
- $$W(f) =0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm \delta}(f-f_{\rm A})+ 0.25\cdot {\rm \delta}(f+f_{\rm A})\hspace{0.05cm}.$$
The output spectrum results from the convolution between $X(f)$ and $W(f)$. At positive frequencies, there are now four Diracs with the following weights:
- $$\begin{align*} G(f = 0.875\,{\rm kHz}) & = 1\, {\rm V}\cdot 0.25 = 0.250\, {\rm V}, \\ G(f = f_1 = 1.000\,{\rm kHz}) & = 1\, {\rm V}\cdot 0.5 + 0.5\, {\rm V}\cdot 0.25 \hspace{0.15 cm}\underline{ = 0.625\, {\rm V}}, \\ G(f = f_2 = 1.125\,{\rm kHz}) & = 1\, {\rm V}\cdot 0.25 + 0.5\, {\rm V}\cdot 0.5 \hspace{0.15 cm}\underline{= 0.500\, {\rm V}}, \\ G(f = 1.250\,{\rm kHz}) & = 0.5\, {\rm V}\cdot 0.25 = 0.125\, {\rm V} \hspace{0.05cm}.\end{align*}$$
The graph shows the attenuation of the edges by the weighting function $w(t)$ of the Hanning window.
(3) Solution 2 is correct:
- The rectangular window delivers a very strongly distorted result if the window width $T_{\rm P}$ (as here) is not adapted to the cosine frequency.
- In this case, the Hanning window is more suitable. Then the measured spectrum $Y_{\rm B}(f)$ results.
- From the spectrum $Y_{\rm C}(f)$ the searched $1\ \rm kHz$ line is more difficult to detect. The spectrum $Y_{\rm C}(f)$ results after rectangular windowing.