Difference between revisions of "Aufgaben:Exercise 3.15: Data Processing Theorem"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Anwendung auf die Digitalsignalübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multi…“) |
|||
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Application_to_Digital_Signal_Transmission |
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2818__Inf_A_3_14.png|right|frame|"Data Processing Theorem"]] |
| + | We consider the following data processing chain: | ||
| + | * Binary input data $X$ is processed by processor $1$ (top half in the graph) which is describable by conditional probabilities ⇒ $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(\cdot)$ . Its output variable is $Y$. | ||
| + | * A second processor with random variable $Y$ at input and random variable $Z$ at output is given by $P_{Z\hspace{0.03cm}|\hspace{0.03cm}Y}(\cdot)$ (lower half in the graph). $Z$ depends on $Y$ alone (deterministic or stochastic) and is independent of $X$: | ||
| + | :$$P_{Z\hspace{0.05cm}|\hspace{0.03cm} XY\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} x, y) =P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$ | ||
| + | The following nomenclature was used for this description: | ||
| + | :$$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ | ||
| + | The joint probability mass function is: | ||
| + | :$$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.05cm}|\hspace{0.03cm} X\hspace{-0.03cm}}(y\hspace{0.03cm}|\hspace{0.03cm} x)\cdot P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$ | ||
| + | This also means: | ||
| + | $X → Y → Z$ form a [[Theory_of_Stochastic_Signals/Markovketten|Markov chain]]. For such a one, the "Data Processing Theorem" holds with the following consequence: | ||
| + | :$$I(X;Z) \le I(X;Y ) \hspace{0.05cm}, $$ | ||
| + | :$$I(X;Z) \le I(Y;Z ) \hspace{0.05cm}.$$ | ||
| + | The theorem thus states: | ||
| + | :* One cannot gain additional information about input $X$ by manipulating ("processing") data $Y$ . | ||
| + | :* Data processing (by processor $1$) serves only the purpose of making the information contained in $X$ more visible. | ||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The task belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung| Application to Digital Signal Transmission]]. | ||
| + | *Reference is also made to the page [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables#Chain_rule_of_the_mutual_information|Chain rule of the mutual information]] in the previous chapter]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How can the result $I(X; Y) = 1 - H_{\rm bin}(p)$ be interpreted? |
|type="[]"} | |type="[]"} | ||
| − | - | + | + The derivation is based on the properties of a strictly symmetric channel. |
| − | + | - It is exploited that $H_{\rm bin}(p)$ is a concave function. | |
| + | - The result is valid for any probability mass function $P_X(X)$. | ||
| − | { | + | {Which mutual information $I(X; Y)$ results for the first processor with $p = 0.1$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ I(X; Y) \ = \ $ { 0.531 3% } $\ \rm bit$ |
| + | {Which mutual information $I(Y; Z)$ results for the second processor with $q = 0.2$? | ||
| + | |type="{}"} | ||
| + | $I(Y; Z) \ = \ $ { 0.278 3% } $\ \rm bit$ | ||
| + | {Which mutual information $I(X; Z)$ results for the whole system with $p = 0.1$ and $q = 0.2$? | ||
| + | |type="{}"} | ||
| + | $I(X; Z) \ = \ $ { 0.173 3% } $\ \rm bit$ | ||
| + | {Does this example satisfy the "Data Processing Theorem"? | ||
| + | |type="()"} | ||
| + | + Yes, | ||
| + | - No. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Only <u>solution proposal 1</u> is correct: |
| − | '''2 | + | * Both processors describe strictly symmetric channels ⇒ both uniformly dispersive and uniformly focusing. |
| − | '''3 | + | * For such a binary channel, with $Y = \{0, 1\} \ ⇒ \ |Y| = 2$: |
| − | '''4 | + | :$$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{Y\hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \hspace{0.05cm}.$$ |
| − | '''5 | + | *Here it does not matter at all whether one starts from $X = 0$ or from $X = 1$ . |
| − | ''' | + | *For $X = 0$ one obtains with $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 1\hspace{0.03cm}|\hspace{0.03cm}X = 0) = p$ and $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 0\hspace{0.03cm}|\hspace{0.03cm}X = 0) = 1 – p\hspace{0.05cm}$: |
| − | + | :$$ I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm}, | |
| + | \hspace{1.0cm}H_{\rm bin}(p)= p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p}+ (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | ||
| + | *However, the result holds only for $P_X(X) = (0.5, \ 0.5)$ ⇒ maximum mutual information ⇒ channel capacity. | ||
| + | *Otherwise, $I(X; Y)$ is smaller. For example, for $P_X(X) = (1, \ 0)$: $H(X) = 0$ ⇒ $I(X; Y) = 0.$ | ||
| + | *The binary entropy function is concave, but this property was not used in the derivation ⇒ answer 2 is incorrect. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' For processor $1$ , $p = 0.1\hspace{0.05cm}$ gives: | ||
| + | :$$ I(X;Y) = 1 - H_{\rm bin}(0.1) = 1 - 0.469 \hspace{0.15cm} \underline {=0.531 \,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Correspondingly, for the second processor with $q = 0.2\hspace{0.05cm}$: | ||
| + | :$$I(Y;Z) = 1 - H_{\rm bin}(0.2) = 1 - 0.722 \hspace{0.15cm} \underline {=0.278 \,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' The probability for $Z = 0$ under the condition $X = 0$ results in two ways to | ||
| + | :$$P(\hspace{0.01cm}Z\hspace{-0.05cm} = 0\hspace{0.03cm} | \hspace{0.03cm} X\hspace{-0.05cm} = \hspace{-0.05cm}0) = (1-p) \cdot (1-q) + p \cdot q = 1 - p - q + 2pq \stackrel{!}{=} 1 - \varepsilon \hspace{0.05cm}.$$ | ||
| + | *The overall system then has exactly the same BSC structure as processors $1$ and $2$, but now with falsification probability $\varepsilon = p + q - 2pq \hspace{0.05cm}.$ | ||
| + | *For $p = 0.1$ and $q = 0.2$ , we obtain: | ||
| + | :$$ \varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.26) = 1 - 0.827 \hspace{0.15cm} \underline {=0.173 \,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' The answer is <u>YES</u>, because the "Data Processing Theorem" assumes exactly the conditions given here. | ||
| + | |||
| + | However, we want to evaluate some additional numerical results: | ||
| + | * If $0 ≤ p < 0.5$ and $0 ≤ q < 0.5$ hold, we obtain: | ||
| + | :$$\varepsilon = p + q \cdot (1-2p) > p \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(X;Y) \hspace{0.05cm},$$ | ||
| + | :$$\varepsilon = q + p \cdot (1-2q) > q \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(Y;Z) \hspace{0.05cm}.$$ | ||
| + | *For $p = 0.5$ holds independently of $q$, since $I(X; Z)$ cannot be greater than $I(X; Y)$: | ||
| + | :$$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ | ||
| + | *Similarly, with $q = 0.5$ independent of $p$, we obtain: | ||
| + | :$$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ | ||
| + | *Also for $p < 0.5$ and $q > 0.5$ the Data Processing Theorem is not violated, which will be shown here only by an example: | ||
| + | ::With $p = 0.1$ and $q = 0.8$ , the same result is obtained as in subtask '''(4)''': | ||
| + | ::$$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.74) = 1 - H_{\rm bin}(0.26) =0.173 \,{\rm (bit)} \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.3 Application to Digital Signal Transmission^]] |
Latest revision as of 13:22, 24 September 2021
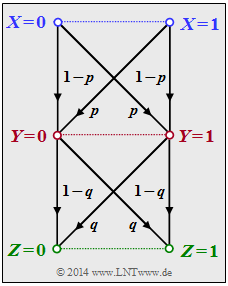
We consider the following data processing chain:
- Binary input data $X$ is processed by processor $1$ (top half in the graph) which is describable by conditional probabilities ⇒ $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(\cdot)$ . Its output variable is $Y$.
- A second processor with random variable $Y$ at input and random variable $Z$ at output is given by $P_{Z\hspace{0.03cm}|\hspace{0.03cm}Y}(\cdot)$ (lower half in the graph). $Z$ depends on $Y$ alone (deterministic or stochastic) and is independent of $X$:
- $$P_{Z\hspace{0.05cm}|\hspace{0.03cm} XY\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} x, y) =P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$
The following nomenclature was used for this description:
- $$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$
The joint probability mass function is:
- $$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.05cm}|\hspace{0.03cm} X\hspace{-0.03cm}}(y\hspace{0.03cm}|\hspace{0.03cm} x)\cdot P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$
This also means:
$X → Y → Z$ form a Markov chain. For such a one, the "Data Processing Theorem" holds with the following consequence:
- $$I(X;Z) \le I(X;Y ) \hspace{0.05cm}, $$
- $$I(X;Z) \le I(Y;Z ) \hspace{0.05cm}.$$
The theorem thus states:
- One cannot gain additional information about input $X$ by manipulating ("processing") data $Y$ .
- Data processing (by processor $1$) serves only the purpose of making the information contained in $X$ more visible.
Hints:
- The task belongs to the chapter Application to Digital Signal Transmission.
- Reference is also made to the page Chain rule of the mutual information in the previous chapter]].
Questions
Solution
(1) Only solution proposal 1 is correct:
- Both processors describe strictly symmetric channels ⇒ both uniformly dispersive and uniformly focusing.
- For such a binary channel, with $Y = \{0, 1\} \ ⇒ \ |Y| = 2$:
- $$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{Y\hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \hspace{0.05cm}.$$
- Here it does not matter at all whether one starts from $X = 0$ or from $X = 1$ .
- For $X = 0$ one obtains with $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 1\hspace{0.03cm}|\hspace{0.03cm}X = 0) = p$ and $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 0\hspace{0.03cm}|\hspace{0.03cm}X = 0) = 1 – p\hspace{0.05cm}$:
- $$ I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm}, \hspace{1.0cm}H_{\rm bin}(p)= p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p}+ (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- However, the result holds only for $P_X(X) = (0.5, \ 0.5)$ ⇒ maximum mutual information ⇒ channel capacity.
- Otherwise, $I(X; Y)$ is smaller. For example, for $P_X(X) = (1, \ 0)$: $H(X) = 0$ ⇒ $I(X; Y) = 0.$
- The binary entropy function is concave, but this property was not used in the derivation ⇒ answer 2 is incorrect.
(2) For processor $1$ , $p = 0.1\hspace{0.05cm}$ gives:
- $$ I(X;Y) = 1 - H_{\rm bin}(0.1) = 1 - 0.469 \hspace{0.15cm} \underline {=0.531 \,{\rm (bit)}} \hspace{0.05cm}.$$
(3) Correspondingly, for the second processor with $q = 0.2\hspace{0.05cm}$:
- $$I(Y;Z) = 1 - H_{\rm bin}(0.2) = 1 - 0.722 \hspace{0.15cm} \underline {=0.278 \,{\rm (bit)}} \hspace{0.05cm}.$$
(4) The probability for $Z = 0$ under the condition $X = 0$ results in two ways to
- $$P(\hspace{0.01cm}Z\hspace{-0.05cm} = 0\hspace{0.03cm} | \hspace{0.03cm} X\hspace{-0.05cm} = \hspace{-0.05cm}0) = (1-p) \cdot (1-q) + p \cdot q = 1 - p - q + 2pq \stackrel{!}{=} 1 - \varepsilon \hspace{0.05cm}.$$
- The overall system then has exactly the same BSC structure as processors $1$ and $2$, but now with falsification probability $\varepsilon = p + q - 2pq \hspace{0.05cm}.$
- For $p = 0.1$ and $q = 0.2$ , we obtain:
- $$ \varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.26) = 1 - 0.827 \hspace{0.15cm} \underline {=0.173 \,{\rm (bit)}} \hspace{0.05cm}.$$
(5) The answer is YES, because the "Data Processing Theorem" assumes exactly the conditions given here.
However, we want to evaluate some additional numerical results:
- If $0 ≤ p < 0.5$ and $0 ≤ q < 0.5$ hold, we obtain:
- $$\varepsilon = p + q \cdot (1-2p) > p \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(X;Y) \hspace{0.05cm},$$
- $$\varepsilon = q + p \cdot (1-2q) > q \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(Y;Z) \hspace{0.05cm}.$$
- For $p = 0.5$ holds independently of $q$, since $I(X; Z)$ cannot be greater than $I(X; Y)$:
- $$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$
- Similarly, with $q = 0.5$ independent of $p$, we obtain:
- $$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$
- Also for $p < 0.5$ and $q > 0.5$ the Data Processing Theorem is not violated, which will be shown here only by an example:
- With $p = 0.1$ and $q = 0.8$ , the same result is obtained as in subtask (4):
- $$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.74) = 1 - H_{\rm bin}(0.26) =0.173 \,{\rm (bit)} \hspace{0.05cm}.$$