Difference between revisions of "Aufgaben:Exercise 3.10Z: BSC Channel Capacity"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Anwendung auf die Digitalsignalübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multi…“) |
|||
| (33 intermediate revisions by 5 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
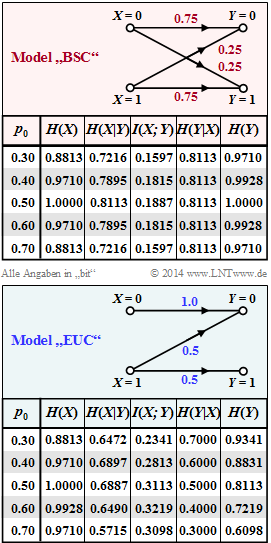
| − | [[File:|right|]] | + | [[File:EN_Inf_Z_3_9_A.png|right|frame|Entropies of "BC" and "BSC"]] |
| + | The channel capacity $C$ was defined by [https://en.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] as the maximum mutual information, whereby the maximization refers solely to the source statistics: | ||
| + | :$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ | ||
| + | In the binary channel with the probability function $P_X(X) = \big [p_0, \ p_1 \big]$ only one parameter is optimizable, for example $p_0$. The probability for a $1$ is thus also fixed: $p_1 = 1 - p_0.$ | ||
| + | The upper graph (reddish background) summarises the results for the [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Channel_capacity_of_a_binary_channel|asymmetric binary channel]] with $ε_0 = 0.01$ and $ε_1 = 0.2$ , which was also considered in the theory section. | ||
| − | === | + | The maximization leads to the result $p_0 = 0.55$ ⇒ $p_1 = 0.45$, and one obtains for the channel capacity: |
| + | :$$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}.$$ | ||
| + | |||
| + | In the lower graph (blue background), the same information-theoretical quantities are given for the [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Symmetric Channel]] $\rm (BSC)$ with the falsification probabilities $ε_0 = ε_1 = ε = 0.1$, which was also assumed for [[Aufgaben:Exercise_3.10:_Mutual_Information_at_the_BSC| Exercise 3.10]]. | ||
| + | |||
| + | In the present exercise you are | ||
| + | :* to analyze the entropies $H(X)$, $H(Y)$, $H(X|Y)$ and $H(Y|X)$, | ||
| + | :* to optimize the source parameter $p_0$ with respect to maximum mutual information $I(X; Y)$ , | ||
| + | :* to determine the channel capacity $C(ε)$ , | ||
| + | :* to give a closed equation for $C(ε)$ by generalization for the BSC channel model $($initially for $ε = 0.1)$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to digital signal transmission]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Application_to_Digital_Signal_Transmission#Channel_capacity_of_a_binary_channel|Channel capacity of a binary channel]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | { Which statements are true for the conditional entropies in the BSC model? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The equivocation results in $H(X|Y) = H_{\rm bin}(ε)$. |
| − | + | + | + The irrelevance results in $H(Y|X) = H_{\rm bin}(ε)$. |
| + | - The irrelevance results in $H(Y|X) = H_{\rm bin}(p_0)$. | ||
| + | {Which statements are true for the channel capacity $C_{\rm BSC}$ of the BSC model? | ||
| + | |type="[]"} | ||
| + | + The channel capacity is equal to the maximum mutual information. | ||
| + | + For the BSC, maximization leads to the result $p_0 = p_1 = 0.5$. | ||
| + | + For $p_0 = p_1 = 0.5$ , $H(X) = H(Y) = 1 \ \rm bit$. | ||
| − | { | + | {Which channel capacity $C_{\rm BSC}$ results depending on the BSC parameter $ε$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ε = 0.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 1 1% } $\ \rm bit$ |
| + | $ε = 0.1\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 0.531 1% } $\ \rm bit$ | ||
| + | $ε = 0.5\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 0. } $\ \rm bit$ | ||
| + | {Which channel capacity $C_{\rm BSC}$ results depending on the BSC parameter $ε$? | ||
| + | |type="{}"} | ||
| + | $ε = 1.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 1 1% } $\ \rm bit$ | ||
| + | $ε = 0.9\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 0.531 1% } $\ \rm bit$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The <u>proposed solution 2</u> is correct, as the following calculation shows: |
| − | '''2 | + | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} $$ |
| − | ''' | + | :$$\Rightarrow \hspace{0.3cm} H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$$ |
| − | ''' | + | *With $p_0 + p_1 = 1$ and the binary entropy function $H_{\rm bin}$, one obtains the proposed result: $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$ |
| − | ''' | + | *For $ε = 0.1$ we get $H(Y|X) = 0.4690 \ \rm bit$. The same value stands for $p_0=0.50$ in the given table. |
| − | ''' | + | *From the table one can also see that for the BSC model (blue background) as well as for the more general (asymmetric) BC model (red background) <br>the equivocation $H(X|Y)$ depends on the source symbol probabilities $p_0$ and $p_1$. It follows that proposed solution 1 cannot be correct. |
| − | ''' | + | *The irrelevance $H(Y|X)$ is independent of the source statistics, so that solution proposal 3 can also be excluded. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>All given alternative solutions</u> are correct: | ||
| + | *The channel capacity is defined as the maximum mutual information, where the maximization has to be done with respect to $P_X = (p_0, p_1)$ : | ||
| + | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | ||
| + | *The equation is generally valid, i.e. also for the unbalanced binary channel highlighted in red. | ||
| + | *The mutual information can be calculated, for example, as $I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$, <br>where according to subtask '''(1)''' the term $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$ is independent of $p_0$ or $p_1 = 1- p_0$ . | ||
| + | *The maximum mutual information thus results exactly when the sink entropy $H(Y)$ is maximum. This is the case for $p_0 = p_1 = 0.5$: | ||
| + | :$$H(X) = H(Y) = 1 \ \rm bit.$$ | ||
| + | |||
| + | |||
| + | |||
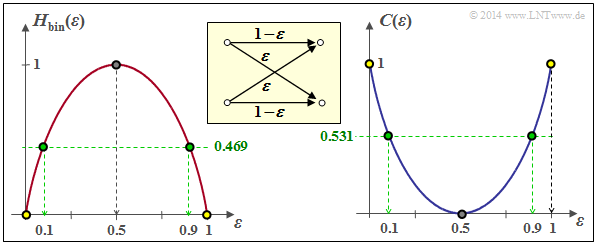
| + | [[File:P_ID2790__Inf_Z_3_9_B.png|frame|Binary entropy function and BSC channel capacity]] | ||
| + | '''(3)''' According to the subtasks '''(1)''' and '''(2)''' one obtains for the BSC channel capacity: | ||
| + | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | ||
| + | |||
| + | The graph shows the binary entropy function on the left and the channel capacity on the right. One obtains: | ||
| + | * for $ε = 0.0$ (error-free channel): <br> $C = 1\ \rm (bit)$ ⇒ dot with yellow filling, | ||
| + | * for $ε = 0.1$ (considered so far): <br> $C = 0.531\ \rm (bit)$ ⇒ dot with green filling, | ||
| + | * for $ε = 0.5$ (completely disturbed): <br> $C = 0\ \rm (bit)$ ⇒ dot with grey filling. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' From the graph one can see that from an information-theoretical point of view $ε = 1$ is identical to $ε = 0$ : | ||
| + | :$$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}1} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0} \hspace{0.15cm} \underline {=1\,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | *The channel only carries out a renaming here. This is called "mapping". | ||
| + | *Every $0$ becomes a $1$ and every $1$ becomes a $0$. Accordingly: | ||
| + | :$$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.9} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.1} \hspace{0.15cm} \underline {=0.531\,{\rm (bit)}} \hspace{0.05cm}$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.3 Application to Digital Signal Transmission^]] |
Latest revision as of 16:07, 27 September 2021
The channel capacity $C$ was defined by Claude E. Shannon as the maximum mutual information, whereby the maximization refers solely to the source statistics:
- $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$
In the binary channel with the probability function $P_X(X) = \big [p_0, \ p_1 \big]$ only one parameter is optimizable, for example $p_0$. The probability for a $1$ is thus also fixed: $p_1 = 1 - p_0.$
The upper graph (reddish background) summarises the results for the asymmetric binary channel with $ε_0 = 0.01$ and $ε_1 = 0.2$ , which was also considered in the theory section.
The maximization leads to the result $p_0 = 0.55$ ⇒ $p_1 = 0.45$, and one obtains for the channel capacity:
- $$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}.$$
In the lower graph (blue background), the same information-theoretical quantities are given for the Binary Symmetric Channel $\rm (BSC)$ with the falsification probabilities $ε_0 = ε_1 = ε = 0.1$, which was also assumed for Exercise 3.10.
In the present exercise you are
- to analyze the entropies $H(X)$, $H(Y)$, $H(X|Y)$ and $H(Y|X)$,
- to optimize the source parameter $p_0$ with respect to maximum mutual information $I(X; Y)$ ,
- to determine the channel capacity $C(ε)$ ,
- to give a closed equation for $C(ε)$ by generalization for the BSC channel model $($initially for $ε = 0.1)$.
Hints:
- The exercise belongs to the chapter Application to digital signal transmission.
- Reference is made in particular to the page Channel capacity of a binary channel.
Questions
Solution
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} $$
- $$\Rightarrow \hspace{0.3cm} H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$$
- With $p_0 + p_1 = 1$ and the binary entropy function $H_{\rm bin}$, one obtains the proposed result: $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$
- For $ε = 0.1$ we get $H(Y|X) = 0.4690 \ \rm bit$. The same value stands for $p_0=0.50$ in the given table.
- From the table one can also see that for the BSC model (blue background) as well as for the more general (asymmetric) BC model (red background)
the equivocation $H(X|Y)$ depends on the source symbol probabilities $p_0$ and $p_1$. It follows that proposed solution 1 cannot be correct. - The irrelevance $H(Y|X)$ is independent of the source statistics, so that solution proposal 3 can also be excluded.
(2) All given alternative solutions are correct:
- The channel capacity is defined as the maximum mutual information, where the maximization has to be done with respect to $P_X = (p_0, p_1)$ :
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
- The equation is generally valid, i.e. also for the unbalanced binary channel highlighted in red.
- The mutual information can be calculated, for example, as $I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$,
where according to subtask (1) the term $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$ is independent of $p_0$ or $p_1 = 1- p_0$ . - The maximum mutual information thus results exactly when the sink entropy $H(Y)$ is maximum. This is the case for $p_0 = p_1 = 0.5$:
- $$H(X) = H(Y) = 1 \ \rm bit.$$
(3) According to the subtasks (1) and (2) one obtains for the BSC channel capacity:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
The graph shows the binary entropy function on the left and the channel capacity on the right. One obtains:
- for $ε = 0.0$ (error-free channel):
$C = 1\ \rm (bit)$ ⇒ dot with yellow filling, - for $ε = 0.1$ (considered so far):
$C = 0.531\ \rm (bit)$ ⇒ dot with green filling, - for $ε = 0.5$ (completely disturbed):
$C = 0\ \rm (bit)$ ⇒ dot with grey filling.
(4) From the graph one can see that from an information-theoretical point of view $ε = 1$ is identical to $ε = 0$ :
- $$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}1} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0} \hspace{0.15cm} \underline {=1\,{\rm (bit)}} \hspace{0.05cm}.$$
- The channel only carries out a renaming here. This is called "mapping".
- Every $0$ becomes a $1$ and every $1$ becomes a $0$. Accordingly:
- $$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.9} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.1} \hspace{0.15cm} \underline {=0.531\,{\rm (bit)}} \hspace{0.05cm}$$