Difference between revisions of "Aufgaben:Exercise 3.1Z: Hilbert Transform"
| (5 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
[[File:P_ID1756__LZI_Z_3_1.png|right|frame|Considered impulse responses]] | [[File:P_ID1756__LZI_Z_3_1.png|right|frame|Considered impulse responses]] | ||
| − | The relation between the real and the imaginary part of the transfer function of realizable causal systems is described by the Hilbert transformation. Here, the following holds: | + | The relation between the real part and the imaginary part of the transfer function of realizable causal systems is described by the Hilbert transformation. Here, the following holds: |
:$${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ | :$${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ | ||
+\infty} | +\infty} | ||
| Line 19: | Line 19: | ||
{\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | ||
| − | Since the transformation and its inverse differ only by the sign, one equation is sufficient. Here, the following applies: | + | Since the transformation and its inverse differ only by the sign, one equation is sufficient. Here, the following applies: |
* To compute the operand marked by the arrow the positive sign is used. | * To compute the operand marked by the arrow the positive sign is used. | ||
| − | * In contrast to this, the minus sign is taken into account for the computation of the operand marked by the circle. | + | * In contrast to this, the minus sign is taken into account for the computation of the operand marked by the circle. |
| − | The Hilbert transformation pertains much more generally than only to the case of application described here. For example, it is also used to determine the (complex) analytical signal corresponding to a real band-pass signal. | + | The Hilbert transformation pertains much more generally than only to the case of application described here. For example, it is also used to determine the (complex) analytical signal corresponding to a real band-pass signal. |
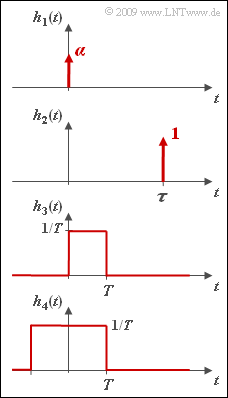
| − | In this exercise, the corresponding frequency responses $H(f)$ are to be determined for the causal impulse responses $h(t)$ given in the diagram according to the inverse Fourier transformation. | + | In this exercise, the corresponding frequency responses $H(f)$ are to be determined for the causal impulse responses $h(t)$ given in the diagram according to the inverse Fourier transformation. |
| − | If $H(f)$ is decomposed into | + | If $H(f)$ is decomposed into real and imaginary parts respectively, then Hilbert correspondences can be derived from it. |
| Line 37: | Line 37: | ||
| − | + | Please note: | |
| − | |||
| − | |||
| − | |||
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem|Conclusions from the Allocation Theorem]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem|Conclusions from the Allocation Theorem]]. | ||
| − | *In particular, reference is made to the theory page [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem# | + | *In particular, reference is made to the theory page [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Hilbert_transform|Hilbert transform]]. |
| Line 80: | Line 77: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The <u>second proposed solution</u> is correct: | + | '''(1)''' The <u>second proposed solution</u> is correct: |
*The Fourier transform of $h_1(t) = \alpha \cdot \delta(t)$ is: | *The Fourier transform of $h_1(t) = \alpha \cdot \delta(t)$ is: | ||
:$$H_1(f) = \alpha \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re} \left\{ H_1(f) \right \} = \alpha , | :$$H_1(f) = \alpha \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re} \left\{ H_1(f) \right \} = \alpha , | ||
| Line 87: | Line 84: | ||
| − | '''(2)''' The <u>last proposed solution</u> is correct: | + | '''(2)''' The <u>last proposed solution</u> is correct: |
| − | *The following frequency response is obtained for the impulse response $h_2(t)$ considering the [[Signal_Representation/Fourier_Transform_Theorems#Shifting Theorem|shifting theorem]] and | + | *The following frequency response is obtained for the impulse response $h_2(t)$ considering the [[Signal_Representation/Fourier_Transform_Theorems#Shifting Theorem|shifting theorem]] and [[Signal_Representation/Calculating_With_Complex_Numbers#Representation by magnitude and phase|Euler's theorem]] : |
:$$H_2(f) ={\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f \tau} = \cos (2\pi | :$$H_2(f) ={\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f \tau} = \cos (2\pi | ||
f \tau) - {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi | f \tau) - {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi | ||
| Line 104: | Line 101: | ||
| − | '''(3)''' <u>Both proposed solutions</u> are correct: | + | '''(3)''' <u>Both proposed solutions</u> are correct: |
*For the rectangular impulse response $h_3(t)$ of width $T$ and height $1/T$ the spectral function is obtained according to the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_first_Fourier_integral|first Fourier integral]]: | *For the rectangular impulse response $h_3(t)$ of width $T$ and height $1/T$ the spectral function is obtained according to the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_first_Fourier_integral|first Fourier integral]]: | ||
:$$H_3(f) = \int_{-\infty}^{ | :$$H_3(f) = \int_{-\infty}^{ | ||
| Line 121: | Line 118: | ||
T}}{{\rm j}\cdot 2\pi f T} \hspace{0.05cm}.$$ | T}}{{\rm j}\cdot 2\pi f T} \hspace{0.05cm}.$$ | ||
| − | *Using | + | *Using [[Signal_Representation/Calculating_With_Complex_Numbers#Representation by magnitude and phase|Euler's theorem]] this can also be rewritten as follows: |
:$$H_3(f) = \frac{1-\cos (2\pi | :$$H_3(f) = \frac{1-\cos (2\pi | ||
f T) + {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f | f T) + {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f | ||
Latest revision as of 16:45, 9 October 2021
The relation between the real part and the imaginary part of the transfer function of realizable causal systems is described by the Hilbert transformation. Here, the following holds:
- $${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ +\infty} { \frac{{\rm Re} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm},$$
- $${\rm Re} \left\{ H(f) \right \} = \frac{1}{\pi }\int_{-\infty}^{ +\infty} { \frac{{\rm Im} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
The following is used as a common abbreviation for these two integral transformations:
- $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$
Since the transformation and its inverse differ only by the sign, one equation is sufficient. Here, the following applies:
- To compute the operand marked by the arrow the positive sign is used.
- In contrast to this, the minus sign is taken into account for the computation of the operand marked by the circle.
The Hilbert transformation pertains much more generally than only to the case of application described here. For example, it is also used to determine the (complex) analytical signal corresponding to a real band-pass signal.
In this exercise, the corresponding frequency responses $H(f)$ are to be determined for the causal impulse responses $h(t)$ given in the diagram according to the inverse Fourier transformation.
If $H(f)$ is decomposed into real and imaginary parts respectively, then Hilbert correspondences can be derived from it.
Please note:
- The exercise belongs to the chapter Conclusions from the Allocation Theorem.
- In particular, reference is made to the theory page Hilbert transform.
Questions
Solution
- The Fourier transform of $h_1(t) = \alpha \cdot \delta(t)$ is:
- $$H_1(f) = \alpha \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re} \left\{ H_1(f) \right \} = \alpha , \hspace{0.2cm}{\rm Im} \left\{ H_1(f) \right \} = 0\hspace{0.05cm}.$$
(2) The last proposed solution is correct:
- The following frequency response is obtained for the impulse response $h_2(t)$ considering the shifting theorem and Euler's theorem :
- $$H_2(f) ={\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f \tau} = \cos (2\pi f \tau) - {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f \tau)\hspace{0.05cm}.$$
- This results in the Hilbert correspondence
- $$\cos (2\pi f \tau) \hspace{0.3cm} \leftarrow\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.3cm} -\sin (2\pi f \tau)\hspace{0.7cm}{\rm or}\hspace{0.7cm} \cos (2\pi f \tau) \hspace{0.3cm} \bullet\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!-\!\hspace{-0.1cm}\rightarrow\hspace{0.3cm} \sin (2\pi f \tau) \hspace{0.05cm}.$$
(3) Both proposed solutions are correct:
- For the rectangular impulse response $h_3(t)$ of width $T$ and height $1/T$ the spectral function is obtained according to the first Fourier integral:
- $$H_3(f) = \int_{-\infty}^{ +\infty} { h_3(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t \hspace{0.05cm} = \frac{1}{T} \cdot \int_{0}^{ T} { {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t = \left [\frac{1}{-{\rm j}\cdot 2\pi f T} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} t} \right ]_{0}^{T} = \frac{1-{\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} T}}{{\rm j}\cdot 2\pi f T} \hspace{0.05cm}.$$
- Using Euler's theorem this can also be rewritten as follows:
- $$H_3(f) = \frac{1-\cos (2\pi f T) + {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f T)}{{\rm j}\cdot 2\pi f T} = \frac{\sin (2\pi f T)}{ 2\pi f T} - {\rm j}\cdot \frac{1 - \cos (2\pi f T)}{ 2\pi f T}\hspace{0.05cm}.$$
- Furthermore, the following holds considering the transformation $1 - \cos(\alpha) = 2 \cdot \sin^2(\alpha/2)$:
- $${\rm Re}\hspace{-0.05cm} \left\{ H_3(f) \right \} = {\rm si} (2\pi f T)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x \hspace{0.05cm}, \hspace{0.5cm} {\rm Im} \hspace{-0.05cm}\left\{ H_3(f) \right \} = -\frac{\sin^2 (\pi f T)}{ \pi f T}= - {\rm si} (\pi f T) \cdot {\rm sin} (\pi f T) \hspace{0.05cm}.$$
(4) No is correct:
- The impulse response $h_4(t)$ is not causal so that no Hilbert correspondence can be derived from the associated Fourier spectrum $H_4(f)$ .