Difference between revisions of "Aufgaben:Exercise 3.2: Laplace Transform"
| (10 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
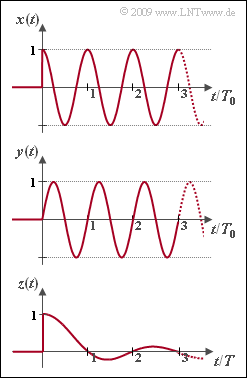
[[File:P_ID1763__LZI_A_3_2.png|right|frame|Three causal time functions]] | [[File:P_ID1763__LZI_A_3_2.png|right|frame|Three causal time functions]] | ||
| − | + | Causal signals and systems are usually described by means of the Laplace transformation. If $x(t)$ is identical to zero for all times $t < 0$, then the Laplace transform is: | |
:$$X_{\rm L}(p) = \int_{0}^{ | :$$X_{\rm L}(p) = \int_{0}^{ | ||
\infty} | \infty} | ||
| Line 10: | Line 10: | ||
d}t\hspace{0.05cm}\hspace{0.05cm} .$$ | d}t\hspace{0.05cm}\hspace{0.05cm} .$$ | ||
| − | In | + | In this exercise, the Laplace transforms of the causal signals shown in the graph are to be determined. The following equations are valid in each case only for $t \ge 0$. For negative times, all signals are identical to zero. |
| − | * | + | *Cosine signal with period $T_0$: |
:$$x(t) = {\rm cos} (2\pi \cdot {t}/{T_0})= {\rm cos} (\omega_0 \cdot t) \hspace{0.05cm},$$ | :$$x(t) = {\rm cos} (2\pi \cdot {t}/{T_0})= {\rm cos} (\omega_0 \cdot t) \hspace{0.05cm},$$ | ||
| − | * | + | *sine signal with period $T_0$: |
:$$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$ | :$$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$ | ||
| − | *$\sin(t)/t$– | + | *$\sin(t)/t$–signal with equivalent zero-crossings at a distance of $T$: |
| − | :$$z(t) = {\rm si} (\pi \cdot {t}/{T})\hspace{0. | + | :$$z(t) = {\rm si} (\pi \cdot {t}/{T})= {\rm sinc} ({t}/{T})\hspace{0.4cm}{\rm with}\hspace{0.4cm}{\rm si}(x)= {\rm sin}(x)/x ={\rm sinc}(x)/\pi \hspace{0.05cm}.$$ |
| − | |||
| − | + | The following equation can'''<u>not</u>''' be used to calculate the spectral function since $z(t)$ is not energy-limited just as the signals $x(t)$ and $y(t)$ : | |
:$$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it | :$$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it | ||
f}} .$$ | f}} .$$ | ||
| − | + | Rather, the fact that $z(t) = s(t) \cdot \gamma(t)$ holds is to be considered where $s(t)$ denotes the conventional symmetric $\rm si$–function here: | |
:$$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad | :$$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad | ||
| − | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f)$$ | + | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f).$$ |
| − | $S(f)$ | + | $S(f)$ is a rectangular function symmetric about $f = 0$ with height $T$ and width $1/T$. |
| − | + | The Fourier transform of the step function $\gamma(t)$ is: | |
:$$\gamma(t) \quad | :$$\gamma(t) \quad | ||
\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad {\it \Gamma}(f) = {1}/{2} | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad {\it \Gamma}(f) = {1}/{2} | ||
\cdot \delta (f) + \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$ | \cdot \delta (f) + \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 48: | Line 41: | ||
''Please note:'' | ''Please note:'' | ||
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|Laplace Transform and p-Transfer Function]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|Laplace Transform and p-Transfer Function]]. | ||
| − | * | + | * In the sample solution, we use of the two comparable functions ${\rm si}(x)$ and ${\rm sinc}(x)$ the former. |
| + | *The following definite integrals are given: | ||
:$$\int_{0}^{ | :$$\int_{0}^{ | ||
\infty} | \infty} | ||
| Line 71: | Line 65: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the Laplace transform $X_{\rm L}(p)$ of the causal cosine function $x(t)$. What is the correct solution? |
|type="()"} | |type="()"} | ||
- $X_{\rm L}(p) = \omega_0/(p^2 + \omega_0^2)$. | - $X_{\rm L}(p) = \omega_0/(p^2 + \omega_0^2)$. | ||
| Line 77: | Line 71: | ||
- $X_{\rm L}(p) = 1/(p^2 + \omega_0^2)$. | - $X_{\rm L}(p) = 1/(p^2 + \omega_0^2)$. | ||
| − | { | + | {Compute the Laplace transform $Y_{\rm L}(p)$ of the causal sine function $y(t)$. What is the correct solution? |
|type="()"} | |type="()"} | ||
+ $Y_{\rm L}(p) = \omega_0/(p^2 + \omega_0^2)$. | + $Y_{\rm L}(p) = \omega_0/(p^2 + \omega_0^2)$. | ||
| Line 84: | Line 78: | ||
| − | { | + | {Compute the Laplace transform $Z_{\rm L}(p)$ of the causal $\rm si$–function $z(t)$. What is the correct solution? |
|type="()"} | |type="()"} | ||
| − | - $Z_{\rm L}(p)$ | + | - $Z_{\rm L}(p)$ has a rectangular shape. |
- $Z_{\rm L}(p) = \arctan (1/p)$. | - $Z_{\rm L}(p) = \arctan (1/p)$. | ||
+ $Z_{\rm L}(p) = T/\pi \cdot \arctan (\pi/(pT))$. | + $Z_{\rm L}(p) = T/\pi \cdot \arctan (\pi/(pT))$. | ||
| − | { | + | {Compute the real part of the spectrum $Z(f)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + ${\rm Re}\big[Z(f)\big]$ | + | + ${\rm Re}\big[Z(f)\big]$ has a rectangular shape. |
| − | - ${\rm Re}\big[Z(f)\big]$ | + | - ${\rm Re}\big[Z(f)\big]$ is proportional to $\ln\; \big|(f \cdot T -0.5)/(f \cdot T +0.5)\big|.$ |
| − | { | + | {Compute the imaginary part of $Z(f)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - ${\rm Im}\big[Z(f)\big]$ | + | - ${\rm Im}\big[Z(f)\big]$ has a rectangular shape. |
| − | + ${\rm Im}\big[Z(f)\big]$ | + | + ${\rm Im}\big[Z(f)\big]$ is proportional to $\ln\; \big|(f \cdot T -0.5)/(f \cdot T +0.5)\big|.$ |
| Line 109: | Line 103: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Suggested solution 2</u> is correct: |
| − | * | + | *According to the Laplace definition, the following holds with the given equations: |
:$$X_{\rm L}(p) = \int_{0}^{ | :$$X_{\rm L}(p) = \int_{0}^{ | ||
\infty} | \infty} | ||
| Line 119: | Line 113: | ||
d}t = \frac{p}{p^2 + \omega_0^2} | d}t = \frac{p}{p^2 + \omega_0^2} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *Suggestion 3 is ruled out since $X_{\rm L}(p)$ must have the unit "second" (integral over time) while $p$ and $\omega_0$ each have the unit "1/s". |
| − | '''(2)''' | + | '''(2)''' <u>Suggested solution 1</u> is correct: |
| − | * | + | *Here, the following holds using the same approach as in the subtask '''(1)''': |
:$$Y_{\rm L}(p) = \int_{0}^{ | :$$Y_{\rm L}(p) = \int_{0}^{ | ||
\infty} | \infty} | ||
| Line 133: | Line 127: | ||
| − | '''(3)''' | + | '''(3)''' <u>Suggested solution 3</u> is correct: |
| − | * | + | *The $p$–transfer function of the causal $\rm si$–function is as follows considering the integral given above: |
:$$Z_{\rm L}(p) = \int_{0}^{ | :$$Z_{\rm L}(p) = \int_{0}^{ | ||
\infty} | \infty} | ||
| Line 140: | Line 134: | ||
d}t = \frac{T}{\pi} \cdot {\rm arctan} \; \frac{\pi}{p\cdot T} | d}t = \frac{T}{\pi} \cdot {\rm arctan} \; \frac{\pi}{p\cdot T} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *Suggestion 1 only applies to the Fourier transform of the non-causal $\rm si$–function. |
| − | * | + | *Since here the argument of the $\rm arctan$ function is dimensional, suggestion 2 cannot be true for this reason alone. |
| − | '''(4)''' | + | '''(4)''' <u>Suggested solution 1</u> is correct: |
| − | * | + | *The following arises as a result from $z(t) = s(t) \cdot \gamma(t)$ with the convolution theorem: |
:$$Z(f) = S(f) \star {\it \Gamma}(f) = {1}/{2} | :$$Z(f) = S(f) \star {\it \Gamma}(f) = {1}/{2} | ||
\cdot S(f) \star \delta (f) + S(f) \star \frac{1}{{\rm j} \cdot | \cdot S(f) \star \delta (f) + S(f) \star \frac{1}{{\rm j} \cdot | ||
2\pi f}\hspace{0.05cm}.$$ | 2\pi f}\hspace{0.05cm}.$$ | ||
| − | * | + | *Since $S(f)$ is real, the real part of $Z(f)$ is obtained as the first term of this equation: |
:$${\rm Re}[ Z(f)] = {1}/{2} | :$${\rm Re}[ Z(f)] = {1}/{2} | ||
\cdot S(f) \star \delta (f) = {1}/{2} \cdot S(f) | \cdot S(f) \star \delta (f) = {1}/{2} \cdot S(f) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The real part of $Z(f)$ thus has the same rectangular shape as $S(f)$, but it is only half as high: |
:$${\rm Re}\{ Z(f)\}= \left\{ \begin{array}{c} T/2 \\ | :$${\rm Re}\{ Z(f)\}= \left\{ \begin{array}{c} T/2 \\ | ||
0 \end{array} \right. | 0 \end{array} \right. | ||
| Line 164: | Line 158: | ||
{ |f|> 1/(2T)\hspace{0.05cm},} | { |f|> 1/(2T)\hspace{0.05cm},} | ||
\end{array} | \end{array} | ||
| − | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm | + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm suggestion \hspace{0.15cm} 1}}.$$ |
| − | '''(5)''' | + | '''(5)''' <u>Suggested solution 2</u> is correct: |
| − | * | + | *With the result of the last subtask, it follows for the imaginary part: |
:$${\rm Im}\{ Z(f)\} = S(f) \star \frac{(-1)}{{\rm j} \cdot | :$${\rm Im}\{ Z(f)\} = S(f) \star \frac{(-1)}{{\rm j} \cdot | ||
2\pi f} \hspace{0.05cm}.$$ | 2\pi f} \hspace{0.05cm}.$$ | ||
| − | * | + | *This convolution integral yields the following for sufficiently large frequencies $f \ge 1/(2T)$: |
:$${\rm Im}\{ Z(f)\} = -T \cdot \int_{f- 1/(2T)}^{ | :$${\rm Im}\{ Z(f)\} = -T \cdot \int_{f- 1/(2T)}^{ | ||
f+ 1/(2T)} { \frac{1}{2\pi x}}\hspace{0.1cm}{\rm | f+ 1/(2T)} { \frac{1}{2\pi x}}\hspace{0.1cm}{\rm | ||
d}x = \frac{T}{2\pi } \cdot {\rm ln}\hspace{0.15cm}\left |\frac{f- 1/(2T)}{f+ 1/(2T)}\right | | d}x = \frac{T}{2\pi } \cdot {\rm ln}\hspace{0.15cm}\left |\frac{f- 1/(2T)}{f+ 1/(2T)}\right | | ||
\hspace{0.05cm} | \hspace{0.05cm} | ||
| − | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm | + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm suggestion \hspace{0.15cm} 2}}.$$ |
Latest revision as of 12:44, 13 October 2021
Causal signals and systems are usually described by means of the Laplace transformation. If $x(t)$ is identical to zero for all times $t < 0$, then the Laplace transform is:
- $$X_{\rm L}(p) = \int_{0}^{ \infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}\hspace{0.05cm} .$$
In this exercise, the Laplace transforms of the causal signals shown in the graph are to be determined. The following equations are valid in each case only for $t \ge 0$. For negative times, all signals are identical to zero.
- Cosine signal with period $T_0$:
- $$x(t) = {\rm cos} (2\pi \cdot {t}/{T_0})= {\rm cos} (\omega_0 \cdot t) \hspace{0.05cm},$$
- sine signal with period $T_0$:
- $$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$
- $\sin(t)/t$–signal with equivalent zero-crossings at a distance of $T$:
- $$z(t) = {\rm si} (\pi \cdot {t}/{T})= {\rm sinc} ({t}/{T})\hspace{0.4cm}{\rm with}\hspace{0.4cm}{\rm si}(x)= {\rm sin}(x)/x ={\rm sinc}(x)/\pi \hspace{0.05cm}.$$
The following equation cannot be used to calculate the spectral function since $z(t)$ is not energy-limited just as the signals $x(t)$ and $y(t)$ :
- $$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} .$$
Rather, the fact that $z(t) = s(t) \cdot \gamma(t)$ holds is to be considered where $s(t)$ denotes the conventional symmetric $\rm si$–function here:
- $$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f).$$
$S(f)$ is a rectangular function symmetric about $f = 0$ with height $T$ and width $1/T$.
The Fourier transform of the step function $\gamma(t)$ is:
- $$\gamma(t) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad {\it \Gamma}(f) = {1}/{2} \cdot \delta (f) + \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$
Please note:
- The exercise belongs to the chapter Laplace Transform and p-Transfer Function.
- In the sample solution, we use of the two comparable functions ${\rm si}(x)$ and ${\rm sinc}(x)$ the former.
- The following definite integrals are given:
- $$\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \cos(qx)}\hspace{0.1cm}{\rm d}x = \frac{p}{p^2 + q^2}\hspace{0.05cm} , \hspace{1.0cm}\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \sin(qx)}\hspace{0.1cm}{\rm d}x = \frac{q}{p^2 + q^2}\hspace{0.05cm} , $$
- $$\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \frac{\sin(qx)}{x}}\hspace{0.1cm}{\rm d}x = {\rm arctan}\hspace{0.15cm}\frac{q}{p}\hspace{0.05cm} , \hspace{0.6cm} \int_{A}^{ B} { \frac{1}{x}}\hspace{0.1cm}{\rm d}x = {\rm ln}\hspace{0.15cm}\frac{B}{A}\hspace{0.05cm} .$$
Questions
Solution
- According to the Laplace definition, the following holds with the given equations:
- $$X_{\rm L}(p) = \int_{0}^{ \infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \int\limits_{0}^{ \infty} { {\rm cos} (\omega_0 \cdot T) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \frac{p}{p^2 + \omega_0^2} \hspace{0.05cm} .$$
- Suggestion 3 is ruled out since $X_{\rm L}(p)$ must have the unit "second" (integral over time) while $p$ and $\omega_0$ each have the unit "1/s".
(2) Suggested solution 1 is correct:
- Here, the following holds using the same approach as in the subtask (1):
- $$Y_{\rm L}(p) = \int_{0}^{ \infty} { {\rm sin} (\omega_0 \cdot T) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \frac{\omega_0}{p^2 + \omega_0^2} \hspace{0.05cm} .$$
(3) Suggested solution 3 is correct:
- The $p$–transfer function of the causal $\rm si$–function is as follows considering the integral given above:
- $$Z_{\rm L}(p) = \int_{0}^{ \infty} { \frac{\sin(\pi \cdot t/T)}{\pi \cdot t/T} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \frac{T}{\pi} \cdot {\rm arctan} \; \frac{\pi}{p\cdot T} \hspace{0.05cm} .$$
- Suggestion 1 only applies to the Fourier transform of the non-causal $\rm si$–function.
- Since here the argument of the $\rm arctan$ function is dimensional, suggestion 2 cannot be true for this reason alone.
(4) Suggested solution 1 is correct:
- The following arises as a result from $z(t) = s(t) \cdot \gamma(t)$ with the convolution theorem:
- $$Z(f) = S(f) \star {\it \Gamma}(f) = {1}/{2} \cdot S(f) \star \delta (f) + S(f) \star \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$
- Since $S(f)$ is real, the real part of $Z(f)$ is obtained as the first term of this equation:
- $${\rm Re}[ Z(f)] = {1}/{2} \cdot S(f) \star \delta (f) = {1}/{2} \cdot S(f) \hspace{0.05cm}.$$
- The real part of $Z(f)$ thus has the same rectangular shape as $S(f)$, but it is only half as high:
- $${\rm Re}\{ Z(f)\}= \left\{ \begin{array}{c} T/2 \\ 0 \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array} \begin{array}{*{20}c} { |f|< 1/(2T)\hspace{0.05cm},} \\ { |f|> 1/(2T)\hspace{0.05cm},} \end{array} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm suggestion \hspace{0.15cm} 1}}.$$
(5) Suggested solution 2 is correct:
- With the result of the last subtask, it follows for the imaginary part:
- $${\rm Im}\{ Z(f)\} = S(f) \star \frac{(-1)}{{\rm j} \cdot 2\pi f} \hspace{0.05cm}.$$
- This convolution integral yields the following for sufficiently large frequencies $f \ge 1/(2T)$:
- $${\rm Im}\{ Z(f)\} = -T \cdot \int_{f- 1/(2T)}^{ f+ 1/(2T)} { \frac{1}{2\pi x}}\hspace{0.1cm}{\rm d}x = \frac{T}{2\pi } \cdot {\rm ln}\hspace{0.15cm}\left |\frac{f- 1/(2T)}{f+ 1/(2T)}\right | \hspace{0.05cm} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm suggestion \hspace{0.15cm} 2}}.$$