Aufgaben:Exercise 1.1: Multiplexing in the GSM System

• Return to book

Zum Multiplexing
beim GSM–Mobilfunksystem

The Global System for Mobile Communication (GSM) mobile communications standard, which has been established in Europe since 1992, uses both frequency division and time division multiplexing to enable several users to communicate in one cell.

Some characteristics of the system are given below in somewhat simplified form. A more detailed description can be found in the chapter   General Description of GSM  in the book Buch „Examples of Communication Systems”.

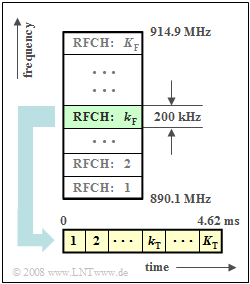
• The frequency band of the uplink (the connection from the mobile to the base station) is between  $\text{890 MHz}$  and $\text{915 MHz}$.  Taking into account the guard bands $($each around $\text{100 kHz)}$  at both ends, a total bandwidth of   $\text{24.8 MHz}$  is thus available for the uplink.
• This band is used by  $K_{\rm F}$  subchannels (Radio Frequency Channels ), which are adjacent in frequency with a respective spacing of   $\text{200 kHz}$  The numbering is done with the running variable  $k_{\rm F}$, starting with  $k_{\rm F} = 1$.
• The frequency range for the downlink (the connection from the base station to the mobile station) is   $\text{45 MHz}$  above the uplink and is structured in exactly the same way as the uplink.
• Each of these FDMA subchannels is used simultaneously by  $K_{\rm T}$  users via TDMA (Time Division Multiple Access).
• A time slot of duration   $T ≈ 577 \rm µ s$  is available to each user at intervals of  $\text{4.62 ms}$ .
• During this time, the (approximate)   $156$  bits describing the voice signal must be transmitted, taking data reduction and channel coding into account.

Hints:

• This exercise belongs to the Chapter  Objectives of Modulation and Demodulation.
• Particular reference is made to the pages
  • Channel bundling – frequency division multiplexing  sowie  
  • Time Division Multiplex methods.

Questions

1

How many partial channels result from frequency division multiplexing?

$K_{\rm F} \ = \ $

2

What is the central frequency  $f_{\rm M}$ of the Radio Frequency Channel  in the uplink with running number  $k_{\rm F} = 100$?

$f_{\rm M} \ = \ $ $\ \rm MHz$

3

Which downlink channel   $($number  $k_{\rm F})$  uses the frequency  $\text{940 MHz}$?

$k_{\rm F} \ = \ $

4

How many partial channels result in the GSM through time division multiplexing?

$K_{\rm T} \ = \ $

5

How many GSM–users can be simultaneously active in one cell?

$K \ = \ $

6

How big is the gross bitrate for GSM?

$R_{\rm Brutto} \ = \ $ $\ \rm kbit/s$

Sample Solution

Solution

(1)  From a total bandwidth of   $\text{24.8 MHz}$  and a channel spacing of 200 kHz folgt

$$K_{\rm F}\hspace{0.15cm}\underline{ = 124}.$$

(2)  The centre frequency of the first channel is   $\text{890.2 MHz}$.  The „RFCH 100” channel is   $\text{ 99 · 200 kHz = 19.8 MHz}$  higher:

$$f_{\rm M}= 890.2 \ \rm MHz + 19.8 \ \rm MHz\hspace{0.15cm}\underline{ = 910 \ \rm MHz}.$$

(3)  To apply the thinking in subtask (2)  , we transfer the task into the uplink: :  

• The same channel with the identifier  $k_{\rm F}$,, which uses the frequency $\text{940 MHz}$  in the downlink, is located at    $\text{895 MHz}$. 
• thus:

$$k_{\rm F} = 1 + \frac {895 \,\,{\rm MHz } - 890.2 \,\,{\rm MHz } }{0.2 \,\,{\rm MHz }} \hspace{0.15cm}\underline {= 25}.$$

(4)  In einem TDMA–Rahmen der Dauer  $\text{4.62}$  Millisekunden können  $K_{\rm T}\hspace{0.15cm}\underline{ = 8}$  Zeitschlitze mit jeweiliger Dauer  $T = 577 \ \rm µ s$  untergebracht werden. 

Anmerkung:  Bei GSM wird tatsächlich  $K_{\rm T} = 8$  verwendet.

(5)  Mit den Ergebnissen der Teilaufgaben  (1)  und  (4)  erhält man:

$$K = K_{\rm F} \cdot K_{\rm T} = 124 \cdot 8 \hspace{0.15cm}\underline {= 992}$$

(6)  Während der Zeit  $T = 577 \ \rm µs$  müssen  $156$  Bit übertragen werden.

• Damit stehen für jedes Bit die Zeit  $T_{\rm B} = 3.699 \ \rm µ s$  zur Verfügung.
• Daraus ergibt sich die (Brutto–)Bitrate

$$R_{\rm Brutto} = \frac {1 }{T_{\rm B}}\hspace{0.15cm}\underline {\approx 270 \,\,{\rm kbit/s }}.$$

• Diese Brutto–Bitrate beinhaltet neben den das Sprachsignal beschreibenden Datensymbolen auch die Trainigssequenz zur Kanalschätzung und die Redundanz für die Kanalcodierung.  Die Netto–Bitrate beträgt beim GSM–System für jeden der acht Benutzer nur etwa  $\text{13 kbit/s}$.