Difference between revisions of "Aufgaben:Exercise 4.Ten: QPSK Channel Capacity"
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Discrete_Input |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_Z_4_10_v2.png|right|frame|Capacity curves for BPSK and QPSK]] |
| − | + | Given are the AWGN channel capacity limit curves for the modulation methods | |
| − | * [[Modulation_Methods/ | + | * [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|Binary Phase Shift Keying]] (BPSK), |
| − | * [[Modulation_Methods/Quadratur–Amplitudenmodulation# | + | * [[Modulation_Methods/Quadratur–Amplitudenmodulation#Other_signal_space_constellations|Quaternary Phase Shift Keying]] (4–PSK or QPSK). |
| − | + | The channel capacities $C_\text{BPSK}$ and $C_\text{QPSK}$ simultaneously indicate the maximum code rate $R_{\rm max}$ , with which the bit error probability $p_\text{B} ≡ 0$ can be asymptotically achieved with BPSK (or QPSK) with suitable channel coding. | |
| − | + | The upper diagram shows the dependence on the parameter $10 \cdot \lg (E_{\rm B}/{N_0})$ in $\rm dB$, where $E_{\rm B}$ indicates the "energy per information bit". | |
| − | * | + | *For large $E_{\rm B}/{N_0}$ values, the BPSK curve provides the maximum code rate $R ≈ 1$. |
| − | * | + | *From the QPSK curve, on the other hand, $R ≈ 2$ can be read. |
| − | + | The capacitance curves for digital input (each with the unit "bit/symbol"), | |
| − | * | + | * green curve ⇒ $C_\text{BPSK} (E_{\rm B}/{N_0})$ and |
| − | * | + | * blue curve ⇒ $C_\text{QPSK} (E_{\rm B}/{N_0})$ |
| − | + | are to be related in subtask '''(3)''' to two Shannon limit curves, each valid for a Gaussian input distribution: | |
:$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\cdot R \cdot E_{\rm B}}{N_0}) ,$$ | :$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\cdot R \cdot E_{\rm B}}{N_0}) ,$$ | ||
:$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$ | :$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$ | ||
| − | + | The two curves simultaneously indicate the maximum code rate $R_{\rm max}$ with which error-free transmission is possible by long channel codes according to the [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Definition_and_meaning_of_channel_capacity|channel coding theorem]] . Of course, different boundary conditions apply to $C_1( E_{\rm B}/{N_0})$ or $C_2( E_{\rm B}/{N_0})$ . Which ones, you shall find out. | |
| − | + | On the other hand, the abscissa in the lower diagram is $10 \cdot \lg (E_{\rm S}/{N_0})$ with the "energy per symbol" $(E_{\rm S})$. Notice that the two limits are not changed from the upper plot:: | |
| − | :$$C_{\rm BPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm BPSK}( E_{\rm B}/{N_0} \to \infty) = 1 \ \rm bit/ | + | :$$C_{\rm BPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm BPSK}( E_{\rm B}/{N_0} \to \infty) = 1 \ \rm bit/symbol,$$ |
| − | :$$C_{\rm QPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm QPSK}( E_{\rm B}/{N_0} \to \infty) = 2 \ \rm bit/ | + | :$$C_{\rm QPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm QPSK}( E_{\rm B}/{N_0} \to \infty) = 2 \ \rm bit/symbol.$$ |
| Line 38: | Line 38: | ||
| − | + | Hints: | |
| − | * | + | *The task belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang|AWGN channel capacity with discrete value input]]. |
| − | * | + | *Reference is made in particular to the page [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#Maximum_code_rate_for_QAM_structures|Maximum code rate for QAM structures]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Do QPSK and 4-QAM differ from an information theoretic point of view? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes. |
| − | + | + | + No. |
| − | { | + | {How can $C_{\rm QPSK}( E_{\rm B}/{N_0})$ be constructed from $C_{\rm BPSK}( E_{\rm B}/{N_0})$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + By doubling: $C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0})$. |
| − | - | + | - Additionally by a shift to the right. |
| − | - | + | - Additionally by a shift to the left. |
| − | - $C_{\rm QPSK}( E_{\rm B}/{N_0})$ | + | - $C_{\rm QPSK}( E_{\rm B}/{N_0})$ cannot be constructed from $C_{\rm BPSK}( E_{\rm B}/{N_0})$ . |
| − | { | + | {What is the relation to the Shannon boundary curves? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $C_{\rm BPSK}( E_{\rm B}/{N_0}) \le C_{\rm 1}( E_{\rm B}/{N_0})$ holds. |
| − | + | + | + $C_{\rm BPSK}( E_{\rm B}/{N_0}) \le C_{\rm 2}( E_{\rm B}/{N_0})$ holds. |
| − | - | + | - $C_{\rm QPSK}( E_{\rm B}/{N_0}) \le C_{\rm 1}( E_{\rm B}/{N_0})$ holds. |
| − | + | + | + $C_{\rm QPSK}( E_{\rm B}/{N_0}) \le C_{\rm 2}( E_{\rm B}/{N_0})$ holds. |
| − | { | + | {How can $C_{\rm QPSK}( E_{\rm S}/{N_0})$ be constructed from $C_{\rm BPSK}( E_{\rm S}/{N_0})$ ? |
| − | |type=" | + | |type="()"} |
| − | + | + | + By doubling: $C_{\rm QPSK}( E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm S}/{N_0})$ and Additionally by a shift to the right. |
| − | + | - By doubling: $C_{\rm QPSK}( E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm S}/{N_0})$ and Additionally by a shift to the left. | |
| − | - | + | - $C_{\rm QPSK}( E_{\rm S}/{N_0})$ cannot be constructed from $C_{\rm BPSK}( E_{\rm S}/{N_0})$ . |
| − | - $C_{\rm QPSK}( E_{\rm S}/{N_0})$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
[[File:P_ID2958__Inf_A_4_10a.png|right|frame|QPSK– und 4–QAM–Signalraumkonstellation]] | [[File:P_ID2958__Inf_A_4_10a.png|right|frame|QPSK– und 4–QAM–Signalraumkonstellation]] | ||
| − | '''(1)''' | + | '''(1)''' The diagram shows the signal space constellations for |
| − | * <i>Quaternary Phase Shift Keying</i> (QPSK), | + | * <i>Quaternary Phase Shift Keying</i> (QPSK), and |
| − | * | + | * four-level quadrature amplitude modulation (4–QAM). |
| − | + | The latter is also referred to as [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Definition_and_meaning_of_channel_capacity|π/4–QPSK]] . Both are identical from an information-theoretic point of view ⇒ <u>answer NO</u>. | |
| − | '''(2)''' | + | '''(2)''' Correct is the <u>proposed solution 1</u>: |
| − | * | + | *The 4–QAM can be viewed as two BPSK constellations in orthogonal planes, where the energy per information bit $(E_{\rm B})$ is the same in both cases. |
| − | * | + | *Since, according to subtask '''(1)''' the 4–QAM is identical to the QSPK, in fact: |
:$$C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0}).$$ | :$$C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0}).$$ | ||
| − | '''(3)''' In | + | '''(3)''' In the lower graph, the two Shannon boundary curves given are sketched together with $C_{\rm BPSK}( E_{\rm B}/{N_0})$ and $C_{\rm QPSK}( E_{\rm B}/{N_0})$ : |
| − | |||
:$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) ,$$ | :$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) ,$$ | ||
:$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$ | :$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$ | ||
| − | [[File: | + | [[File:EN_Inf_Z_4_10c_v2.png|right|frame|Four capacity curves with different statements]] |
| − | + | One can see from this sketch: <u>Proposed solutions 1, 2 and 4</u> are correct. | |
| − | * | + | *The green–dashed curve $C_1( E_{\rm B}/{N_0})$ is valid for the AWGN channel with Gaussian distributed input. |
| − | * | + | *For code rate $R =1$ , $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76\ \rm dB$ is required according to this curve. |
| − | * | + | *For $R =2$ , on the other hand $10 \cdot \lg (E_{\rm B}/{N_0}) = 5.74\ \rm dB$ is required. |
| − | * | + | *The blue–dashed curve $C_2( E_{\rm B}/{N_0})$ gives the Shannon limit for $K=2$ parallel Gaussian channels. Here one needs $10 \cdot \lg (E_{\rm B}/{N_0}) = 0\ \rm dB$ for $R =1$ or $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76\ \rm dB$ for $R =2$. |
| − | * | + | * The one–dimensional BPSK is below $C_1$ in the entire range and thus, of course, below $C_2 > C_1$. |
| − | * | + | * As expected, the two–dimensional QPSK lies below the $C_2$ limit curve relevant for it. However, it is above $C_1$ in the lower range $($up to almost $\text{6 dB)}$ . |
| − | '''(4)''' | + | '''(4)''' The $C_{\rm QPSK}( E_{\rm B}/{N_0})$ curve can also be constructed from $C_{\rm BPSK}( E_{\rm B}/{N_0})$, namely |
| − | * | + | * on the one hand by doubling: |
:$$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) | :$$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$ | 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$ | ||
| − | * | + | * as well as by a shift of $3\ \rm dB$ to the right: |
:$$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) | :$$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) | ||
= | = | ||
2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$ | 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$ | ||
| − | * | + | *The <u>proposed solution 1</u> is correct. This takes into account that with QPSK the energy in one dimension is only $E_{\rm S}/2$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 10:29, 10 November 2021
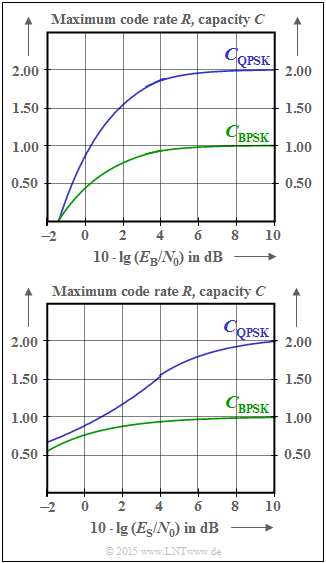
Given are the AWGN channel capacity limit curves for the modulation methods
- Binary Phase Shift Keying (BPSK),
- Quaternary Phase Shift Keying (4–PSK or QPSK).
The channel capacities $C_\text{BPSK}$ and $C_\text{QPSK}$ simultaneously indicate the maximum code rate $R_{\rm max}$ , with which the bit error probability $p_\text{B} ≡ 0$ can be asymptotically achieved with BPSK (or QPSK) with suitable channel coding.
The upper diagram shows the dependence on the parameter $10 \cdot \lg (E_{\rm B}/{N_0})$ in $\rm dB$, where $E_{\rm B}$ indicates the "energy per information bit".
- For large $E_{\rm B}/{N_0}$ values, the BPSK curve provides the maximum code rate $R ≈ 1$.
- From the QPSK curve, on the other hand, $R ≈ 2$ can be read.
The capacitance curves for digital input (each with the unit "bit/symbol"),
- green curve ⇒ $C_\text{BPSK} (E_{\rm B}/{N_0})$ and
- blue curve ⇒ $C_\text{QPSK} (E_{\rm B}/{N_0})$
are to be related in subtask (3) to two Shannon limit curves, each valid for a Gaussian input distribution:
- $$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\cdot R \cdot E_{\rm B}}{N_0}) ,$$
- $$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$
The two curves simultaneously indicate the maximum code rate $R_{\rm max}$ with which error-free transmission is possible by long channel codes according to the channel coding theorem . Of course, different boundary conditions apply to $C_1( E_{\rm B}/{N_0})$ or $C_2( E_{\rm B}/{N_0})$ . Which ones, you shall find out.
On the other hand, the abscissa in the lower diagram is $10 \cdot \lg (E_{\rm S}/{N_0})$ with the "energy per symbol" $(E_{\rm S})$. Notice that the two limits are not changed from the upper plot::
- $$C_{\rm BPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm BPSK}( E_{\rm B}/{N_0} \to \infty) = 1 \ \rm bit/symbol,$$
- $$C_{\rm QPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm QPSK}( E_{\rm B}/{N_0} \to \infty) = 2 \ \rm bit/symbol.$$
Hints:
- The task belongs to the chapter AWGN channel capacity with discrete value input.
- Reference is made in particular to the page Maximum code rate for QAM structures.
Questions
Solution
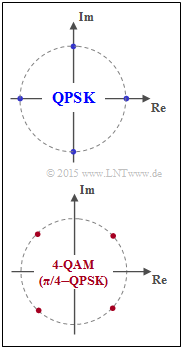
(1) The diagram shows the signal space constellations for
- Quaternary Phase Shift Keying (QPSK), and
- four-level quadrature amplitude modulation (4–QAM).
The latter is also referred to as π/4–QPSK . Both are identical from an information-theoretic point of view ⇒ answer NO.
(2) Correct is the proposed solution 1:
- The 4–QAM can be viewed as two BPSK constellations in orthogonal planes, where the energy per information bit $(E_{\rm B})$ is the same in both cases.
- Since, according to subtask (1) the 4–QAM is identical to the QSPK, in fact:
- $$C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0}).$$
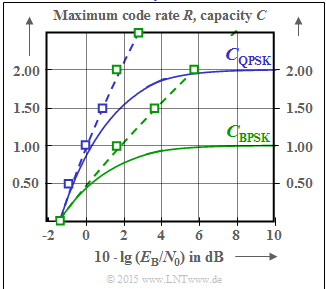
(3) In the lower graph, the two Shannon boundary curves given are sketched together with $C_{\rm BPSK}( E_{\rm B}/{N_0})$ and $C_{\rm QPSK}( E_{\rm B}/{N_0})$ :
- $$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) ,$$
- $$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$
One can see from this sketch: Proposed solutions 1, 2 and 4 are correct.
- The green–dashed curve $C_1( E_{\rm B}/{N_0})$ is valid for the AWGN channel with Gaussian distributed input.
- For code rate $R =1$ , $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76\ \rm dB$ is required according to this curve.
- For $R =2$ , on the other hand $10 \cdot \lg (E_{\rm B}/{N_0}) = 5.74\ \rm dB$ is required.
- The blue–dashed curve $C_2( E_{\rm B}/{N_0})$ gives the Shannon limit for $K=2$ parallel Gaussian channels. Here one needs $10 \cdot \lg (E_{\rm B}/{N_0}) = 0\ \rm dB$ for $R =1$ or $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76\ \rm dB$ for $R =2$.
- The one–dimensional BPSK is below $C_1$ in the entire range and thus, of course, below $C_2 > C_1$.
- As expected, the two–dimensional QPSK lies below the $C_2$ limit curve relevant for it. However, it is above $C_1$ in the lower range $($up to almost $\text{6 dB)}$ .
(4) The $C_{\rm QPSK}( E_{\rm B}/{N_0})$ curve can also be constructed from $C_{\rm BPSK}( E_{\rm B}/{N_0})$, namely
- on the one hand by doubling:
- $$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$
- as well as by a shift of $3\ \rm dB$ to the right:
- $$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$
- The proposed solution 1 is correct. This takes into account that with QPSK the energy in one dimension is only $E_{\rm S}/2$.