Difference between revisions of "Aufgaben:Exercise 1.4Z: Representation of Oscillations"
m |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID969__Mod_Z_1_4.png|right|frame| | + | [[File:P_ID969__Mod_Z_1_4.png|right|frame|Two representations of a harmonic oscillation]] |
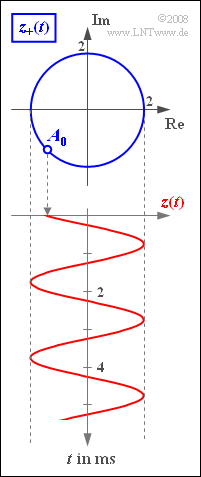
| − | + | Here, we consider a harmonic oscillation $z(t)$, which is shown in the graph together with the corresponding analytical signal $z_+(t)$ . These signals can be described mathematically as follows: | |
:$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm},$$ | :$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm},$$ | ||
:$$ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}$$ | :$$ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}$$ | ||
| − | + | The two amplitude parameters $A_{\rm T} $ and $A_0$ are each dimensionless, the phase value $ϕ_{\rm T} $ is supposed to lie between $\text{±π}$ , and the duration τ $τ$ is non-negative. | |
| − | + | Subtask '''(4)''' refers to the equivalent lowpass signal $z_{\rm TP}(t)$, which is related to $z_+(t)$ as follows: | |
:$$z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}.$$ | :$$z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}.$$ | ||
| − | + | Further note that $ϕ_{\rm T}$ ppears in the above equation with a positive sign. See "Notes on Nomenclature" below for reasons for the differential usage of $φ_{\rm T}$ and $ϕ_{\rm T} = – φ_{\rm T}$. | |
| − | '' | + | ''Notes on Nomenclature:'' |
| − | *In | + | *In this tutorial, as is common in other literature, the phase enters the equations with a negative sign when describing harmonic oscillation, Fourier series, and Fourier integrals, whereas in the context of modulation methods, the phase is always given a plus sign. |
| − | * | + | *To distinguish these two variants, we use $\phi_{\rm T}$ and $\varphi_{\rm T} = - \phi_{\rm T}$. Both symbols denote the lowercase Greek "phi", with the notation $\phi$ used predominantly in Anglo-American contexts, and $\varphi$ in German. |
| − | * | + | *The phase values $\varphi_{\rm T} = 90^\circ$ and $\phi_{\rm T} = -90^\circ$ are thus equivalent and both represent the sine function: |
:$$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi_{\rm T}) = \cos(2 \pi f_0 t + \phi_{\rm T}) = \sin(2 \pi f_0 t ).$$ | :$$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi_{\rm T}) = \cos(2 \pi f_0 t + \phi_{\rm T}) = \sin(2 \pi f_0 t ).$$ | ||
| Line 27: | Line 27: | ||
| − | '' | + | ''Further hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Allgemeines_Modell_der_Modulation|General Model of Modulation]]. |
| − | * | + | *Particular reference is made to the page [[Modulation_Methods/Allgemeines_Modell_der_Modulation#Beschreibung_des_physikalischen_Signals_mit_Hilfe_des_.C3.A4quivalenten_TP-Signals|Describing the physical signal using the equivalent lowpass signal]]. |
| − | * | + | *Further information on this topic can be found in the following chapters of the book "Signal Representation": |
| − | ::(1) [[ Signal_Representation/Harmonic_Oscillation| | + | ::(1) [[ Signal_Representation/Harmonic_Oscillation|Harmonic Oscillation]], |
| − | ::(2) [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function| | + | ::(2) [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function|Analytical Signal and its Spectral Function]] and |
| − | ::(3) [[Signal_Representation/Equivalent_Low_Pass_Signal_and_Its_Spectral_Function| | + | ::(3) [[Signal_Representation/Equivalent_Low_Pass_Signal_and_Its_Spectral_Function| Equivalent Low-Pass Signal and its Spectral Function]]. |
| − | *In | + | *In our tutorial $\rm LNTwww$, the representation of the analytical signal $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{\rm TP}(t)$ angibt. Wir verweisen auf die entsprechenden interaktiven Applets |
::(1) [[Applets:Physikalisches_Signal_%26_Analytisches_Signal|Physikalisches Signal & Analytisches Signal ]], | ::(1) [[Applets:Physikalisches_Signal_%26_Analytisches_Signal|Physikalisches Signal & Analytisches Signal ]], | ||
::(2) [[Applets:Physikalisches_Signal_%26_Äquivalentes_TP-Signal|Physikalisches Signal & Äquivalentes TP-Signal]]. | ::(2) [[Applets:Physikalisches_Signal_%26_Äquivalentes_TP-Signal|Physikalisches Signal & Äquivalentes TP-Signal]]. | ||
Revision as of 18:11, 11 November 2021
Here, we consider a harmonic oscillation $z(t)$, which is shown in the graph together with the corresponding analytical signal $z_+(t)$ . These signals can be described mathematically as follows:
- $$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm},$$
- $$ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}$$
The two amplitude parameters $A_{\rm T} $ and $A_0$ are each dimensionless, the phase value $ϕ_{\rm T} $ is supposed to lie between $\text{±π}$ , and the duration τ $τ$ is non-negative.
Subtask (4) refers to the equivalent lowpass signal $z_{\rm TP}(t)$, which is related to $z_+(t)$ as follows:
- $$z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}.$$
Further note that $ϕ_{\rm T}$ ppears in the above equation with a positive sign. See "Notes on Nomenclature" below for reasons for the differential usage of $φ_{\rm T}$ and $ϕ_{\rm T} = – φ_{\rm T}$.
Notes on Nomenclature:
- In this tutorial, as is common in other literature, the phase enters the equations with a negative sign when describing harmonic oscillation, Fourier series, and Fourier integrals, whereas in the context of modulation methods, the phase is always given a plus sign.
- To distinguish these two variants, we use $\phi_{\rm T}$ and $\varphi_{\rm T} = - \phi_{\rm T}$. Both symbols denote the lowercase Greek "phi", with the notation $\phi$ used predominantly in Anglo-American contexts, and $\varphi$ in German.
- The phase values $\varphi_{\rm T} = 90^\circ$ and $\phi_{\rm T} = -90^\circ$ are thus equivalent and both represent the sine function:
- $$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi_{\rm T}) = \cos(2 \pi f_0 t + \phi_{\rm T}) = \sin(2 \pi f_0 t ).$$
Further hints:
- This exercise belongs to the chapter General Model of Modulation.
- Particular reference is made to the page Describing the physical signal using the equivalent lowpass signal.
- Further information on this topic can be found in the following chapters of the book "Signal Representation":
- In our tutorial $\rm LNTwww$, the representation of the analytical signal $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{\rm TP}(t)$ angibt. Wir verweisen auf die entsprechenden interaktiven Applets
Fragebogen
Musterlösung
- die (normierte) Amplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 2}$ und die Periodendauer $T_0=2$ Millisekunden.
- Deshalb ist die Signalfrequenz $f_{\rm T} = 1/T_0\hspace{0.15cm}\underline{ = 500}$ Hz und die Kreisfrequenz beträgt $ω_{\rm T}= 2πf_{\rm T} \hspace{0.15cm}\underline{ = 3141.5}$ 1/s.
(2) Das analytische Signal lautet allgemein:
- $$z_+(t) = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}(\omega_{\rm T}\cdot \hspace{0.05cm}t + \phi_{\rm T})} = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_{\rm T}} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t }\hspace{0.05cm}.$$
- Gleichzeitig gilt der Zusammenhang:
- $$A_0 = z_+(t = 0) = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_{\rm T}} \hspace{0.05cm}.$$
- Die komplexe Amplitude $A_0$ kann aus der oberen Grafik abgelesen werden.
- $$A_0 = - \sqrt{2} - {\rm j} \cdot \sqrt{2} = A_{\rm 0} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 0.75 \pi} \hspace{0.05cm}.$$
- Ein Vergleich beider Gleichungen führt zum Ergebnis:
- $$ \phi_{\rm T} = - 0.75 \pi \hspace{0.15cm}\underline {= - 135^{\circ}} \hspace{0.05cm}.$$
- Dabei besteht folgender Zusammenhang mit der Laufzeit $τ$:
- $$\phi_{\rm T} = - 2 \pi \cdot f_{\rm T} \cdot \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \tau = \frac{-\phi_{\rm T}}{2 \pi \cdot f_{\rm T}} = \frac{0.75 \pi}{2 \pi \cdot 0.5\,{\rm kHz}} \hspace{0.15cm}\underline {= 0.75 \,{\rm ms}} \hspace{0.05cm}.$$
(3) Das analytische Signal legt in der Zeit $T_0$ genau eine Umdrehung zurück.
- Ausgehend von $A_0$ erreicht man somit nach $t_1 = T_0/8\hspace{0.15cm}\underline{ = 0.25}$ ms zum ersten Mal, dass das analytische Signal imaginär ist:
- $$z_+(t_1) = - 2 {\rm j}.$$
- Wegen der Beziehung $z(t) = {\rm Re}[z_+(t)]$ tritt zu diesem Zeitpunkt $t_1$ auch der erste Nulldurchgang des Signals $z(t)$ auf.
(4) Mit dem Ergebnis der Teilaufgabe (2) erhält man:
- $$ z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} = A_0 = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi_{\rm T}} = {\rm const.}$$
- Somit gilt für alle Zeiten $t$ und damit auch für $t = 1$ ms:
- $${\rm Re}[z_{\rm TP}(t)] = - \sqrt{2} \hspace{0.15cm}\underline {= -1.414} \hspace{0.05cm},$$
- $$ {\rm Im}[z_{\rm TP}(t)] = - \sqrt{2}\hspace{0.15cm}\underline {= -1.414} \hspace{0.05cm}.$$
(5) Richtig sind die Aussagen 1, 3 und 4:
- Die einzige Diracfunktion von $Z_+(f)$ liegt bei $f = f_{\rm T}$ und nicht bei $–f_{\rm T}$.
- Das analytische Signal einer harmonischen Schwingung ist immer komplex.
- Das äquivalente TP–Signal einer harmonischen Schwingung ist meistens komplex. Ausnahme:
- $$z(t) = ±A_{\rm T} · \cos(ω_{\rm T} · t) \ \Rightarrow \ z_{\rm TP}(t) = ±A_{\rm T}.$$