Modulation Methods/General Model of Modulation

1. Modulation Methods
2. General Description
3. General Model of Modulation

• Previous page
• Next page

• Previous page
• Next page

Joint description of amplitude and angle modulation

Joint description of amplitude and angle modulation

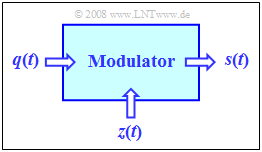
In the following two chapters  Amplitude Modulation  (AM) and  Angle Modulation  (WM – from German "Winkelmodulation", including PM as well as FM) we will always consider the set-up shown in the image on the right.  Here, the central block is the  Modulator.

The two input signals and the output signal have the following characteristics::

• The  source signal  $q(t)$  is the low frequency message signal and has the spectrum  $Q(f)$.  This signal is continuous in value and time and limited to the frequency range  $|f| ≤ B_{\rm NF}$ (NF from German "Niederfrequenz" i.e. low frequency).
  • The  carrier signal  $z(t)$  is a harmonic oscillation of the form

$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t - \varphi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$

• The  transmission signal  $s(t)$  is a higher frequency signal, whose spectral function  $S(f)$ is in the range around the carrier frequency $f_{\rm T}$ .

The modulator output signal  $s(t)$  depends on both input signals  $q(t)$  and  $z(t)$ .  The modulation methods considered below differ only by different combinations of  $q(t)$  and  $z(t)$.

$\text{Definition:}$  Each  Harmonic Oscillation  $z(t)$  can be described by

• the amplitude  $A_{\rm T}$,
• the frequency  $f_{\rm T}$  and
• the zero phase position  ${\it ϕ}_{\rm T}$ .

Though the above left equation with a minus sign and  $φ_{\rm T}$  is mostly used for the application of Fourier series and Fourier integrals, the right equation with  ${\it ϕ}_{\rm T} = \ – φ_{\rm T}$  and a plus sign is more common for the description of modulation processes.

A very simple (though unfortunately not always correct) modulator equation

$\text{Definition:}$  starting from the harmonic oscillation (here written with the angular frequency   $ω_{\rm T} = 2πf_{\rm T}$ )

$$z(t) = A_{\rm T} \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T})$$

we arrive at the  general modulator equation, by assuming the previously fixed oscillation parameters to be time-dependent:

$$s(t) = a(t) \cdot \cos \big[\omega(t) \cdot t + \phi(t)\big ]\hspace{0.05cm}.$$

$\text{!! Attention !!}$  This general modulator equation is very simple and striking and aids in understanding modulation methods.  Unfortunately, this equation is true for frequency modulation only in exceptional cases. This will be discussed further in the chapter  Signal characteristics in frequency modulation .

Special cases included in this equation are:

• In amplitude modulation  $\rm (AM)$,  the time-dependent amplitude  $a(t)$  changes according to the source signal $q(t)$, while the other two signal parameters stay constant:

$$\omega(t) = \omega_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm}\phi(t) = \phi_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm} a(t) = {\rm function \hspace{0.15cm}of}\hspace{0.15cm}q(t) .$$

• In frequency modulation  $\rm (FM)$,  only the instantaneous (circular) frequency $\omega(t)$  is determined by the source signal $q(t)$ :

$$a(t) = A_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm}\phi(t) = \phi_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm} \omega(t)= {\rm function \hspace{0.15cm}of}\hspace{0.15cm}q(t) .$$

• In phase modulation  $\rm (PM)$, the phase $\phi(t)$  varies according to the source signal $q(t)$:

$$a(t) = A_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm}\omega(t) = \omega_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm} \phi(t) = {\rm function \hspace{0.15cm}of}\hspace{0.15cm}q(t) .$$

In these basic methods, two of the three oscillation parameters are thus always kept constant.

• Additionally, there are also variants with more than one time dependency for amplitude, frequency, and phase, respectively.
• An example of this is  Single-Sideband Modulation, where both  $a(t)$  and  ${\it ϕ}(t)$  are affected by the source signal  $q(t)$ .

Modulated signals with a digital source signal

When describing   $\rm AM$,  $\rm FM$  and  $\rm PM$,  the source signal  $q(t)$  is usually assumed to be continuous in time and value.

• However, the above equations can also be applied to a rectangular source signal.
• In this case, $q(t)$  is continuous in time but discrete in value. Thus, it also describes methods for Linear Digital Modulation .

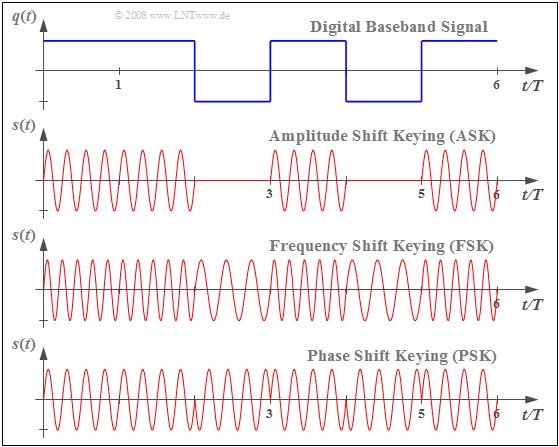
$\text{Example 1:}$  The graph shows a rectangular source signal  $q(t)$    ⇒   Baseband signal, at the top, and the modulated signals  $s(t)$ which result from important digital modulation methods drawn underneath.

Baseband signal together with   $\rm ASK$,  $\rm FSK$  and  $\rm PSK$

• In amplitude modulation, the digital variant of which is known as Amplitude Shift Keying  $\rm (ASK)$ , the message signal can be seen in the $s(t)$  envelope.

• In the Frequency Shift Keying  $\rm (FSK)$  signal waveform, the two possible signal values  $q(t) = +1$   and   $q(t) =-1$  are represented by two different frequencies, respectively.

• Phase Shift Keying  $\rm (PSK)$  results in phase jumps in the signal  $s(t)$ when the amplitude of the source signal  $q(t)$ jumps, by  $\pm π$  (or $\pm 180^\circ$) in each binary case.

Describing the physical signal using the analytic signal

The modulated signal   $s(t)$  is bandpass.  As already described in the book „Signal Representation”, a BP signal  $s(t)$  is often characterized by its associated  analytical signal  $s_+(t)$ . It is important to note:

• The analytical signal $s_+(t)$  is obtained from the real physical signal  $s(t)$, by adding to it, as an imaginary part, its Hilbert transform:

$$s_+(t) = s(t) + {\rm j} \cdot {\rm H}\{ s(t)\}\hspace{0.05cm}.$$

• The analytical signal  $s_+(t)$  is therefore always complex. The following simple relationship holds between the two time signals:

$$s(t) = {\rm Re} \big[s_+(t)\big] \hspace{0.05cm}.$$

• The spectrum  $S_+(f)$  of the analytic signal is obtained from the two-sided spectrum  $S(f)$ by doubling it for positive frequencies and setting it to zero for negative frequencies:

$$S_+(f) =\big[ 1 + {\rm sign}(f)\big] \cdot S(f) = \left\{ \begin{array}{c} 2 \cdot S(f) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} f>0 \hspace{0.05cm}, \\ f<0 \hspace{0.05cm}, \\ \end{array} \hspace{1.3cm} \text{with}\hspace{1.3cm} {\rm sign}(f) = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} f>0 \hspace{0.05cm}, \\ f<0 \hspace{0.05cm}. \\ \end{array}$$

Illustration of the analytical signal in the frequency domain

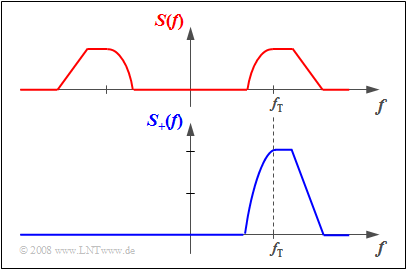
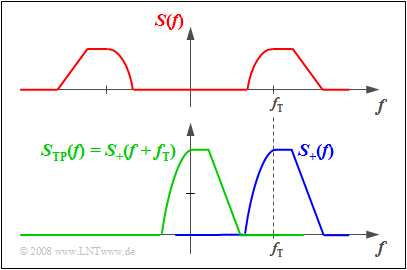
$\text{Example 2:}$  The above graph shows the spectrum  $S(f)$  of a real time signal  $s(t)$.  One can see:

• The axial symmetry of the spectral function  $S(f)$  with respect to the frequency  $f=0$:  

$${\rm Re}\big[S( - f)\big] = {\rm Re}\big[S(f)\big].$$

• If the spectrum of the actual time signal  $s(t)$  had an imaginary part, it would be point-symmetric about  $f=0$:

$${\rm Im}\big[S( - f)\big] = - {\rm Im}\big[S(f)\big].$$

The spectrum $S_+(f)$  of the corresponding analytical signal  $s_+(t)$  is shown below.  This is obtained from  $S(f)$  by

• Truncating the negative frequency components:   $S_+(f) \equiv 0$  for  $f<0$,
• Doubling the positive frequency components:   $S_+(f ) = 2 \cdot S(f )$  for  $f \ge 0$.

Except for an exceptional case that is not relevant in practice, the analytical signal  $s_+(t)$  is always complex.

We now apply these definitions to the modulated signal  $s(t)$ . In the special case that  $q(t) \equiv 0$ ,  $s(t)$ is a harmonic oscillation like the carrier signal  $z(t)$ .  It holds that:

$$s(t) = A_{\rm T} \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T}) \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_+(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}(\omega_{\rm T}\hspace{0.05cm} t \hspace{0.05cm} + \phi_{\rm T})}\hspace{0.05cm}.$$

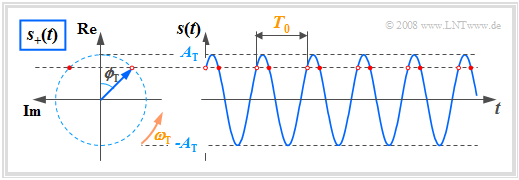
The second equation describes a rotating pointer with the following properties:

• The pointer length denotes the signal amplitude  $A_{\rm T}$.
• At time  $t = 0$ , the pointer lies in the complex plane with an angle of  $ϕ_{\rm T}$ .
• For  $t > 0$,  the pointer rotates with constant angular velocity  $ω_{\rm T}$  in a mathematically positive direction (counterclockwise).
• The pointer tip always lies on a circle with radius  $A_{\rm T}$  and requires exactly the period  $T_0$ for one rotation.

Illustration of the analytical signal in the time domain for  $ϕ_{\rm T} = -45^\circ$

To be display the relation  $s(t) = {\rm Re}[s_+(t)]$  horizontally, the complex plane is rotated by  $90^\circ$  to the left, contrary to the usual representation:

        The real part is plotted vertically and the imaginary part horizontally..
The individual modulation methods can now be represented as follows:

• In  amplitude modulation  the pointer length  $a(t) = |s_+(t)|$  changes and thus the envelope of  $s(t)$  changes according to the source signal  $q(t)$.
  The angular velocity  $ω(t)$  remains constant in this case.
• During  frequency modulation  the angular velocity  $ω(t)$  of the rotating pointer changes according to  $q(t)$,
  while the pointer length  $a(t) = A_{\rm T}$  stays unchanged.
• In  phase modulation,  the phase  $ϕ(t)$  is time-dependent.
  There are many similarities with frequency modulation, which also belongs to the class of angle modulation.

Describing the physical signal using the equivalent low pass signal

Some facts concerning modulation at the transmitting end and demodulation at the receiving end can be explained best by means of the equivalent lowpass signal  according to the definition given in the book "Signal Representation". 

The following statements hold for this signal  $s_{\rm TP}(t)$  (TP subscript from German "Tief-Pass" ⇒ lowpass) and its spectrum  $S_{\rm TP}(f)$ :

The equivalent lowpass signal in the frequency domain

• The spectrum  $S_{\rm TP}(f)$  of the equivalent lowpass signal is obtained from  $S_+(f)$  by shifting it to the left by  $f_{\rm T}$  and is thus in the frequency range around  $f =0$:

$$S_{\rm TP}(f) = S_+(f + f_{\rm T}) \hspace{0.05cm}.$$

• For the corresponding time function, according to the  Shifting Theorem, it holds that:

$$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{{-\rm j}\hspace{0.08cm} \omega_{\rm T} \hspace{0.03cm}t }\hspace{0.05cm}.$$

• The equivalent low-pass signal of an unmodulated harmonic oscillation is constant for all times –  the locus curve in this special case consists of a single point:

$$s(t) = A_{\rm T} \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T}) \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_+(t) = {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}(\omega_{\rm T}\hspace{0.05cm} t \hspace{0.05cm} + \phi_{\rm T})}\hspace{0.05cm},$$

$$ s_+(t) = {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}(\omega_{\rm T}\hspace{0.05cm} t \hspace{0.05cm} + \phi_{\rm T})}\hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.05cm} \phi_{\rm T}}\hspace{0.05cm}.$$

$\text{Important result:}$  Important result: for an amplitude or phase modulated signal with carrier frequency  $f_{\rm T}$  it holds that:

$$s(t) = a(t) \cdot \cos(\omega_{\rm T}\cdot t + \phi(t)) \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_{\rm TP}(t) = a(t) \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.05cm} \phi (t)}\hspace{0.05cm}.$$

The envelope  $a(t)$  and the phase response  $ϕ(t)$  of the (physical) bandpass signal are also preserved in the equivalent lowpass signal  $s_{\rm TP}(t)$ .

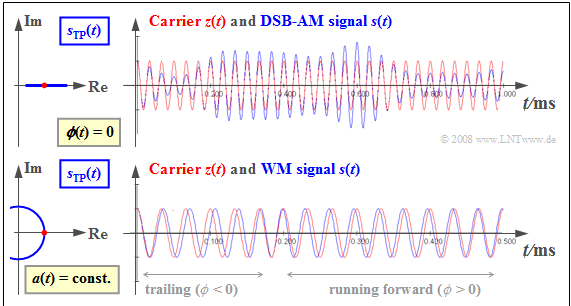
$\text{Example 3:}$  The graph shows the modulated signal  $s(t)$   ⇒   red signal waveform, compared to the carrier signal  $z(t)$   ⇒   blue signal waveform.
Shown on the left are the respective equivalent low-pass signals  $s_{\rm TP}(t)$   ⇒   green locus (CORRECTION NEEDED: GRAPH SHOWS LOCUS IN BLUE).

Transmitted signals for amplitude and angle modulation

  Amplitude modulation  is shown above, where the source signal  $q(t)$  can be seen in the envelope  $a(t)$ :

• Since the zero crossings of the carrier  $z(t)$  stay the same,  $ϕ(t) = 0$  and the equivalent lowpass signal  $s_{\rm TP}(t) = a(t)$  are real.

• This is derivation is done in the chapter  Description using the equivalent lowpass signal.

Below,   angle modulation  is illustrated.

• Here, the envelope  $a(t)$  is constant   ⇒   the equivalent lowpass signal  $s_{\rm TP}(t) = A_{\rm T} · e^{\rm j·ϕ(t)}$  describes a circular arc.
• The information about the message signal  $q(t)$  is found here in the location of the zero crossings  $s(t)$.
• More details about this can be found in the chapter Similarities between PM and FM

Hints:

• In the following, we also refer to the time-dependent course of  $s_{\rm TP}(t)$  in the complex plane as the "locus curve", whereas the "pointer diagram" describes the course of the analytical signal   $s_+(t)$ .
• The topic presented here is illustrated in the time domain with two interactive applets:

(1)  Physical & Analytic Signal ,

(2)  Physical Signal & Equivalent Lowpass Signal.

Exercises for the chapter

Exercise 1.4: Pointer diagram and locus curve

Exercise 1.4Z: Representation of Oscillations