Aufgaben:Exercise 1.3Z: Thermal Noise

• Return to book

Example signals for low-pass and band-pass noise

A fundamental disturbance and one that occurs in any communication system is  "thermal noise",  since any resistance  $R$  with an absolute temperature of  $θ$  (in "degrees Kelvin")  produces a noise signal  $n(t)$  with a  (one-sided)  noise power density

$${N_{\rm 0, \hspace{0.05cm}min}}= k_{\rm B} \cdot \theta \hspace{0.3cm}\left(k_{\rm B} = 1.38 \cdot 10^{-23} \hspace{0.05cm}{\rm Ws}/{\rm K}\right)$$

where $k_{\rm B}$  denotes the  "Boltzmann constant" (from German  "Konstante").

However,  this noise is limited to  $6\text{ THz}$  for physical reasons.  Furthermore,  it can be observed that this minimum value can only be achieved with exact impedance matching.

In the realization of a circuit unit - for example, an amplifier - the effective noise power density is usually significantly greater,  since several noise sources add up,  and mismatches also play a role.  This effect is captured by the noise factor  $F \ge 1$  .  It holds that:

$$N_0 = F \cdot {N_{\rm 0, \hspace{0.05cm}min}}= F \cdot k_{\rm B} \cdot \theta \hspace{0.05cm}.$$

With a bandwidth  $B$,  the effective noise power is characterized by:

$$N = N_0 \cdot B \hspace{0.1cm} \hspace{0.01cm}.$$

$$N = N_0 \cdot B\cdot R = \sigma_n^2 \hspace{0.01cm}.$$

• According to the first equation,  the result is the actual,  physical power in "watts"  $\rm (W)$.
• According to the second equation,  the result has the unit   „$\rm V^{ 2 }$”.
• This means that the power is here converted to the reference resistance  $R = 1\ Ω$  – as is often the case in Communications Engineering.
• This equation must also be used to calculate the rms value  ("standard deviation")  $σ_n$  of the noise signal  $n(t)$ .

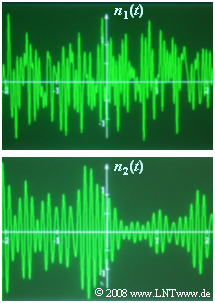
All equations apply regardless of whether the noise is low-pass or band-pass. The diagram shows two noise signals  $n_1(t)$  and  $n_2(t)$  of equal bandwidth.  Question   (4)  asks which of these signals will appear at the output of a low-pass and a band-pass, respectively.

The two-sided noise power density of band-limited low-pass noise  $n_{\rm TP}(t)$  is:

$$ {\it \Phi}_{n, {\hspace{0.05cm}\rm LP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{for}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < B,} \\ {\rm otherwise.} \\ \end{array}$$

In contrast,  for band-pass noise  $n_{\rm BP}(t)$  with center frequency  $f_{\rm M}$, it holds that:

$${\it \Phi}_{n, {\hspace{0.05cm}\rm BP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{for}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f - f_{\rm M}\hspace{0.05cm} \right| < B/2,} \\ {\rm otherwise.} \\ \end{array}.$$

For all subsequent numerical calculations it is assumed:

$$ F = 10, \hspace{0.2cm}\theta = 290\,{\rm K},\hspace{0.2cm}R = 50\,{\rm \Omega},\hspace{0.2cm}B = 30\,{\rm kHz},\hspace{0.2cm}f_{\rm M} = 0 \hspace{0.5cm}{\rm or}\hspace{0.5cm}f_{\rm M} =100\,{\rm kHz}\hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  Quality Criteria.
• Particular reference is made to the page  Some remarks on the AWGN channel model.
• By specifying the powers in  $\rm W$atts , they are independent of the reference resistance  $R$,  while power with the unit  $\rm V^2$  can only be evaluated directly for  $R = 1\ \Omega$.

Questions

1

Calculate the noise power density  $N_0$  with a noise factor of  $F = 10$  and  $θ = 290^\circ$  Kelvin.

$N_0 \ = \ $ $\ \cdot 10^{ -20 }\ \text{W/Hz}$

2

What is the maximum noise power  (without bandwidth limits)?

$N_{\rm max} \ = \ $ $\ \cdot 10^{ -6 }\ \text{W/Hz}$

3

What is the noise power  $N$  with bandwidth  $B = 30\text{ kHz}$?  What is the rms value $σ_n$?

$N \ = \ $ $\ \cdot 10^{ -16 }\ \text{W/Hz}$

$σ_n \ = \ $ $\ \cdot 10^{ -6 }\ \text{V}$

4

Which of the signals –  $n_1(t)$  or  $n_2(t)$  – shows low-pass noise and which shows band-pass noise?

	The noise signal  $n_1(t)$  is characteristically low-pass.
	The noise signal  $n_1(t)$  is characteristically band-pass.

5

What is the value of the noise power density of the low-pass  $\rm (LP)$  noise at frequency  $f = 20\text{ kHz}$?  Let  $B = 30\text{ kHz}$.

${\it Φ}_{n, \hspace{0.05cm}\rm LP}(f = 20 \ \rm kHz) \ = \ $ $\ \cdot 10^{ -12 }\ \text{W/Hz}$

6

What is the value of the noise power density of the band-pass  $\rm (BP)$  noise at  $f = 120\text{ kHz}$?  Let  $f_{\rm M} = 100\text{ kHz}$  and  $B = 30\text{ kHz}$.

${\it Φ}_{n, \hspace{0.05cm}\rm BP}(f = 120 \ \rm kHz) \ = \ $ $\ \cdot 10^{ -12 }\ \text{W/Hz}$

Solution

Solution

(1)  Using the Boltzmann constant  $k_{\rm B}$  it holds that:

$$N_0 = F \cdot k_{\rm B} \cdot \theta = 10 \cdot 1.38\hspace{0.05cm}\cdot 10^{-23} \hspace{0.05cm}\frac{\rm Ws}{\rm K}\cdot 290\,{\rm K} \hspace{0.15cm}\underline {\approx 4\hspace{0.05cm}\cdot 10^{-20} \hspace{0.05cm}{\rm W}/{\rm Hz}}\hspace{0.05cm}.$$

(2)  The specified noise power density  $N_0$  is physically limited to  $6$  THz.  Thus the maximum noise power is:

$$N_{\rm max} = 4\hspace{0.05cm}\cdot 10^{-20} \hspace{0.08cm}\frac{\rm W}{\rm Hz}\cdot 6 \cdot10^{12} \hspace{0.08cm}{\rm Hz}\hspace{0.15cm}\underline {= 0.24\hspace{0.08cm}\cdot 10^{-6}\;{\rm W}}\hspace{0.05cm}.$$

(3)  Now the resulting noise power is:

$$N = N_0 \cdot B = 4\hspace{0.08cm}\cdot 10^{-20} \hspace{0.08cm}\frac{\rm W}{\rm Hz}\cdot 3 \cdot10^{4} \hspace{0.08cm}{\rm Hz}\hspace{0.15cm}\underline {= 12\hspace{0.05cm}\cdot 10^{-16}\;{\rm W}}\hspace{0.05cm}.$$

• Converting to the reference resistance  $R = 1 \ Ω$:

$$N = N_0 \cdot B \cdot R = 12\hspace{0.05cm}\cdot 10^{-16}\;{\rm W}\hspace{0.05cm} \cdot 50 \; {\rm \Omega}= 6\hspace{0.05cm}\cdot 10^{-14}\;{\rm V^2}\hspace{0.05cm}.$$

Power density spectra with band-limited noise

• The noise rms value $σ_n$  is the square root of this:

$$\sigma_n= \sqrt{6\hspace{0.05cm}\cdot 10^{-14}\;{\rm V^2}} \hspace{0.15cm}\underline {= 0.245 \hspace{0.05cm}\cdot 10^{-6}\;{\rm V}}\hspace{0.05cm}.$$

(4)  Answer 1  is correct:

• In the random signal  $n_2(t)$ one can recognize certain regularities similar to a harmonic oscillation   ⇒   it is bandpass noise.
• In contrast, the signal  $n_1(t)$  is low-pass noise.

(5)  The noise power density of the random signal  $n_1(t)$  is constant in the frequency range  $|f| < 30$  kHz:

$${\it \Phi}_{n,\hspace{0.05cm}{ \rm LP} }(f) \hspace{-0.05cm}=\hspace{-0.05cm} \frac{N_0}{2} \hspace{0.15cm}\underline {=2\hspace{0.05cm}\hspace{-0.05cm}\cdot \hspace{-0.05cm} 10^{-12} \hspace{0.05cm}{\rm W}/{\rm Hz}}\hspace{0.05cm}.$$

• Thus,  this value is also valid for the frequency  $f = 20$  kHz.

(6)  As can be seen from the diagram,   ${\it Φ}_{n, \hspace{0.05cm}\rm BP}(f)$  is non-zero only in the range between  $85$  kHz and  $115$  kHz,  when the bandwidth is  $B = 30$  kHz.

• Thus,  at the frequency   $f = 120$  kHz, the noise power density is zero:

$${\it Φ}_{n, \hspace{0.05cm}\rm BP}(f = 120 \ \rm kHz)\hspace{0.15cm}\underline{=0}.$$