Difference between revisions of "Aufgaben:Exercise 4.7: Copper Twin Wire 0.5 mm"
From LNTwww
| Line 121: | Line 121: | ||
*The partial impulse response $h_1(t ) \star h_2(t )$ takes into account the influence of $\alpha_1$, $\alpha_2$ and $\beta_2$ and thus all terms leading to distortions. | *The partial impulse response $h_1(t ) \star h_2(t )$ takes into account the influence of $\alpha_1$, $\alpha_2$ and $\beta_2$ and thus all terms leading to distortions. | ||
*In contrast, $\alpha_0$ leads only to a frequency-independent attenuation and $\beta_1$ only to a constant running time for all frequencies. | *In contrast, $\alpha_0$ leads only to a frequency-independent attenuation and $\beta_1$ only to a constant running time for all frequencies. | ||
| − | *Solution 2 does not apply: First (for small $t$–values) $h_1(t ) \star h_2(t )$ is smaller than $h_2(t )$. Then, for large $t$–values, the blue curve lies above the red one. | + | *Solution 2 does not apply: First (for small $t$–values) $h_1(t ) \star h_2(t )$ is smaller than $h_2(t )$. |
| + | *Then, for large $t$–values, the blue curve lies above the red one. | ||
*This means: $\alpha_1$ and thus also $h_1(t )$ actually cause additional distortions, even when they are not very significant. | *This means: $\alpha_1$ and thus also $h_1(t )$ actually cause additional distortions, even when they are not very significant. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:52, 24 November 2021
The time response of a copper twin wire with diameter $d = 0.5 \ \rm mm$ is to be analyzed.
- The frequency response with the line length $l = 1.5 \ \rm km$ and the bit rate $R = 10 \ \rm Mbit/s$:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm a}_0 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.01cm}\tau_{\rm P}} \cdot {\rm e}^{-{\rm a}_1 \hspace{0.05cm}\cdot \hspace{0.02cm}2f/R}\cdot {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}} \hspace{0.05cm}.$$
- The following quantities are used, which can be derived from the attenuation and phase function per unit length:
- $${\rm a}_0 = \alpha_0 \cdot l\hspace{0.05cm},\hspace{0.2cm}{\rm with} \hspace{0.15cm}\alpha_0 = 0.5066\,\, \frac{\rm Np}{\rm km}\hspace{0.05cm},$$
- $$ \tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi} \hspace{0.05cm},\hspace{0.2cm}{\rm with} \hspace{0.15cm}\beta_1 = 30.6\,\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm},$$
- $$ {\rm a}_1 = \alpha_1 \cdot l \cdot {{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm with} \hspace{0.15cm} \alpha_1 = 0.136\,\, \frac{\rm Np}{\rm km \cdot MHz}\hspace{0.05cm},$$
- $$ {\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm with} \hspace{0.15cm} \alpha_2 = 1.1467\,\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},$$
- $$ {b}_2 = \beta_2 \cdot l \cdot \sqrt{{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm with} \hspace{0.15cm} \beta_2 = 1.1467\,\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm}.$$
- The impulse response can thus be expressed in the form
- $$h_{\rm K}(t ) = K \cdot \big [ \delta(t - \tau_{\rm P})\star h_{1}(t) \star h_{2}(t) \big ]$$
where
- the partial impulse response $h_1(t)$ is due to the third term in the frequency domain equation, and
- $h_2(t)$ indicates the joint time-domain representation of the last two terms.
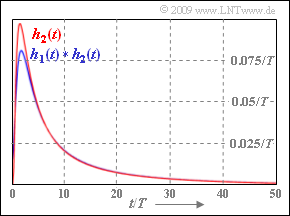
The graph shows as red curve the part $h_2(t)$ of the impulse response and the convolution product $h_1(t) \star h_2(t)$ ⇒ blue curve).
Here $h_2(t)$ is equal to the coaxial cable impulse response with the characteristic cable attenuation ${\rm a}_\star = {\rm a}_2$.
Notes:
- The exercise belongs to the chapter Properties of Balanced Copper Pairs.
- The parameters $\alpha_0$, $\alpha_1$ and $\alpha_2$ were converted from the $k$–parameters as shown in Exercise 4.6.
- The phase function parameter $\beta_2$ was set here numerically equal to the attenuation function parameter $\alpha_2$.
- Therefore, the attenuation component ${\rm a}_2$ and the phase component ${b}_2$ differ only in units.
- On the page Discussion of the approximate solution found, it is explained why this measure is necessary.
- You can use the (German language) interactive SWF applet "Zeitverhalten von Kupferkabeln" ⇒ "Time behavior of copper cables" to check your results.
Questions
Solution
(1) With ${\rm a}_0 = \alpha_0 \cdot l \approx 0.76 \ \rm Np$, for the constant $K$, which indicates the influence of the coefficient $ \alpha_0$ on the impulse response, we obtain:
- $$K = {\rm e}^{-{\rm a}_0 }= {\rm e}^{-0.76} \hspace{0.15cm}\underline{= 0.468} \hspace{0.05cm}.$$
(2) For the phase delay, using the given equation:
- $$\tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi}= \frac{30.6 \cdot 1.5}{2 \pi}\, {\rm µ s}\approx 7.31\, {\rm µ s}\hspace{0.05cm},$$
and related to the symbol duration $T = 0.1 \ µ \rm s$:
- $${\tau_{\rm P}}/{T} \hspace{0.15cm}\underline{ \approx 73}\hspace{0.05cm}.$$
(3) The impulse response of a coaxial cable is approximately equal to $h_2(t)$, if the cable has the following characteristic cable attenuation:
- $${\rm a}_\star ={\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}} = 1.1467\,\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot 1.5\,{\rm km} \cdot \sqrt{\frac{10\,{\rm MHz}}{2}} = 2.93\,{\rm Np} = 2.93\,{\rm Np} \cdot8.686\,\frac {\rm dB}{\rm Np} \hspace{0.15cm}\underline{ =25.5\,{\rm dB}}\hspace{0.05cm}.$$
(4) Statements 1 and 2 are correct:
- The Fourier transform $H_1(f) = {\rm e}^{-A \hspace{0.05cm} \cdot \hspace{0.05cm} |f|}$ with $A = 2 \hspace{0.05cm}\cdot \hspace{0.05cm} {a}_1/R$ is real and even, so $h_1(t)$ is also real and even.
- Due to the low–pass characteristic of $H_1(f)$, the maximum is at $t = 0$.
- The last statement, on the other hand, is incorrect: The integral over $h_1(t)$ in the entire time domain $ \pm \infty$ is equal to $H_1(f=0) = 1$.
(5) Only solution 1 is correct:
- The partial impulse response $h_1(t ) \star h_2(t )$ takes into account the influence of $\alpha_1$, $\alpha_2$ and $\beta_2$ and thus all terms leading to distortions.
- In contrast, $\alpha_0$ leads only to a frequency-independent attenuation and $\beta_1$ only to a constant running time for all frequencies.
- Solution 2 does not apply: First (for small $t$–values) $h_1(t ) \star h_2(t )$ is smaller than $h_2(t )$.
- Then, for large $t$–values, the blue curve lies above the red one.
- This means: $\alpha_1$ and thus also $h_1(t )$ actually cause additional distortions, even when they are not very significant.