Modulation Methods/Single-Sideband Modulation

1. Modulation Methods
2. Amplitude Modulation and Demodulation
3. Single-Sideband Modulation

• Previous page
• Next page

• Previous page
• Next page

Description in the frequency domain

Double sideband amplitude modulation $\rm (DSB–AM)$  – both with and without a carrier – has the following characteristics:

• the modulated signal  $s(t)$  requires twice the bandwidth of the source signal  $q(t)$.
• The complete information about  $q(t)$  is in both the upper sideband   $\rm (USB)$  as well as in the lower sideband  $\rm (LSB)$.

So-called  single-sideband amplitude modulation  $\rm (SSB–AM)$  takes advantage of this property by transmitting only one of these sidebands, either the upper sideband (USB) or the lower sideband (LSB). This reduces the required bandwidth by half compared to DSB-AM.

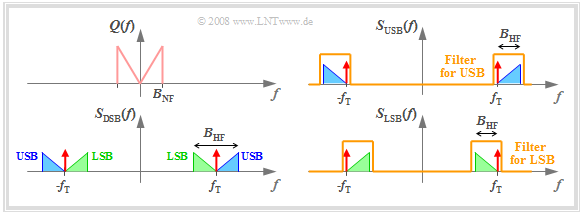
The graph illustrates single-sideband amplitude modulation in the frequency domain and simultaneously presents a realization of a SSB Modulator. 

Spectra for double sideband and single-sideband modulation

In this representation, one can see:

• The SSB spectrum results from the DSB spectrum by filtering with a bandpass which displays asymmetrical behaviour with respect to the carrier frequency  $f_{\rm T}$ .
• For USB modulation, the lower cutoff frequency is chosen at  $f_{\rm U} = f_{\rm T} - f_ε$  and the upper cutoff frequency at  $f_{\rm O} ≥ f_{\rm T} + B_{\rm NF}$ .  Here,  $f_ε$  denotes an arbitrarily small positive frequency.
• Thus, the USB spectrum only contains the upper sideband and the carrier (though not necessarily the latter).
• To generate a USB modulation, the upper and lower cutoff frequencies of the bandpass must be set as follows:

$$f_{\rm U} ≤ f_{\rm T} \ - \ B_{\rm NF}, \hspace{0.5cm}f_{\rm O} = f_{\rm T} + f_ε.$$

$\text{Example 1:}$  For  $f_{\rm T} = 100 \ \rm kHz$  and  $B_{\rm NF} = 3 \ \rm kHz$  we obtain an USB signal with carrier from the DSB signal if the filter cuts out all frequencies below  $99.999\text{...} \ \rm kHz$ .

• If the lower cutoff frequency  $f_{\rm U}$  is larger than  $f_{\rm T}$ by an (arbitrarily) small "epsilon", we get an "USB-AM without carrier".
• A "LSB with/without carrier" can be realised accordingly, with  $f_{\rm O} =100 \ \rm kHz$  and  $f_{\rm O} = 99.999\text{...} \ \rm kHz$, respectively.

$\text{Example 2:}$  To save bandwidth, single-sideband technology was already used in the 1960s for the analog transmission of telephone calls.

• In accordance with a hierarchical structure, three telephone channels – each band-limited to the range from  $300\ \rm Hz$  to  $3.4 \ \rm kHz$  – were initially combined to form a preliminary grouping with a bandwidth of  $12 \ \rm kHz$ .
• In order to be able to accommodate three channels in  $12 \ \rm kHz$  with a certain safety margin, only one sideband (the lower or the upper) of each telephone channel was considered.
• Using further combinations, the long distance traffic system V10800 with up to 10800 voice channels and a total bandwidth of  $60 \ \rm MHz$  was thus realized.

$\text{Conclusion:}$ 

• The great advantage of a SSB-AM is that it has a half bandwidth compared to DSB-AM.
• The trade-off with disadvantages required for this advantage is explained in the next pages.

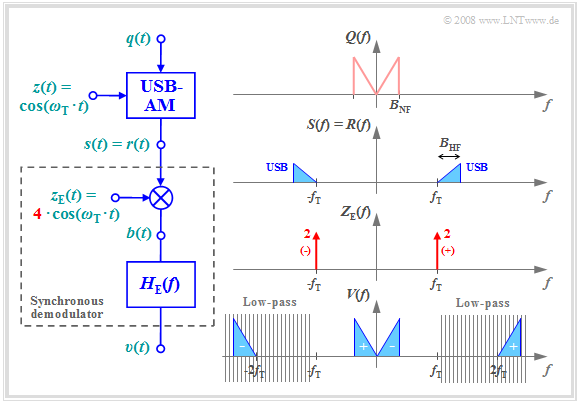
Synchronous demodulation of a SSB signal

Let us now consider a SSB modulated signl and a  synchronous demodulator at the receiver.

• Perfect frequency and phase synchronization will be assumed.
• Without affecting generality, in the rest of this section we will always let  ${ ϕ}_{\rm T} = 0$  ⇒   cosine carrier.

Synchrondemodulation eines ESB–Signals

Ein Vergleich mit den Eigenschaften des Synchrondemodulators bei ZSB–AM im vorletzten Kapitel zeigt folgende Gemeinsamkeiten und Unterschiede:

• Das Spektrum  $V(f)$  des Sinkensignals ergibt sich in beiden Fällen aus der Faltung der Spektren  $R(f)$  und  $Z_{\rm E}(f)$, wobei Letzteres sich aus zwei Diracfunktionen bei  $±f_{\rm T}$  zusammensetzt.

• Bei ZSB–AM überlagern sich für jede Frequenz die Faltungsprodukte mit der rechten und der linken Diracfunktion. In der entsprechenden ZSB–Grafik sind diese Anteile mit „+” bzw. „–” markiert.

• Dagegen liefert bei OSB–Modulation nur die Faltung mit der Diraclinie bei  $ -f_{\rm T}$  den  $V(f)$–Anteil bei positiven Frequenzen und bei USB–Modulation die Faltung mit der Diracfunktion  $δ(f - f_{\rm T})$.

• Bei ZSB–AM wird  $v(t) = q(t)$  mit dem empfangsseitigen Trägersignal  $z_{\rm E}(t) = 2 · \cos(ω_{\rm T} · t)$  erreicht.  Dagegen muss bei ESB–AM die Trägeramplitude auf  $A_{\rm T} = 4$   erhöht werden.

$\text{Fazit:}$  Besteht ein Frequenzversatz zwischen den Trägersignalen  $z(t)$  und  $z_{\rm E}(t)$, so kommt es stets zu starken nichtlinearen Verzerrungen, also unabhängig davon, ob ZSB–AM oder ESB–AM vorliegt.  Bei der  Realisierung eines Synchrondemodulators  ist deshalb eine  perfekte Frequenzsynchronisation  unerlässlich.

Einfluss eines Phasenversatzes bei ESB-AM

Betrachten wir nun den Einfluss eines Phasenversatzes  $Δ{\mathbf ϕ}_{\rm T}$  zwischen sende– und empfangsseitigem Trägersignal, und zwar am Beispiel des Quellensignals

$$q(t) = A_1 \cdot \cos(\omega_1 \cdot t ) + A_2 \cdot \cos(\omega_2 \cdot t)\hspace{0.05cm}.$$

• Bei ZSB–AM führt ein solcher Phasenversatz lediglich zu einer frequenzunabhängigen Dämpfung, aber nicht zu Verzerrungen:

$$v(t) = \cos (\Delta \phi_{\rm T}) \cdot q(t) = \cos (\Delta \phi_{\rm T}) \cdot A_1 \cdot \cos(\omega_1 \cdot t ) + \cos (\Delta \phi_{\rm T}) \cdot A_2 \cdot \cos(\omega_2 \cdot t ) \hspace{0.05cm}.$$

• Dagegen erhält man bei der OSB–AM:

$$v(t) = A_1 \cdot \cos(\omega_1 \cdot t - \Delta \phi_{\rm T}) + A_2 \cdot \cos(\omega_2 \cdot t - \Delta \phi_{\rm T})= A_1 \cdot \cos(\omega_1 \cdot (t - \tau_1)) + A_2 \cdot \cos(\omega_2 \cdot (t - \tau_2))\hspace{0.05cm}.$$

$\text{Man erkennt aus dieser Gleichung:}$

• Die beiden Laufzeiten  $τ_1 = Δ{\mathbf ϕ}_{\rm T}/ω_1$  und  $τ_2 = Δ{\mathbf ϕ}_{\rm T}/ω_2$  sind unterschiedlich.
• Das bedeutet, dass ein Phasenversatz bei ESB–AM (OSB–AM oder USB–AM) zu  Phasenverzerrungen  (also zu linearen Verzerrungen) führt.
• Ein positiver Wert von  $Δ{\mathbf ϕ}_{\rm T}$  bewirkt
  • bei OSB positive Werte von  $τ_1$  und  $τ_2$  (also gegenüber dem Cosinus nachlaufende Signale)  und
  • bei USB negative  $τ_1$–  bzw.  $τ_2$–Werte  (vorlaufende Signale).

Die Auswirkungen von Phasenverzerrungen auf ein aus zwei Cosinusschwingungen zusammengesetztes Nachrichtensignal können Sie sich mit dem interaktiven Applet  Lineare Verzerrungen periodischer Signale  verdeutlichen.

Seitenband–zu–Träger–Verhältnis

Spektren bei ZSB- und ESB-AM

Ein wichtiger Parameter der ZSB–AM ist der  Modulationsgrad  $m = q_{\rm max}/A_{\rm T}$.

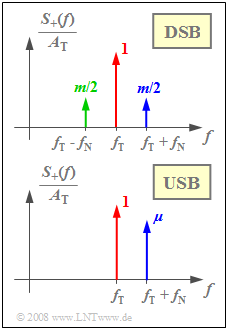
Im Sonderfall einer harmonischen Schwingung gilt  $m = A_{\rm N}/A_{\rm T}$  und man erhält das Spektrum  $S_+(f)$  des analytischen Signals entsprechend der oberen Grafik.  Beachten Sie bitte die Normierung auf  $A_{\rm T}$.

Bei der ESB–AM ist die Anwendung des Parameters  $m$  zwar prinzipiell möglich, aber nicht zweckmäßig.  Beispielsweise gilt für die Zeitbereichsdarstellung der OSB–AM mit dem Spektrum  $S_+(f)$  entsprechend der unteren Grafik:

$$s_+(t) = A_{\rm T} \cdot {\rm e}^{{\rm j}\hspace{0.03cm}\cdot \hspace{0.05cm} \omega_{\rm T} \hspace{0.03cm}\cdot \hspace{0.05cm}t } + {A_{\rm N}}/{2} \cdot {\rm e}^{{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} (\omega_{\rm T} + \omega_{\rm N}) \hspace{0.05cm}\cdot \hspace{0.05cm}t }\hspace{0.05cm}.$$

Hierfür kann in gleicher Weise

$$s_+(t) = A_{\rm T} \cdot \left({\rm e}^{{\rm j}\hspace{0.03cm}\cdot \hspace{0.05cm} \omega_{\rm T} \hspace{0.03cm}\cdot \hspace{0.05cm}t } + \mu \cdot {\rm e}^{{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} (\omega_{\rm T} + \omega_{\rm N}) \hspace{0.03cm}\cdot \hspace{0.05cm}t }\right)$$

geschrieben werden, wobei nun das  Seitenband–zu–Träger–Verhältnis  verwendet ist:

$$\mu = \frac{A_{\rm N}}{2 \cdot A_{\rm T}} \hspace{0.05cm}.$$

Ist das Quellensignal keine harmonische Schwingung, so ist die Angabe dieser Größe schwierig.

• Hier kann man folgende Näherung benutzen:

$$\mu \approx \frac{q_{\rm max}}{2 \cdot A_{\rm T}} \hspace{0.3cm}{\rm mit}\hspace{0.3cm} q_{\rm max} = \max_{t} \hspace{0.05cm} |q(t)| \hspace{0.05cm}.$$

• Somit ist  $\mu \approx m/2.$  Ein Vergleich zwischen ZSB–AM und ESB-AM sollte jedoch stets für den gleichen Zahlenwert von  $m$  bzw.  $\mu$  erfolgen.

Signalverläufe bei ZSB_AM und OSB-AM

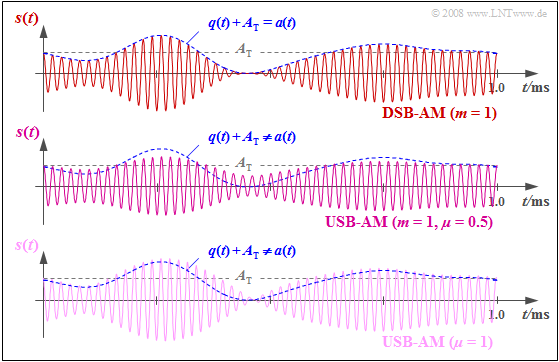
$\text{Beispiel 3:}$  Die obere Grafik zeigt das ZSB–AM–Signal für den Modulationsgrad  $m = q_{\rm max}/A_{\rm T} = 1$   ⇒   Grenzfall für die Anwendung der Hüllkurvendemodulation bei ZSB-AM:  
⇒   Das Nachrichtensignal  $q(t)$  ist dann in der Hüllkurve  $a(t)$  gerade noch verzerrungsfrei enthalten.

Für das OSB–Signal in der mittleren Grafik zeigt wurde ebenfalls  $A_{\rm T} = q_{\rm max}$  gewählt, was nach obigen Definitionen den Zahlenwerten  $m = 1$  bzw.  $\mu = 0.5$  entspricht.
⇒   Da der USB-Beitrag fehlt, unterscheidet sich hier die Hüllkurve  $a(t)$  deutlich von  $q(t) + A_{\rm T}.$

Dagegen wurde für den unteren Signalverlauf  $q_{\rm max} = 2 · A_{\rm T}$  gewählt.
⇒   Das Seitenband–zu–Träger–Verhältnis hat hier den Zahlenwert  $\mu =1$.
Diese Grafik macht Folgendes deutlich:

• Es sind mehr Ähnlichkeiten zwischen dem oberen und dem unteren Signal festzustellen als zwischen den ersten beiden   ⇒   der Vergleich zwischen einer ZSB–AM und einer ESB–AM sollte möglichst bei gleichem Zahlenwert für  $m$  bzw.  $\mu$  erfolgen.
• Die Hüllkurvendemodulation führt bei einer Einseitenband–Amplitudenmodulation grundsätzlich – das heißt für jeden Zahlenwert des Seitenband–zu–Träger–Verhältnisses  $\mu$ – zu gravierenden Verzerrungen.  Diese sind von nichtlinearer Art und somit irreversibel.

Zusammenfassende Bewertung der ESB–AM

Der entscheidende Vorteil der ESB–AM gegenüber der ZSB–AM ist der um den Faktor  $2$  geringere Bandbreitenbedarf.  Für die halbe Bandbreite der ESB–AM müssen aber auch Nachteile in Kauf genommen werden, die in den Aufgaben zu diesem Abschnitt untersucht werden sollen:

• Die Information über das Quellensignal  $q(t)$  steckt nun im Gegensatz zur ZSB–AM nicht mehr ausschließlich in der Amplitude, sondern gleichermaßen auch in der Phase
  (siehe Aufgabe 2.11).
• Die Anwendung der Hüllkurvendemodulation bei OSB– oder USB–AM führt deshalb stets zu starken nichtlinearen Verzerrungen  (siehe Aufgabe 2.11Z).
• Synchrondemodulation eines ESB–AM–Signals führt zu Phasenverzerrungen, wenn zwischen den Trägersignalen bei Sender und Empfänger ein Phasenversatz besteht.

Ebenso wie bei einer ZSB–AM mit Synchrondemodulation gelten auch hier folgende Aussagen:

• Dämpfungsverzerrungen des Kanals führen ebenfalls nur zu  (linearen)  Dämpfungsverzerrungen bezüglich des Sinkensignals.  Es entstehen keine nichtlinearen Verzerrungen  (siehe  Aufgabe A2.10).
• Die ESB–AM ohne Träger zeigt genau gleiches Rauschverhalten wie die ZSB–AM ohne Träger.  Der Vorteil der kleineren HF–Bandbreite wird durch die notwendige Pegelanpassung aufgehoben.
• Eine ESB–AM mit Seitenband–zu–Träger–Verhältnis  $\mu$  zeigt ähnliches Rauschverhalten wie eine ZSB–AM mit Modulationsgrad  $m = \sqrt{2} · \mu$  (siehe  Aufgabe 2.10Z).
• Allerdings ist zu beachten, dass die ESB–AM mit Träger aufgrund der nichtlinearen Verzerrungen bei Hüllkurvendemodulation wenig sinnvoll ist.

Aufgaben zum Kapitel

Aufgabe 2.10: ESB-AM mit Kanalverzerrungen

Aufgabe 2.10Z: Rauschen bei ZSB-AM und ESB-AM

Aufgabe 2.11: Hüllkurvendemodulation eines ESB-Signals

Aufgabe 2.11Z: Nochmals ESB-AM und Hüllkurvendemodulator