Difference between revisions of "Aufgaben:Exercise 5.10: DMT Process for DSL"
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Further_OFDM_Applications |
}} | }} | ||
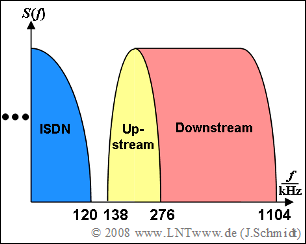
| − | [[File:P_ID1669__Mod_A_5_10.png|right|frame| | + | [[File:P_ID1669__Mod_A_5_10.png|right|frame|Bandwidth organization for $\rm DSL$]] |
| − | + | In this exercise we consider a $\rm DSL$ System ("Digital Subscriber Line"), where for modulation | |
| − | *[[ | + | *[[Examples_of_Communication_Systems/xDSL_als_Übertragungstechnik#Grundlagen_von_DMT_.E2.80.93_Discrete_Multitone_Transmission|$\rm DMT$]] ("Discrete Multitone Transmission") |
| − | * | + | * with $N = 512$ grid points |
| − | |||
| − | |||
| − | |||
| − | |||
| + | is used. In this context, the carriers are also referred to as "bins". | ||
| − | + | For DSL is specified: | |
| − | * | + | * The carrier spacing is $f_0 = 4.3125\ \rm kHz$. |
| − | * | + | * For the spectrum holds: $S(f = 0) = 0$. |
| + | * The so-called "Nyquist tone" is also set to zero: $S(256 · f_0) = 0$. | ||
| − | + | The diagram shows the bandwidth organization of the considered system for positive frequencies: | |
| − | * | + | *A transmission frame of $\rm DMT$ is composed of the core symbol duration $T$ and the duration $T_{\rm G}$ of the cyclic prefix, as in OFDM. This consists of $N_{\rm G} = 32$ samples. |
| − | + | *For synchronization between transmitter and receiver, a synchronization frame is sent after every $68$ frames, which does not contain any user data. | |
| − | |||
| − | * | ||
| − | === | + | |
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Modulation_Methods/Weitere_OFDM–Anwendungen|Further OFDM Applications]]. | ||
| + | *Reference is made in particular to the sections [[Modulation_Methods/Further_OFDM_Applications#A_brief_description_of_DSL_-_Digital_Subscriber_Line|A brief description of DSL]] and [[Modulation_Methods/Further_OFDM_Applications#Differences_between_DMT_and_the_described_OFDM|Differences between DMT and the described OFDM]]. | ||
| + | * For more information on the topic, refer to the second chapter: $\rm DSL$ – "Digital Subscriber Line" of the LNTwww book [[Examples_of_Communication_Systems]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements is correct? |
| − | |type=" | + | |type="()"} |
| − | - | + | - DSL is a bandpass system. |
| − | + DSL | + | + DSL is operated in the baseband. |
| − | { | + | {Which of the following statements is true about the DMT time signal? |
| − | |type=" | + | |type="()"} |
| − | + | + | + The time signal is purely real. |
| − | - | + | - The time signal is purely imaginary. |
| − | - | + | - The time signal is complex. |
| − | { | + | {How many bins are available for the upstream and the downstream? |
|type="{}"} | |type="{}"} | ||
| − | $N_{Up}$ | + | $N_{\rm Up} \ = \ $ { 32 } |
| − | $N_{Down}$ | + | $N_{\rm Down} \ = \ $ { 192 } |
| − | { | + | {Specify the duration $T$ of the core symbol. |
|type="{}"} | |type="{}"} | ||
| − | $T$ | + | $T \ = \ $ { 232 3% } $\ \rm µ s$ |
| − | { | + | {What is the duration $T_{\rm G}$ of the guard interval? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $T_{\rm G} \ = \ $ { 14 3% } $\ \rm µ s$ |
| − | { | + | {What is the value of the frame duration $T_{\rm R}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $T_{\rm R} \ = \ $ { 246 3% } $\ \rm µ s$ |
| − | { | + | {Specify the useful bit rate of the system shown for the downstream when $\rm BPSK$ is used for all carriers. |
|type="{}"} | |type="{}"} | ||
| − | $R_{B,Down}$ | + | $R_\text {B, Down} \ = \ $ { 768 3% } $\ \rm kbit/s$ |
| − | { | + | {Let the $198$th grid point of the (finite) DMT spectrum be $1 + 3 · {\rm j}$. Determine the (complex) value of the $314$th grid point. |
|type="{}"} | |type="{}"} | ||
| − | $\text{Re | + | $\text{Re}\big[S(314 · f_0)\big] \ = \ $ { 1 3% } |
| − | $\text{Im | + | $\text{Im}\big[S(314 · f_0)\big] \ = \ $ { -3.09--2.91 } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''(1)''' <u>Solution 2</u> is correct: |
| + | *DSL is a baseband system. | ||
| + | *In contrast, mobile radio systems are bandpass systems which are operated in correspondingly high frequency ranges. | ||
| + | *In order to be able to consider them in the usual way, a (equivalent) lowpass transformation is necessary. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Solution 1</u> is correct: | ||
| + | *The time signal is purely real, since the real part of the spectrum is even and the imaginary part is odd. | ||
| + | *This property is lost in bandpass systems, which must be transformed to the equivalent baseband, by cutting off the negative frequencies. The time signal thus becomes complex. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The corresponding bandwidths for the calculation can be read from the diagram: | ||
| + | :$$N_{{\rm{Up}}} = \frac{{276\,\,{\rm kHz}} -{138\,\,{\rm kHz}}} {{4.3125\,\,{\rm kHz}}}\hspace{0.15cm}\underline {= 32},$$ | ||
| + | :$$N_{{\rm{Down}}} = \frac{{1104\,\,{\rm kHz}} -{276\,\,{\rm kHz}}} {{4.3125\,\,{\rm kHz}}}\hspace{0.15cm}\underline {= 192}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' The core symbol duration is the reciprocal of the basic frequency: | ||
| + | :$$T = \frac{1} {f_0}= \frac{1} {{4.3125\,\,{\rm kHz}}} \hspace{0.15cm}\underline {\approx 232 \,\,{\rm µ s}}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' From this, the duration of the guard interval is: | ||
| + | :$$T_{\rm G} = \frac{N_{\rm G}} {N} \cdot T = \frac{32} {512} \cdot 232 \,\,{\rm µ s} \hspace{0.15cm}\underline {\approx 14 \,\,{\rm µ s}}.$$ | ||
| + | |||
| − | ''' | + | '''(6)''' A frame is composed of the core symbol and the cyclic prefix: |
| + | :$$T_{\rm R} = T + T_{\rm G}\hspace{0.15cm}\underline { ≈ 246 \ \rm µs}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(7)''' With parameters $N_{\rm Down} = 192$, $T_{\rm R} ≈ 246 \ \rm µ s$ and $M = 2$, we obtain: |
| − | $$ | + | :$$R_{\rm B,\, Down} = \frac{192 \cdot {{\rm{log}_2}(2)}}{246 \,\,{\rm µ s}} \cdot \frac {68}{69}\hspace{0.15cm}\underline {\approx 768 \,\,{\rm kbit/s}}.$$ |
| + | *It is taken into account here that every $69$th frame is only used for synchronization. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''8 | + | '''(8)''' For the DMT spectrum, in general: |
| − | $$S | + | :$$S\big[(N - \mu ) \cdot f_0 \big ] = S^*(\mu \cdot f_0).$$ |
| − | + | *Thus, with $N = 512$ and $S(198 · f_0) = 1 + 3 · {\rm j}$ holds: | |
| − | $$S(314 \cdot f_0) \hspace{0.15cm}\underline {= 1 | + | :$$S(314 \cdot f_0) = 1 - 3 \cdot {\rm j}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text{Re}[S(314 · f_0)]\hspace{0.15cm}\underline {= 1}, |
| + | \hspace{0.3cm}\text{Im}[S(314 · f_0)]\hspace{0.15cm}\underline {= -3}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 100: | Line 126: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^5.8 Further OFDM Applications^]] |
Latest revision as of 13:02, 25 January 2022
In this exercise we consider a $\rm DSL$ System ("Digital Subscriber Line"), where for modulation
- $\rm DMT$ ("Discrete Multitone Transmission")
- with $N = 512$ grid points
is used. In this context, the carriers are also referred to as "bins".
For DSL is specified:
- The carrier spacing is $f_0 = 4.3125\ \rm kHz$.
- For the spectrum holds: $S(f = 0) = 0$.
- The so-called "Nyquist tone" is also set to zero: $S(256 · f_0) = 0$.
The diagram shows the bandwidth organization of the considered system for positive frequencies:
- A transmission frame of $\rm DMT$ is composed of the core symbol duration $T$ and the duration $T_{\rm G}$ of the cyclic prefix, as in OFDM. This consists of $N_{\rm G} = 32$ samples.
- For synchronization between transmitter and receiver, a synchronization frame is sent after every $68$ frames, which does not contain any user data.
Notes:
- The exercise belongs to the chapter Further OFDM Applications.
- Reference is made in particular to the sections A brief description of DSL and Differences between DMT and the described OFDM.
- For more information on the topic, refer to the second chapter: $\rm DSL$ – "Digital Subscriber Line" of the LNTwww book Examples of Communication Systems.
Questions
Solution
- DSL is a baseband system.
- In contrast, mobile radio systems are bandpass systems which are operated in correspondingly high frequency ranges.
- In order to be able to consider them in the usual way, a (equivalent) lowpass transformation is necessary.
(2) Solution 1 is correct:
- The time signal is purely real, since the real part of the spectrum is even and the imaginary part is odd.
- This property is lost in bandpass systems, which must be transformed to the equivalent baseband, by cutting off the negative frequencies. The time signal thus becomes complex.
(3) The corresponding bandwidths for the calculation can be read from the diagram:
- $$N_{{\rm{Up}}} = \frac{{276\,\,{\rm kHz}} -{138\,\,{\rm kHz}}} {{4.3125\,\,{\rm kHz}}}\hspace{0.15cm}\underline {= 32},$$
- $$N_{{\rm{Down}}} = \frac{{1104\,\,{\rm kHz}} -{276\,\,{\rm kHz}}} {{4.3125\,\,{\rm kHz}}}\hspace{0.15cm}\underline {= 192}.$$
(4) The core symbol duration is the reciprocal of the basic frequency:
- $$T = \frac{1} {f_0}= \frac{1} {{4.3125\,\,{\rm kHz}}} \hspace{0.15cm}\underline {\approx 232 \,\,{\rm µ s}}.$$
(5) From this, the duration of the guard interval is:
- $$T_{\rm G} = \frac{N_{\rm G}} {N} \cdot T = \frac{32} {512} \cdot 232 \,\,{\rm µ s} \hspace{0.15cm}\underline {\approx 14 \,\,{\rm µ s}}.$$
(6) A frame is composed of the core symbol and the cyclic prefix:
- $$T_{\rm R} = T + T_{\rm G}\hspace{0.15cm}\underline { ≈ 246 \ \rm µs}.$$
(7) With parameters $N_{\rm Down} = 192$, $T_{\rm R} ≈ 246 \ \rm µ s$ and $M = 2$, we obtain:
- $$R_{\rm B,\, Down} = \frac{192 \cdot {{\rm{log}_2}(2)}}{246 \,\,{\rm µ s}} \cdot \frac {68}{69}\hspace{0.15cm}\underline {\approx 768 \,\,{\rm kbit/s}}.$$
- It is taken into account here that every $69$th frame is only used for synchronization.
(8) For the DMT spectrum, in general:
- $$S\big[(N - \mu ) \cdot f_0 \big ] = S^*(\mu \cdot f_0).$$
- Thus, with $N = 512$ and $S(198 · f_0) = 1 + 3 · {\rm j}$ holds:
- $$S(314 \cdot f_0) = 1 - 3 \cdot {\rm j}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text{Re}[S(314 · f_0)]\hspace{0.15cm}\underline {= 1}, \hspace{0.3cm}\text{Im}[S(314 · f_0)]\hspace{0.15cm}\underline {= -3}.$$