Difference between revisions of "Aufgaben:Exercise 2.8: COST Delay Models"
m (Text replacement - "power spectral density" to "power-spectral density") |
|||
| (17 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/The_GWSSUS_Channel_Model}} |
| − | [[File:Mob_A_2_8_version2.png|right|frame| | + | [[File:Mob_A_2_8_version2.png|right|frame|COST delay models]] |
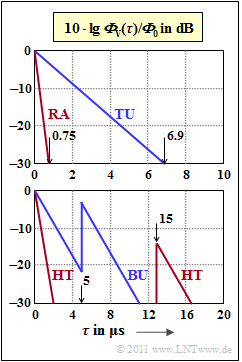
On the right, four delay power density spectra are plotted logarithmically as a function of the delay time $\tau$ | On the right, four delay power density spectra are plotted logarithmically as a function of the delay time $\tau$ | ||
| − | :$$10 \cdot {\rm lg}\hspace{0.15cm} ({{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0}) \hspace{0.05cm} | + | :$$10 \cdot {\rm lg}\hspace{0.15cm} ({{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0}) \hspace{0.05cm}.$$ |
| − | Here the abbreviation $\phi_0 = \phi_{\rm V}(\tau = 0)$ is used. These are the so-called | + | Here the abbreviation $\phi_0 = \phi_{\rm V}(\tau = 0)$ is used. These are the so-called COST delay models. |
| − | The upper sketch contains the two profiles ${\rm RA}$ ( | + | The upper sketch contains the two profiles ${\rm RA}$ ("Rural Area") and ${\rm TU}$ ("Typical Urban"). Both of these are exponential: |
:$${{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.05cm}.$$ | :$${{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.05cm}.$$ | ||
| − | The value of the parameter $\tau_0$ (time constant of the | + | The value of the parameter $\tau_0$ (time constant of the auto-correlation function) should be determined from the graphic in subtask '''(1)'''. Note the specified values of $\tau_{-30}$ for ${\it \Phi}_{\rm V}(\tau_{-30})=-30 \ \rm dB$: |
:$${\rm RA}\text{:}\hspace{0.15cm}\tau_{-30} = 0.75\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm} | :$${\rm RA}\text{:}\hspace{0.15cm}\tau_{-30} = 0.75\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm} | ||
{\rm TU}\text{:}\hspace{0.15cm}\tau_{-30} = 6.9\,{\rm µ s} \hspace{0.05cm}. $$ | {\rm TU}\text{:}\hspace{0.15cm}\tau_{-30} = 6.9\,{\rm µ s} \hspace{0.05cm}. $$ | ||
The lower graph applies to less favourable conditions in | The lower graph applies to less favourable conditions in | ||
| − | * urban areas ( | + | * urban areas ("Bad Urban", ${\rm BU}$): |
:$${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} | :$${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} | ||
= \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ | = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ | ||
| Line 23: | Line 23: | ||
\\ \hspace{-0.15cm} {\,\, \,\, \rm if}\hspace{0.15cm}5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}, \end{array}$$ | \\ \hspace{-0.15cm} {\,\, \,\, \rm if}\hspace{0.15cm}5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}, \end{array}$$ | ||
| − | * in rural areas ( | + | * in rural areas ("Hilly Terrain", ${\rm HT}$): |
:$${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} | :$${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} | ||
= \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ | = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ | ||
| Line 30: | Line 30: | ||
\\ \hspace{-0.35cm} {\rm if}\hspace{0.15cm}15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \end{array}$$ | \\ \hspace{-0.35cm} {\rm if}\hspace{0.15cm}15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \end{array}$$ | ||
| − | For the models | + | For the models ${\rm RA}$, ${\rm TU}$ and ${\rm BU}$ the following parameters are to be determined: |
| − | * The <b>delay spread</b> $T_{\rm V}$ is the standard deviation of the delay $\tau$. <br>If the | + | * The <b>delay spread</b> $T_{\rm V}$ is the standard deviation of the delay $\tau$. <br>If the delay power-spectral density ${\it \Phi}_{\rm V}(\tau)$ has an exponential course as with the profiles ${\rm RA}$ and ${\rm TU}$, then $T_{\rm V} = \tau_0$, see [[Aufgaben:Exercise_2.7:_Coherence_Bandwidth|Exercise 2.7]]. |
| − | * The <b>coherence bandwidth</b> $B_{\rm K}$ is the value of $\Delta f$ at which the magnitude of the frequency correlation function $\varphi_{\rm F}(\Delta f)$ has dropped to half its value for the first time. With exponential ${\it \Phi}_{\rm V}(\tau)$ as with ${\rm RA}$ and ${\rm TU}$ the product $T_{\rm V} | + | * The <b>coherence bandwidth</b> $B_{\rm K}$ is the value of $\Delta f$ at which the magnitude of the frequency correlation function $\varphi_{\rm F}(\Delta f)$ has dropped to half its value for the first time. With exponential ${\it \Phi}_{\rm V}(\tau)$ as with ${\rm RA}$ and ${\rm TU}$ the product is $T_{\rm V} \cdot B_{\rm K} \approx 0.276$, see [[Aufgaben:Exercise_2.7:_Coherence_Bandwidth|Exercise 2.7]]. |
| Line 41: | Line 41: | ||
''Notes:'' | ''Notes:'' | ||
| − | * This | + | *This exercise belongs to the chapter [[Mobile_Communications/The_GWSSUS_Channel_Model|The GWSSUS Channel Model]]. |
* The following integrals are given: | * The following integrals are given: | ||
:$$\frac{1}{\tau_0} \cdot \int_{0}^{\infty}\hspace{-0.15cm} {\rm e}^{ -\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = 1 | :$$\frac{1}{\tau_0} \cdot \int_{0}^{\infty}\hspace{-0.15cm} {\rm e}^{ -\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = 1 | ||
| Line 53: | Line 53: | ||
===Questionnaire=== | ===Questionnaire=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Specify the parameter $\tau_0$ of the delay power density | + | {Specify the parameter $\tau_0$ of the delay power-spectral density for the profiles ${\rm RA}$ and ${\rm TU}$ . |
|type="{}"} | |type="{}"} | ||
| − | ${\rm RA} \text \ \hspace{0.4cm} \tau_0 \ = \ ${ 0.109 3% } $\ \rm µ s$ | + | ${\rm RA} \text{:} \ \hspace{0.4cm} \tau_0 \ = \ ${ 0.109 3% } $\ \rm µ s$ |
| − | ${\rm TU} \text \ \hspace{0.4cm} \tau_0 \ = \ ${ 1 3% } $\ \rm µ s$ | + | ${\rm TU} \text{:} \ \hspace{0.4cm} \tau_0 \ = \ ${ 1 3% } $\ \rm µ s$ |
{How large is the delay spread $T_{\rm V}$ of these channels? | {How large is the delay spread $T_{\rm V}$ of these channels? | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm RA} \text \ \hspace{0.4cm} T_{\rm V} \ = \ ${ 0.109 3% } $\ \rm µ s$ | + | ${\rm RA} \text{:} \ \hspace{0.4cm} T_{\rm V} \ = \ ${ 0.109 3% } $\ \rm µ s$ |
| − | ${\rm TU} \text \ \hspace{0.4cm} T_{\rm V} \ = \ ${ 1 3% } $\ \rm µ s$ | + | ${\rm TU} \text{:} \ \hspace{0.4cm} T_{\rm V} \ = \ ${ 1 3% } $\ \rm µ s$ |
{What is the coherence bandwidth $B_{\rm K}$ of these channels? | {What is the coherence bandwidth $B_{\rm K}$ of these channels? | ||
| Line 69: | Line 69: | ||
{For which channel does frequency selectivity play a greater role? | {For which channel does frequency selectivity play a greater role? | ||
| − | |type=" | + | |type="()"} |
- Rural Area $({\rm RA})$. | - Rural Area $({\rm RA})$. | ||
+ Typical urban $({\rm TU})$. | + Typical urban $({\rm TU})$. | ||
| − | {How large is the (normalized) power density for & | + | {How large is the (normalized) power density for "Bad Urban" $({\rm BU})$ with $\tau = 5.001 \ \rm µ s$ and with $\tau = 4.999 \ \rm µ s$? |
|type="{}"} | |type="{}"} | ||
${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s) \ = \ ${ 0.5 3% } $\ \cdot {\it \Phi}_0$ | ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s) \ = \ ${ 0.5 3% } $\ \cdot {\it \Phi}_0$ | ||
| − | ${\it \Phi}_{\rm V}(\tau = 4 | + | ${\it \Phi}_{\rm V}(\tau = 4.999 \ \rm µ s) \ = \ ${ 0.00674 3% } $\ \cdot {\it \Phi}_0$ |
| − | {We consider ${\rm BU}$ again. Let $P_1$ be the power of the signal between $0$ and $5 \ \rm µ s$, and let $P_2$ be the remaining signal power. What percentage of the total signal power | + | {We consider ${\rm BU}$ again. Let $P_1$ be the power of the signal between $0$ and $5 \ \rm µ s$, and let $P_2$ be the remaining signal power. <br>What percentage of the total signal power comes from the interval |
| − | $P_1/(P_1 + P_2) \ = \ ${ 66.7 3% } $ | + | $0< t < 5 \ \rm µ s$? |
| + | |type="{}"} | ||
| + | $P_1/(P_1 + P_2) \ = \ ${ 66.7 3% } $\ \rm \%$ | ||
| − | {Calculate the delay spread $T_{\rm V}$ of the profile ${\rm BU}$. ''Note'': The average delay is $m_{\rm V} = E[\tau] = 2.667 \ \rm µ s$. | + | {Calculate the delay spread $T_{\rm V}$ of the profile ${\rm BU}$. <br>''Note'': The average delay is $m_{\rm V} = E[\tau] = 2.667 \ \rm µ s$. |
|type="{}"} | |type="{}"} | ||
$T_{\rm V} \ = \ ${ 2.56 3% } $\ \rm µ s$ | $T_{\rm V} \ = \ ${ 2.56 3% } $\ \rm µ s$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' The following property can be seen from the graph: | '''(1)''' The following property can be seen from the graph: | ||
| Line 97: | Line 99: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Here $\tau_{-30}$ denotes the delay that leads to the logarithmic ordinate value $-30 \ \rm dB$. Thus one obtains | + | Here $\tau_{-30}$ denotes the delay that leads to the logarithmic ordinate value $-30 \ \rm dB$. Thus one obtains |
| − | * for | + | * for "Rural Area" $\rm (RA)$ with $\tau_{–30} = 0.75 \ \rm µ s$: |
| − | :$$\tau_{\rm 0} = \frac{0.75\,{\rm | + | :$$\tau_{\rm 0} = \frac{0.75\,{\rm µ s}}{ 6.9} \hspace{0.1cm}\underline {\approx 0.109\,{\rm µ s}} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * for urban and suburban areas | + | * for urban and suburban areas ⇒ "Typical Urban" $\rm (TU)$ with $\tau_{–30} = 6.9 \ \rm µ s$: |
| − | :$$\tau_{\rm 0} = \frac{6.9\,{\rm | + | :$$\tau_{\rm 0} = \frac{6.9\,{\rm µ s}}{ 6.9} \hspace{0.1cm}\underline {\approx 1\,{\rm µ s}} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | '''(2)''' In [[Aufgaben:Exercise_2.7:_Coherence_Bandwidth|Exercise 2.7]], it was shown that the delay spread is $T_{\rm V} =\tau_0$ when the delay power density | + | '''(2)''' In [[Aufgaben:Exercise_2.7:_Coherence_Bandwidth|Exercise 2.7]], it was shown that the delay spread is $T_{\rm V} =\tau_0$ when the delay power-spectral density decreases exponentially according to ${\rm e}^{-\tau/\tau_0}$. Thus the following applies: |
| − | * for | + | * for "Rural Area": $\hspace{0.4cm} T_{\rm V} \ \underline {= 0.109 \ \rm µ s}$, |
| − | * for | + | * for "Typical Urban": $\hspace{0.4cm} T_{\rm V} \ \underline {= 1 \ \rm µ s}$. |
| − | '''(3)''' In | + | '''(3)''' In Exercise 2.7 it was also shown that for the coherence bandwidth $B_{\rm K} \approx 0.276/\tau_0$ applies. It follows: |
| − | *$B_{\rm K} \ \underline {\approx 2500 \ \rm kHz}$ ( | + | *$B_{\rm K} \ \underline {\approx 2500 \ \rm kHz}$ ("Rural Area"), |
| − | * $B_{\rm K} \ \underline {\approx 276 \ \ \rm kHz}$ ( | + | *$B_{\rm K} \ \underline {\approx 276 \ \ \rm kHz}$ ("Typical Urban") |
| Line 120: | Line 122: | ||
'''(4)''' The <u>second solution</u> is correct: | '''(4)''' The <u>second solution</u> is correct: | ||
| − | *Frequency selectivity of the mobile radio channel is present if the signal bandwidth $B_{\rm S}$ is larger than the coherence bandwidth $B_{\rm K}$ (or at least of the same order of magnitude). | + | *Frequency selectivity of the mobile radio channel is present if the signal bandwidth $B_{\rm S}$ is larger than the coherence bandwidth $B_{\rm K}$ (or at least of the same order of magnitude). |
| − | *The smaller $B_{\rm K}$ is, the more often this happens. | + | *The smaller $B_{\rm K}$ is, the more often this happens. |
| − | '''(5)''' According to the given equation, we have ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s)/{\it \Phi}_0 \hspace{0.15cm}\underline{\approx0.5}$. | + | '''(5)''' According to the given equation, we have ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s)/{\it \Phi}_0 \hspace{0.15cm}\underline{\approx0.5}$. |
| − | *On the other hand, for slightly smaller $\tau$ (for example $\tau = 4 | + | *On the other hand, for slightly smaller $\tau$ $($for example $\tau = 4.999 \ \rm µ s)$ we have approximately |
:$${{\it \Phi}_{\rm V}(\tau = 4.999\,{\rm \mu s})}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -{4.999\,{\rm µ s}}/{ 1\,{\rm \mu s}}} | :$${{\it \Phi}_{\rm V}(\tau = 4.999\,{\rm \mu s})}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -{4.999\,{\rm µ s}}/{ 1\,{\rm \mu s}}} | ||
\approx {\rm e}^{-5} \hspace{0.1cm}\underline {= 0.00674 }\hspace{0.05cm}.$$ | \approx {\rm e}^{-5} \hspace{0.1cm}\underline {= 0.00674 }\hspace{0.05cm}.$$ | ||
| − | '''(6)''' The power $P_1$ of all signal components with delays between $0$ and $5 \ | + | '''(6)''' The power $P_1$ of all signal components with delays between $0$ and $5 \ µ\rm s$ is: |
:$$P_1 = {\it \Phi}_{\rm 0} \cdot \int_{0}^{5\,{\rm \mu s}} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} | :$$P_1 = {\it \Phi}_{\rm 0} \cdot \int_{0}^{5\,{\rm \mu s}} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} | ||
{\it \Phi}_{\rm 0} \cdot \int_{0}^{\infty} {\rm e}^{ -{\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau | {\it \Phi}_{\rm 0} \cdot \int_{0}^{\infty} {\rm e}^{ -{\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau | ||
= {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$ | = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$ | ||
| − | *The power outside $[0\; | + | *The power outside $[0\;µ \mathrm{s}, 5\;µ \mathrm{s}]$ is |
:$$P_2 = \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{5\,{\rm µ s}}^{\infty} {\rm exp}[ \frac{5\,{\rm µ s} -\tau}{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} | :$$P_2 = \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{5\,{\rm µ s}}^{\infty} {\rm exp}[ \frac{5\,{\rm µ s} -\tau}{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} | ||
\frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{0}^{\infty} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau | \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{0}^{\infty} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau | ||
= \frac{{\it \Phi}_{\rm 0} \cdot \tau_0}{2} \hspace{0.05cm}. $$ | = \frac{{\it \Phi}_{\rm 0} \cdot \tau_0}{2} \hspace{0.05cm}. $$ | ||
| − | |||
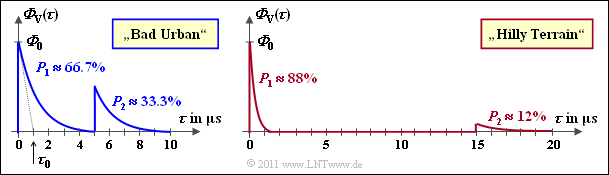
[[File:P_ID2184__Mob_A_2_8f.png|right|frame|Delay power density of the COST profiles ${\rm BU}$ and ${\rm HT}$]] | [[File:P_ID2184__Mob_A_2_8f.png|right|frame|Delay power density of the COST profiles ${\rm BU}$ and ${\rm HT}$]] | ||
| + | |||
| + | *Correspondingly, the percentage of power between $0$ and $5 \ µ\rm s$ is | ||
:$$\frac{P_1}{P_1+ P_2} = \frac{2}{3} \hspace{0.15cm}\underline {\approx 66.7\%}\hspace{0.05cm}.$$ | :$$\frac{P_1}{P_1+ P_2} = \frac{2}{3} \hspace{0.15cm}\underline {\approx 66.7\%}\hspace{0.05cm}.$$ | ||
| − | The figure shows ${\it \Phi}_{\rm V}(\tau)$ in linear scale | + | The figure shows ${\it \Phi}_{\rm V}(\tau)$ in linear scale. The areas $P_1$ and $P_2$ are labeled. |
| − | |||
*The left graph is for ${\rm BU}$, the right graph is for ${\rm HT}$. | *The left graph is for ${\rm BU}$, the right graph is for ${\rm HT}$. | ||
| − | *For the latter, the power percentage of all later echoes (later than $15 \ \rm µ s$ | + | *For the latter, the power percentage of all later echoes $($later than $15 \ \rm µ s)$ is only about $12\%$. |
<br clear=all> | <br clear=all> | ||
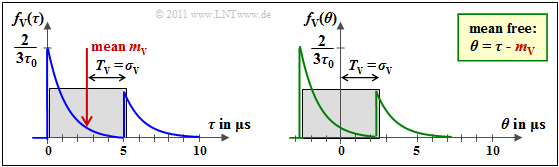
| − | '''(7)''' The area of the entire power density | + | '''(7)''' The area of the entire power-spectral density gives $P = 1.5 \cdot \phi_0 \cdot \tau_0$. |
| − | + | [[File:EN_Mob_A_2_8.png|right|frame|Delay PDF of profile ${\rm BU}$ ]] | |
| − | + | *Normalizing ${\it \Phi}_{\rm V}(\tau)$ to this value yields the probability density function $f_{\rm V}(\tau)$, as shown in the graph on the right (left diagram). | |
| − | *With $\tau_0 = 1 \ \ \rm µ s$ and $\tau_5 = 5 \ \ \rm µ s$, the mean is: | + | *With $\tau_0 = 1 \ \ \rm µ s$ and $\tau_5 = 5 \ \ \rm µ s$, the mean is: |
:$$m_{\rm V}= \int_{0}^{\infty} f_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau$$ | :$$m_{\rm V}= \int_{0}^{\infty} f_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau$$ | ||
:$$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2}{3\tau_0} \cdot \int_{0}^{\tau_5} \tau \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau \ + $$ | :$$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2}{3\tau_0} \cdot \int_{0}^{\tau_5} \tau \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau \ + $$ | ||
:$$ \hspace{1.7cm}+\ \frac{1}{3\tau_0} \cdot \int_{\tau_5}^{\infty} \tau \cdot {\rm e}^{ (\tau_5 -\tau)/\tau_0}\hspace{0.15cm}{\rm d} \tau \hspace{0.05cm}. $$ | :$$ \hspace{1.7cm}+\ \frac{1}{3\tau_0} \cdot \int_{\tau_5}^{\infty} \tau \cdot {\rm e}^{ (\tau_5 -\tau)/\tau_0}\hspace{0.15cm}{\rm d} \tau \hspace{0.05cm}. $$ | ||
| − | *The first integral is equal to $2\tau_0/3$ according to the provided expression. | + | *The first integral is equal to $2\tau_0/3$ according to the provided expression. |
| − | *With the substitution $\tau' = \tau \, -\tau_5$ you finally obtain using the integral solutions given above: | + | *With the substitution $\tau' = \tau \, -\tau_5$ you finally obtain using the integral solutions given above: |
:$$m_{\rm V} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2\tau_0}{3} + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau') \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' = \frac{2\tau_0}{3} + | :$$m_{\rm V} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2\tau_0}{3} + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau') \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' = \frac{2\tau_0}{3} + | ||
\frac{\tau_5}{3\tau_0} \cdot \int_{0}^{\infty} \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + | \frac{\tau_5}{3\tau_0} \cdot \int_{0}^{\infty} \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + | ||
| Line 170: | Line 172: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | *The variance $\sigma_{\rm V}^2$ is equal to the second moment (mean of the square) of the zero-mean random variable $\theta = \tau \, –m_{\rm V}$, whose PDF is shown in the right graph | + | *The variance $\sigma_{\rm V}^2$ is equal to the second moment (mean of the square) of the zero-mean random variable $\theta = \tau \, –m_{\rm V}$, whose PDF is shown in the right graph |
| − | *From this $T_{\rm V} = \sigma_{\rm V}$ can be specified. | + | *From this $T_{\rm V} = \sigma_{\rm V}$ can be specified. |
| + | |||
| − | + | A second possibility is to first calculate the mean square value of the random variable $\tau$ and from this the variance $\sigma_{\rm V}^2$ using Steiner's theorem. | |
*With the substitutions and approximations already described above, one obtains | *With the substitutions and approximations already described above, one obtains | ||
:$$m_{\rm V2} \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{2}{3\tau_0} \cdot \int_{0}^{\infty} \tau^2 \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau')^2 \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$ | :$$m_{\rm V2} \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{2}{3\tau_0} \cdot \int_{0}^{\infty} \tau^2 \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau')^2 \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$ | ||
| Line 186: | Line 189: | ||
:$$\Rightarrow \hspace{0.3cm} T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {\approx 2.56\,{\rm µ s}}\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {\approx 2.56\,{\rm µ s}}\hspace{0.05cm}.$$ | ||
| − | The above graph shows the parameters $T_{\rm V}$ and $\sigma_{\rm V}$. | + | The above graph shows the parameters $T_{\rm V}$ and $\sigma_{\rm V}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^2.3 The GWSSUS Channel Model^]] |
Latest revision as of 12:41, 17 February 2022
On the right, four delay power density spectra are plotted logarithmically as a function of the delay time $\tau$
- $$10 \cdot {\rm lg}\hspace{0.15cm} ({{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0}) \hspace{0.05cm}.$$
Here the abbreviation $\phi_0 = \phi_{\rm V}(\tau = 0)$ is used. These are the so-called COST delay models.
The upper sketch contains the two profiles ${\rm RA}$ ("Rural Area") and ${\rm TU}$ ("Typical Urban"). Both of these are exponential:
- $${{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.05cm}.$$
The value of the parameter $\tau_0$ (time constant of the auto-correlation function) should be determined from the graphic in subtask (1). Note the specified values of $\tau_{-30}$ for ${\it \Phi}_{\rm V}(\tau_{-30})=-30 \ \rm dB$:
- $${\rm RA}\text{:}\hspace{0.15cm}\tau_{-30} = 0.75\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm} {\rm TU}\text{:}\hspace{0.15cm}\tau_{-30} = 6.9\,{\rm µ s} \hspace{0.05cm}. $$
The lower graph applies to less favourable conditions in
- urban areas ("Bad Urban", ${\rm BU}$):
- $${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ 0.5 \cdot {\rm e}^{ (5\,{\rm \mu s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.55cm} {\rm if}\hspace{0.15cm}0 < \tau < 5\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}, \\ \hspace{-0.15cm} {\,\, \,\, \rm if}\hspace{0.15cm}5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}, \end{array}$$
- in rural areas ("Hilly Terrain", ${\rm HT}$):
- $${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ {0.04 \cdot \rm e}^{ (15\,{\rm \mu s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.55cm} {\rm if}\hspace{0.15cm}0 < \tau < 2\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm µ s} \hspace{0.05cm}, \\ \hspace{-0.35cm} {\rm if}\hspace{0.15cm}15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \end{array}$$
For the models ${\rm RA}$, ${\rm TU}$ and ${\rm BU}$ the following parameters are to be determined:
- The delay spread $T_{\rm V}$ is the standard deviation of the delay $\tau$.
If the delay power-spectral density ${\it \Phi}_{\rm V}(\tau)$ has an exponential course as with the profiles ${\rm RA}$ and ${\rm TU}$, then $T_{\rm V} = \tau_0$, see Exercise 2.7.
- The coherence bandwidth $B_{\rm K}$ is the value of $\Delta f$ at which the magnitude of the frequency correlation function $\varphi_{\rm F}(\Delta f)$ has dropped to half its value for the first time. With exponential ${\it \Phi}_{\rm V}(\tau)$ as with ${\rm RA}$ and ${\rm TU}$ the product is $T_{\rm V} \cdot B_{\rm K} \approx 0.276$, see Exercise 2.7.
Notes:
- This exercise belongs to the chapter The GWSSUS Channel Model.
- The following integrals are given:
- $$\frac{1}{\tau_0} \cdot \int_{0}^{\infty}\hspace{-0.15cm} {\rm e}^{ -\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = 1 \hspace{0.05cm},\hspace{0.6cm} \frac{1}{\tau_0} \cdot \int_{0}^{\infty}\hspace{-0.15cm} {\tau} \cdot{\rm e}^{ -\tau / \tau_0}\hspace{0.15cm}{\rm d} \tau = \tau_0 \hspace{0.05cm},\hspace{0.6cm} \frac{1}{\tau_0} \cdot \int_{0}^{\infty} \hspace{-0.15cm}{\tau^2} \cdot{\rm e}^{ -\tau / \tau_0}\hspace{0.15cm}{\rm d} \tau = 2\tau_0^2\hspace{0.05cm}.$$
Questionnaire
Solution
- $$10 \cdot {\rm lg}\hspace{0.1cm} (\frac{{\it \Phi}_{\rm V}(\tau_{\rm -30})}{{\it \Phi}_0}) = 10 \cdot {\rm lg}\hspace{0.1cm}\left [{\rm exp}[ -\frac{\tau_{\rm -30}}{ \tau_{\rm 0}}]\right ] \stackrel {!}{=} -30\,{\rm dB}$$
- $$\Rightarrow \hspace{0.3cm} {\rm lg}\hspace{0.1cm}\left [{\rm exp}[ -\frac{\tau_{\rm -30}}{ \tau_{\rm 0}}]\right ] = -3 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm ln}\hspace{0.1cm}\left [{\rm exp}[ -\frac{\tau_{\rm -30}}{ \tau_{\rm 0}}]\right ] = -3 \cdot {\rm ln}\hspace{0.1cm}(10)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \tau_{\rm 0} = \frac{\tau_{\rm -30}}{ 3 \cdot {\rm ln}\hspace{0.1cm}(10)}\approx \frac{\tau_{\rm -30}}{ 6.9} \hspace{0.05cm}.$$
Here $\tau_{-30}$ denotes the delay that leads to the logarithmic ordinate value $-30 \ \rm dB$. Thus one obtains
- for "Rural Area" $\rm (RA)$ with $\tau_{–30} = 0.75 \ \rm µ s$:
- $$\tau_{\rm 0} = \frac{0.75\,{\rm µ s}}{ 6.9} \hspace{0.1cm}\underline {\approx 0.109\,{\rm µ s}} \hspace{0.05cm},$$
- for urban and suburban areas ⇒ "Typical Urban" $\rm (TU)$ with $\tau_{–30} = 6.9 \ \rm µ s$:
- $$\tau_{\rm 0} = \frac{6.9\,{\rm µ s}}{ 6.9} \hspace{0.1cm}\underline {\approx 1\,{\rm µ s}} \hspace{0.05cm},$$
(2) In Exercise 2.7, it was shown that the delay spread is $T_{\rm V} =\tau_0$ when the delay power-spectral density decreases exponentially according to ${\rm e}^{-\tau/\tau_0}$. Thus the following applies:
- for "Rural Area": $\hspace{0.4cm} T_{\rm V} \ \underline {= 0.109 \ \rm µ s}$,
- for "Typical Urban": $\hspace{0.4cm} T_{\rm V} \ \underline {= 1 \ \rm µ s}$.
(3) In Exercise 2.7 it was also shown that for the coherence bandwidth $B_{\rm K} \approx 0.276/\tau_0$ applies. It follows:
- $B_{\rm K} \ \underline {\approx 2500 \ \rm kHz}$ ("Rural Area"),
- $B_{\rm K} \ \underline {\approx 276 \ \ \rm kHz}$ ("Typical Urban")
(4) The second solution is correct:
- Frequency selectivity of the mobile radio channel is present if the signal bandwidth $B_{\rm S}$ is larger than the coherence bandwidth $B_{\rm K}$ (or at least of the same order of magnitude).
- The smaller $B_{\rm K}$ is, the more often this happens.
(5) According to the given equation, we have ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s)/{\it \Phi}_0 \hspace{0.15cm}\underline{\approx0.5}$.
- On the other hand, for slightly smaller $\tau$ $($for example $\tau = 4.999 \ \rm µ s)$ we have approximately
- $${{\it \Phi}_{\rm V}(\tau = 4.999\,{\rm \mu s})}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -{4.999\,{\rm µ s}}/{ 1\,{\rm \mu s}}} \approx {\rm e}^{-5} \hspace{0.1cm}\underline {= 0.00674 }\hspace{0.05cm}.$$
(6) The power $P_1$ of all signal components with delays between $0$ and $5 \ µ\rm s$ is:
- $$P_1 = {\it \Phi}_{\rm 0} \cdot \int_{0}^{5\,{\rm \mu s}} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} {\it \Phi}_{\rm 0} \cdot \int_{0}^{\infty} {\rm e}^{ -{\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$
- The power outside $[0\;µ \mathrm{s}, 5\;µ \mathrm{s}]$ is
- $$P_2 = \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{5\,{\rm µ s}}^{\infty} {\rm exp}[ \frac{5\,{\rm µ s} -\tau}{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{0}^{\infty} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau = \frac{{\it \Phi}_{\rm 0} \cdot \tau_0}{2} \hspace{0.05cm}. $$
- Correspondingly, the percentage of power between $0$ and $5 \ µ\rm s$ is
- $$\frac{P_1}{P_1+ P_2} = \frac{2}{3} \hspace{0.15cm}\underline {\approx 66.7\%}\hspace{0.05cm}.$$
The figure shows ${\it \Phi}_{\rm V}(\tau)$ in linear scale. The areas $P_1$ and $P_2$ are labeled.
- The left graph is for ${\rm BU}$, the right graph is for ${\rm HT}$.
- For the latter, the power percentage of all later echoes $($later than $15 \ \rm µ s)$ is only about $12\%$.
(7) The area of the entire power-spectral density gives $P = 1.5 \cdot \phi_0 \cdot \tau_0$.
- Normalizing ${\it \Phi}_{\rm V}(\tau)$ to this value yields the probability density function $f_{\rm V}(\tau)$, as shown in the graph on the right (left diagram).
- With $\tau_0 = 1 \ \ \rm µ s$ and $\tau_5 = 5 \ \ \rm µ s$, the mean is:
- $$m_{\rm V}= \int_{0}^{\infty} f_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau$$
- $$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2}{3\tau_0} \cdot \int_{0}^{\tau_5} \tau \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau \ + $$
- $$ \hspace{1.7cm}+\ \frac{1}{3\tau_0} \cdot \int_{\tau_5}^{\infty} \tau \cdot {\rm e}^{ (\tau_5 -\tau)/\tau_0}\hspace{0.15cm}{\rm d} \tau \hspace{0.05cm}. $$
- The first integral is equal to $2\tau_0/3$ according to the provided expression.
- With the substitution $\tau' = \tau \, -\tau_5$ you finally obtain using the integral solutions given above:
- $$m_{\rm V} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2\tau_0}{3} + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau') \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' = \frac{2\tau_0}{3} + \frac{\tau_5}{3\tau_0} \cdot \int_{0}^{\infty} \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} \tau' \cdot \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$
- $$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2\tau_0}{3} + \frac{\tau_5}{3}+ \frac{\tau_0}{3} = \tau_0 + \frac{\tau_5}{3} \hspace{0.15cm}\underline {\approx 2.667\,{\rm µ s}} \hspace{0.05cm}. $$
- The variance $\sigma_{\rm V}^2$ is equal to the second moment (mean of the square) of the zero-mean random variable $\theta = \tau \, –m_{\rm V}$, whose PDF is shown in the right graph
- From this $T_{\rm V} = \sigma_{\rm V}$ can be specified.
A second possibility is to first calculate the mean square value of the random variable $\tau$ and from this the variance $\sigma_{\rm V}^2$ using Steiner's theorem.
- With the substitutions and approximations already described above, one obtains
- $$m_{\rm V2} \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{2}{3\tau_0} \cdot \int_{0}^{\infty} \tau^2 \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau')^2 \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$
- $$\Rightarrow \hspace{0.3cm}m_{\rm V2} = \frac{2}{3} \cdot \int_{0}^{\infty} \frac{\tau^2}{\tau_0} \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{\tau_5^2}{3} \cdot \int_{0}^{\infty} \frac{1}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' +\frac{2\tau_5}{3} \cdot \int_{0}^{\infty} \frac{\tau '}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + \frac{1}{3} \cdot \int_{0}^{\infty} \frac{{\tau '}^2}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' \hspace{0.05cm}. $$
- With the integrals given above, we have
- $$m_{\rm V2} \approx \frac{2}{3} \cdot 2 \tau_0^2 + \frac{\tau_5^2}{3} \cdot 1 + \frac{2\tau_5}{3} \cdot \tau_0 + \frac{1}{3} \cdot 2 \tau_0^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} $$
- $$\Rightarrow \hspace{0.3cm} \sigma_{\rm V}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_{\rm V2} - m_{\rm V}^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} - (\tau_0 + \frac{\tau_5}{3})^2 =\tau_0^2 + \frac{2\tau_5^2}{9} = (1\,{\rm µ s})^2 + \frac{2\cdot (5\,{\rm µ s})^2}{9} = 6.55\,({\rm µ s})^2$$
- $$\Rightarrow \hspace{0.3cm} T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {\approx 2.56\,{\rm µ s}}\hspace{0.05cm}.$$
The above graph shows the parameters $T_{\rm V}$ and $\sigma_{\rm V}$.