Difference between revisions of "Aufgaben:Exercise 4.14Z: Offset QPSK vs. MSK"
m |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 38: | Line 38: | ||
*The associated phase function $ϕ(t)$ is determined in [[Aufgaben:Exercise_4.14:_Phase_Progression_of_the_MSK |Exercise 4.14]] , and is also based on the (normalized) MSK fundamental pulse: | *The associated phase function $ϕ(t)$ is determined in [[Aufgaben:Exercise_4.14:_Phase_Progression_of_the_MSK |Exercise 4.14]] , and is also based on the (normalized) MSK fundamental pulse: | ||
| − | :$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos (\pi/2 \cdot t/T ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{ | + | :$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos (\pi/2 \cdot t/T ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{otherwise}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm }. \\ \end{array}$$ |
Latest revision as of 16:49, 21 March 2022
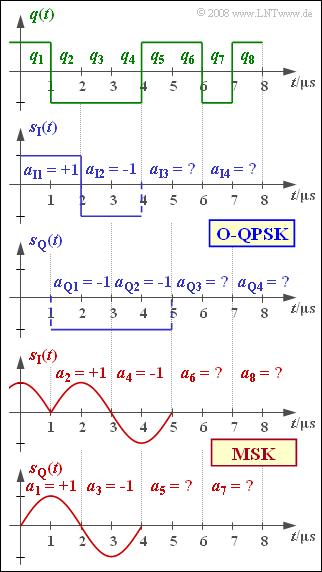
One possible implementation fordie $\rm MSK$ is offered by "Offset–QPSK" $\rm (O–QPSK)$, as can be seen from the block diagrams in the theory section.
In "normal offset QPSK operation", two bits of the source symbol sequence $〈q_k〉$ are assigned to one bit 𝑎Iν $a_{{\rm I}ν}$ in the in-phase branch and one bit $a_{{\rm Q}ν}$ in the quadrature branch, respectively.
The graph shows this serial-to-parallel conversion in the top three plots for the first four bits of the source signal $q(t)$. It should be noted:
- The Offset–QPSK plot is for for a rectangular-shaped fundamental pulse. The coefficients $a_{{\rm I}ν}$ and $a_{{\rm Q}ν}$ can take the values $±1$ .
- If the time index of the source symbols passes through the values $k =1,$ ... $, 8$, then the time variable $ν$ only takes on the values $1,$ ... $, 4$ an.
- The sketch also takes the time offset for the quadrature branch into account.
For a "MSK–implementation using Offset–QPSK" a recoding is required. Here, with $q_k ∈ \{+1, –1\}$ and $a_k ∈ \{+1, –1\}$, it holds that:
- $$a_k = (-1)^{k+1} \cdot a_{k-1} \cdot q_k \hspace{0.05cm}.$$
For example, by assuming $a_0 = +1$ one gets:
- $$a_1 = a_0 \cdot q_1 = +1,\hspace{0.4cm}a_2 = -a_1 \cdot q_2 = +1,\hspace{0.4cm} a_3 = a_2 \cdot q_3 = -1,\hspace{0.4cm}a_4 = -a_3 \cdot q_4 = -1 \hspace{0.05cm}.$$
Additionally, one must take into account:
- The coefficients $a_0 = +1$, $a_2 = +1$, $a_4 = -1$ and the coefficients $a_6$ and $a_8$ which are yet to be calculated, are assigned to the signal $s_{\rm I}(t)$ .
- On the other hand, the coefficients $a_1 = +1$ and $a_3 = -1$ as well as all other coefficients with an odd index are applied to the signal $s_{\rm Q}(t)$ .
Hints:
- This exercise belongs to the chapter Nonlinear Digital Modulation.
- Particular reference is made to the section Realizing MSK as Offset–QPSK.
- The associated phase function $ϕ(t)$ is determined in Exercise 4.14 , and is also based on the (normalized) MSK fundamental pulse:
- $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos (\pi/2 \cdot t/T ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{otherwise}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm }. \\ \end{array}$$
Questions
Solution
(2) For QPSK or offset QPSK , the symbol duration $T$ is twice the bit duration $T_{\rm B}$ due to serial-to-parallel conversion:
- $$ T = 2 \cdot T_{\rm B} \hspace{0.15cm}\underline {= 2\,{\rm µ s}} \hspace{0.05cm}.$$
(3) According to the allocation evident in the plot for the first bits:
- $$ a_{\rm I3} = q_5 \hspace{0.15cm}\underline {= +1},$$
- $$a_{\rm Q3} = q_6 \hspace{0.15cm}\underline {= +1},$$
- $$a_{\rm I4} = q_7 \hspace{0.15cm}\underline { = -1},$$
- $$a_{\rm Q4} = q_8 \hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
(4) In MSK, the symbol duration $T$ is equal to the bit duration $T_{\rm B}$:
- $$T = T_{\rm B}\hspace{0.15cm}\underline { = 1\,{\rm µ s}} \hspace{0.05cm}.$$
(5) According to the given recoding rule, when $a_4 = –1$, we get:
- $$q_5 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_5 = a_4 \cdot q_5 \hspace{0.15cm}\underline {= -1},$$
- $$q_6 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_6 = -a_5 \cdot q_6 \hspace{0.15cm}\underline {= +1},$$
- $$ q_7 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_7 = a_6 \cdot q_7 \hspace{0.15cm}\underline {= -1}, $$
- $$q_8 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_8 = -a_7 \cdot q_8\hspace{0.15cm}\underline { = +1}\hspace{0.05cm}.$$