Difference between revisions of "Aufgaben:Exercise 4.8Z: BPSK Error Probability"
| (One intermediate revision by the same user not shown) | |||
| Line 6: | Line 6: | ||
We assume the optimal baseband transmission system for binary signals with | We assume the optimal baseband transmission system for binary signals with | ||
* bipolar amplitude coefficients $a_ν ∈ \{-1, +1\}$, | * bipolar amplitude coefficients $a_ν ∈ \{-1, +1\}$, | ||
| − | * rectangular transmitted signal with signal values $±s_0$ and bit duration $T_{\rm B}$, | + | * rectangular transmitted signal $s(t)$ with signal values $±s_0$ and bit duration $T_{\rm B}$, |
* AWGN noise with the (one-sided) noise power density $N_0$, | * AWGN noise with the (one-sided) noise power density $N_0$, | ||
* receiver filter according to the matched filter principle, | * receiver filter according to the matched filter principle, | ||
| Line 12: | Line 12: | ||
| − | If nothing else is specified, you should assume the following numerical values: | + | If nothing else is specified, you should assume the following numerical values: |
:$$s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$ | :$$s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$ | ||
| − | Using the noise rms value $σ_d$ at the decision and the complementary Gaussian error function ${\rm Q}(x)$ the bit error probability of this baseband system is ⇒ see table: | + | Using the noise rms value $σ_d$ at the decision and the complementary Gaussian error function ${\rm Q}(x)$, the bit error probability of this baseband $\rm (BB)$ system is ⇒ see table: |
:$$ p_{\rm BB} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/(2 \cdot T_{\rm B}}).$$ | :$$ p_{\rm BB} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/(2 \cdot T_{\rm B}}).$$ | ||
This bit error probability can also be expressed in the form | This bit error probability can also be expressed in the form | ||
| − | :$$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )$$ | + | :$$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$ |
| − | where $E_{\rm B}$ indicates the "signal energy per bit". | + | where $E_{\rm B}$ indicates the "signal energy per bit". |
| − | The bit error probability of a comparable transmission system with | + | The bit error probability of a comparable transmission system with "Binary Phase Shift Keying" $\rm (BPSK)$ is: |
:$$ p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$ | :$$ p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$ | ||
| Line 28: | Line 28: | ||
| − | + | Notes: | |
| − | + | *The exercise belongs to the chapter [[Modulation_Methods/Linear_Digital_Modulation|"Linear Digital Modulation"]]. | |
| − | + | *Reference is made in particular to the section [[Modulation_Methods/Linear_Digital_Modulation#Error_probabilities_-_a_brief_overview|"Error probabilities - a brief overview"]]. | |
| − | *The exercise belongs to the chapter [[Modulation_Methods/Linear_Digital_Modulation|Linear Digital Modulation]]. | + | *The derivations can be found in the chapter [[Digital_Signal_Transmission/Lineare_digitale_Modulation_–_Kohärente_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]] of the book "Digital Signal Transmission". |
| − | *Reference is made in particular to the section [[Modulation_Methods/Linear_Digital_Modulation#Error_probabilities_-_a_brief_overview|Error probabilities - a brief overview]]. | ||
| − | *The derivations can be found in the chapter [[Digital_Signal_Transmission/Lineare_digitale_Modulation_–_Kohärente_Demodulation|Linear Digital Modulation - Coherent Demodulation]] of the book "Digital Signal Transmission". | ||
*The specification of a power in $\rm V^2$ or an energy in $\rm V^2 s$ means a conversion to the reference resistance $1 \ \rm \Omega$. | *The specification of a power in $\rm V^2$ or an energy in $\rm V^2 s$ means a conversion to the reference resistance $1 \ \rm \Omega$. | ||
| Line 48: | Line 46: | ||
| − | {For this set | + | {For this parameter set, what is the energy per bit ⇒ $E_{\rm B}$ for the baseband system? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 1.6 3% } $\ \cdot 10^{-8} \ \rm V^2 s$ | $E_{\rm B} \ = \ $ { 1.6 3% } $\ \cdot 10^{-8} \ \rm V^2 s$ | ||
| Line 62: | Line 60: | ||
- $p_{\rm BPSK} = {\rm Q}\big[(4E_{\rm B}/N_0)^{1/2}\big].$ | - $p_{\rm BPSK} = {\rm Q}\big[(4E_{\rm B}/N_0)^{1/2}\big].$ | ||
| − | {What are the error probabilities for BPSK | + | {What are the error probabilities for BPSK with $E_{\rm B}/N_0 = 8$ and $E_{\rm B}/N_0 = 2$? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B}/N_0 = 8\text{:} \ \ \ \ p_{\rm BPSK} \ = \ $ { 0.317 3% } $\ \cdot 10^{-4}$ | $E_{\rm B}/N_0 = 8\text{:} \ \ \ \ p_{\rm BPSK} \ = \ $ { 0.317 3% } $\ \cdot 10^{-4}$ | ||
| Line 80: | Line 78: | ||
'''(2)''' For the baseband system: | '''(2)''' For the baseband system: | ||
:$$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot 10^{-9}\,{\rm s}\hspace{0.15cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$ | :$$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot 10^{-9}\,{\rm s}\hspace{0.15cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$ | ||
| − | *Of course, the second equation | + | *Of course, the second equation gives the exact same error probability |
:$$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$ | :$$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$ | ||
| − | '''(3)''' When the transmitted amplitude is half $s_0 = 2\,{\rm V}$ the energy per bit decreases to one-fourth and the following equations apply: | + | '''(3)''' When the transmitted amplitude is half ⇒ $s_0 = 2\,{\rm V}$, the energy per bit decreases to one-fourth and the following equations apply: |
:$$ p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )= {\rm Q}(2)= 227 \cdot 10^{-4},$$ | :$$ p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )= {\rm Q}(2)= 227 \cdot 10^{-4},$$ | ||
:$$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)\hspace{0.15cm}\underline {= 227 \cdot 10^{-4}}.$$ | :$$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)\hspace{0.15cm}\underline {= 227 \cdot 10^{-4}}.$$ | ||
| − | '''(4)''' <u>Answer 2</u> is correct: | + | '''(4)''' <u>Answer 2</u> is correct: |
*Considering the energy $E_{\rm B} = s_0^2 · T_{\rm B}/2$ we obtain | *Considering the energy $E_{\rm B} = s_0^2 · T_{\rm B}/2$ we obtain | ||
:$$ p_{\rm BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }}\hspace{0.1cm}\right ).$$ | :$$ p_{\rm BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }}\hspace{0.1cm}\right ).$$ | ||
| − | *Thus, the same result is obtained as for the optimal baseband transmission system. | + | *Thus, the same result is obtained as for the optimal baseband transmission system. |
Latest revision as of 17:26, 15 April 2022
We assume the optimal baseband transmission system for binary signals with
- bipolar amplitude coefficients $a_ν ∈ \{-1, +1\}$,
- rectangular transmitted signal $s(t)$ with signal values $±s_0$ and bit duration $T_{\rm B}$,
- AWGN noise with the (one-sided) noise power density $N_0$,
- receiver filter according to the matched filter principle,
- decision with optimal threshold value $E = 0$.
If nothing else is specified, you should assume the following numerical values:
- $$s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$
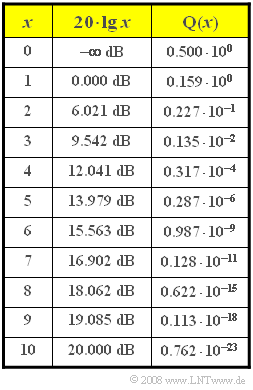
Using the noise rms value $σ_d$ at the decision and the complementary Gaussian error function ${\rm Q}(x)$, the bit error probability of this baseband $\rm (BB)$ system is ⇒ see table:
- $$ p_{\rm BB} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/(2 \cdot T_{\rm B}}).$$
This bit error probability can also be expressed in the form
- $$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$
where $E_{\rm B}$ indicates the "signal energy per bit".
The bit error probability of a comparable transmission system with "Binary Phase Shift Keying" $\rm (BPSK)$ is:
- $$ p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation".
- Reference is made in particular to the section "Error probabilities - a brief overview".
- The derivations can be found in the chapter "Linear Digital Modulation - Coherent Demodulation" of the book "Digital Signal Transmission".
- The specification of a power in $\rm V^2$ or an energy in $\rm V^2 s$ means a conversion to the reference resistance $1 \ \rm \Omega$.
Questions
Solution
- $$\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}= \sqrt{\frac{2 \cdot 10^{-9}\,{\rm V^2/Hz}}{2 \cdot 1\,{\rm ns}}}= 1\,{\rm V} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm BB} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )= {\rm Q}(4)\hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4}}.$$
(2) For the baseband system:
- $$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot 10^{-9}\,{\rm s}\hspace{0.15cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$
- Of course, the second equation gives the exact same error probability
- $$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$
(3) When the transmitted amplitude is half ⇒ $s_0 = 2\,{\rm V}$, the energy per bit decreases to one-fourth and the following equations apply:
- $$ p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )= {\rm Q}(2)= 227 \cdot 10^{-4},$$
- $$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)\hspace{0.15cm}\underline {= 227 \cdot 10^{-4}}.$$
(4) Answer 2 is correct:
- Considering the energy $E_{\rm B} = s_0^2 · T_{\rm B}/2$ we obtain
- $$ p_{\rm BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }}\hspace{0.1cm}\right ).$$
- Thus, the same result is obtained as for the optimal baseband transmission system.
(5) Exactly the same results are obtained as for the baseband transmission in questions (1) and (3):
- $${ E_{\rm B}}/{N_0 }= 8: \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{16}) = {\rm Q}(4)\hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4}},$$
- $$ { E_{\rm B}}/{N_0 }= 2: \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{4}) = {\rm Q}(2)\hspace{0.15cm}\underline {= 227 \cdot 10^{-4}}.$$