Difference between revisions of "Aufgaben:Exercise 4.9: Costas Rule Loop"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Lineare digitale Modulationsverfahren }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-C…“) |
|||
| (21 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Linear_Digital_Modulation |
}} | }} | ||
| − | [[File:|right|]] | + | [[File:EN_Mod_A_4_8.png|right|frame|Costas rule loop]] |
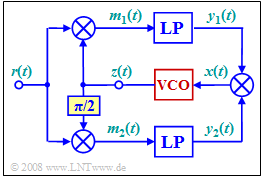
| + | An important prerequisite for coherent demodulation is "in-phase carrier recovery". One possibility for this is the so-called "Costas rule loop", which is shown in simplified form by the adjacent block diagram. | ||
| + | In binary phase modulation $\rm (BPSK)$, the received signal can be expressed as | ||
| + | :$$ r(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi)$$ | ||
| + | The phase rotation $ϕ$ on the transmission channel is always assumed to be unknown. The factor "±" describes the phase jumps of the BPSK signal. | ||
| − | === | + | The task of the circuit indicated by the diagram is to generate a carrier signal |
| + | :$$z(t) = \cos (2 \pi \cdot f_{\rm T} \cdot t + \theta)$$ | ||
| + | where the phase error $\phi - θ$ between the BPSK received signal $r(t)$ and the oscillation $z(t)$ generated at the receiver must be compensated. | ||
| + | *For this purpose, a "Voltage Controlled Oscillator" $($'''VCO'''$)$ is used to generate an oscillation of frequency $f_{\rm T}$, initially with arbitrary phase $θ$. | ||
| + | *However, the Costas rule loop iteratively achieves the desired result $θ = \phi$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Modulation_Methods/Linear_Digital_Modulation|"Linear Digital Modulation"]]. | ||
| + | *In the diagram, "TP" denotes low-passes (German: "Tiefpass" ⇒ subscript: "TP"), which are assumed to be ideal. | ||
| + | *The square labeled $π/2$ denotes a phase rotation by $π/2 \ (90^\circ)$, so that, for example, a cosine signal becomes a "minus-sine" signal: | ||
| + | :$$\cos (\omega_{\rm 0} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\cos (\omega_{\rm 0} \cdot t + 90^\circ) = -\sin (\omega_{\rm 0} \cdot t)\hspace{0.05cm}.$$ | ||
| + | *Further, the following trigonometric relations hold: | ||
| + | :$$\cos (\alpha) \cdot \cos (\beta) = {1} /{2} \cdot \big [ \cos (\alpha - \beta) + \cos (\alpha + \beta)\big]\hspace{0.05cm},$$ | ||
| + | :$$\sin (\alpha) \cdot \cos (\beta) = {1} /{2} \cdot \big [ \sin (\alpha - \beta) + \sin (\alpha + \beta)\big]\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the signal $y_1(t)$ after the low-pass in the upper branch. Which of the following statements is correct? |
| + | |type="()"} | ||
| + | - $y_1(t) = ± s_0/2 · \big[\cos (\phi - θ) + \cos (4 π · f_{\rm T} · t +\phi + θ)\big],$ | ||
| + | + $y_1(t) = ± s_0/2 · \cos (\phi - θ),$ | ||
| + | - $y_1(t) = ± s_0/2 · \sin (\phi - θ).$ | ||
| + | |||
| + | {Calculate the signal $y_2(t)$ after the low-pass in the lower branch. Which of the following statements is correct? | ||
| + | |type="()"} | ||
| + | - $y_2(t) = ± s_0/2 · \big[\cos (\phi - θ) + \cos (4 π · f_{\rm T} · t +\phi + θ)\big],$ | ||
| + | - $y_2(t) = ± s_0/2 · \cos (\phi - θ),$ | ||
| + | + $y_2(t) = ± s_0/2 · \sin (\phi - θ).$ | ||
| + | |||
| + | {Calculate the rule signal $x(t)$ and give an approximation for small phase deviation $\phi - θ$. Which equations are correct? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - $x(t) = s_0^2/8 · \cos(\phi + θ)$, |
| − | + | + | + $x(t) = s_0^2/8 · \sin(2 \phi - 2θ),$ |
| + | + $x(t) ≈ s_0^2/4 · (\phi - θ),$ | ||
| + | - $x(t) ≈ s_0^2/4 · (\phi - θ)^2.$ | ||
| − | { | + | </quiz> |
| − | + | ||
| − | $\ | + | ===Solution=== |
| + | {{ML-Kopf}} | ||
| + | '''(1)''' The <u>second solution</u> is correct: | ||
| + | *Using the addition theorem of trigonometry, we obtain: | ||
| + | :$$ m_1(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \theta) = \pm \frac{s_0}{2} \cdot \left [ \cos ( \phi - \theta) + \cos (4 \pi \cdot f_{\rm T} \cdot t + \phi +\theta)\right]\hspace{0.05cm}.$$ | ||
| + | *After the low-pass, only the DC component $y_1(t) = ± s_0/2 · \cos (\phi - θ)$ remains. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Here the <u>last solution</u> is correct: | ||
| + | *Analogous to question '''(1)''', the result for the input signal of the lower low-pass filter is: | ||
| + | :$$ m_2(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi) \cdot \left [-\sin (2 \pi \cdot f_{\rm T} \cdot t + \theta) \right]= \pm \frac{s_0}{2} \cdot \left [ \sin ( \phi - \theta) + \sin (4 \pi \cdot f_{\rm T} \cdot t + \phi +\theta)\right].$$ | ||
| + | *This leads to the following output signal: | ||
| + | :$$ y_2(t) = \pm {s_0}/{2} \cdot\sin ( \phi - \theta) \hspace{0.05cm}.$$ | ||
| − | </ | + | '''(3)''' <u>Solutions 2 and 3</u> are correct: |
| + | *By multiplying $y_1(t)$ and $y_2(t)$ we obtain: | ||
| + | :$$x(t) = y_1(t) \cdot y_2(t)= \frac{s_0^2}{4} \cdot \cos ( \phi - \theta) \cdot \sin ( \phi - \theta) | ||
| + | = \frac{s_0^2}{8} \cdot \sin ( 2\cdot\phi - 2\cdot\theta) \hspace{0.05cm}.$$ | ||
| + | *Using the small angle approximation $\sin(α) ≈ α$ it follows: | ||
| + | :$$x(t) \approx \frac{s_0^2}{4} \cdot ( \phi - \theta) \hspace{0.05cm}.$$ | ||
| + | *The rule signal $x(t)$ is thus proportional to the phase error $\phi - θ$, which is controlled to zero by the Costas rule loop. | ||
| + | *Thus, in the steady state, the oscillator signal $z(t)$ immediately follows the received signal $r(t)$. | ||
| + | *To achieve the required initial condition $θ ≈ \phi$, a training sequence is usually transmitted first and the phase is initialized accordingly. | ||
| + | *This is also because the phase is only controlled modulo $π$, so that, for example, $\phi - θ = π$ would incorrectly lead to the rule signal $x(t) = 0$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.2 Linear Digital Modulation^]] |
Latest revision as of 17:51, 15 April 2022
An important prerequisite for coherent demodulation is "in-phase carrier recovery". One possibility for this is the so-called "Costas rule loop", which is shown in simplified form by the adjacent block diagram.
In binary phase modulation $\rm (BPSK)$, the received signal can be expressed as
- $$ r(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi)$$
The phase rotation $ϕ$ on the transmission channel is always assumed to be unknown. The factor "±" describes the phase jumps of the BPSK signal.
The task of the circuit indicated by the diagram is to generate a carrier signal
- $$z(t) = \cos (2 \pi \cdot f_{\rm T} \cdot t + \theta)$$
where the phase error $\phi - θ$ between the BPSK received signal $r(t)$ and the oscillation $z(t)$ generated at the receiver must be compensated.
- For this purpose, a "Voltage Controlled Oscillator" $($VCO$)$ is used to generate an oscillation of frequency $f_{\rm T}$, initially with arbitrary phase $θ$.
- However, the Costas rule loop iteratively achieves the desired result $θ = \phi$.
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation".
- In the diagram, "TP" denotes low-passes (German: "Tiefpass" ⇒ subscript: "TP"), which are assumed to be ideal.
- The square labeled $π/2$ denotes a phase rotation by $π/2 \ (90^\circ)$, so that, for example, a cosine signal becomes a "minus-sine" signal:
- $$\cos (\omega_{\rm 0} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\cos (\omega_{\rm 0} \cdot t + 90^\circ) = -\sin (\omega_{\rm 0} \cdot t)\hspace{0.05cm}.$$
- Further, the following trigonometric relations hold:
- $$\cos (\alpha) \cdot \cos (\beta) = {1} /{2} \cdot \big [ \cos (\alpha - \beta) + \cos (\alpha + \beta)\big]\hspace{0.05cm},$$
- $$\sin (\alpha) \cdot \cos (\beta) = {1} /{2} \cdot \big [ \sin (\alpha - \beta) + \sin (\alpha + \beta)\big]\hspace{0.05cm}.$$
Questions
Solution
- Using the addition theorem of trigonometry, we obtain:
- $$ m_1(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \theta) = \pm \frac{s_0}{2} \cdot \left [ \cos ( \phi - \theta) + \cos (4 \pi \cdot f_{\rm T} \cdot t + \phi +\theta)\right]\hspace{0.05cm}.$$
- After the low-pass, only the DC component $y_1(t) = ± s_0/2 · \cos (\phi - θ)$ remains.
(2) Here the last solution is correct:
- Analogous to question (1), the result for the input signal of the lower low-pass filter is:
- $$ m_2(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi) \cdot \left [-\sin (2 \pi \cdot f_{\rm T} \cdot t + \theta) \right]= \pm \frac{s_0}{2} \cdot \left [ \sin ( \phi - \theta) + \sin (4 \pi \cdot f_{\rm T} \cdot t + \phi +\theta)\right].$$
- This leads to the following output signal:
- $$ y_2(t) = \pm {s_0}/{2} \cdot\sin ( \phi - \theta) \hspace{0.05cm}.$$
(3) Solutions 2 and 3 are correct:
- By multiplying $y_1(t)$ and $y_2(t)$ we obtain:
- $$x(t) = y_1(t) \cdot y_2(t)= \frac{s_0^2}{4} \cdot \cos ( \phi - \theta) \cdot \sin ( \phi - \theta) = \frac{s_0^2}{8} \cdot \sin ( 2\cdot\phi - 2\cdot\theta) \hspace{0.05cm}.$$
- Using the small angle approximation $\sin(α) ≈ α$ it follows:
- $$x(t) \approx \frac{s_0^2}{4} \cdot ( \phi - \theta) \hspace{0.05cm}.$$
- The rule signal $x(t)$ is thus proportional to the phase error $\phi - θ$, which is controlled to zero by the Costas rule loop.
- Thus, in the steady state, the oscillator signal $z(t)$ immediately follows the received signal $r(t)$.
- To achieve the required initial condition $θ ≈ \phi$, a training sequence is usually transmitted first and the phase is initialized accordingly.
- This is also because the phase is only controlled modulo $π$, so that, for example, $\phi - θ = π$ would incorrectly lead to the rule signal $x(t) = 0$.