Difference between revisions of "Aufgaben:Exercise 1.4Z: Complex Nyquist Spectrum"
| (19 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Properties_of_Nyquist_Systems |
}} | }} | ||
| − | [[File:P_ID1279__Dig_Z_1_4.png|right|frame| | + | [[File:P_ID1279__Dig_Z_1_4.png|right|frame|Complex Nyquist spectrum]] |
| − | + | Consider a pulse $g(t)$ with spectrum $G(f)$ according to the sketch. One recognizes from this representation: | |
| − | * | + | *The real part of $G(f)$ is trapezoidal with the corner frequencies $f_{1} = 3 \, \rm kHz$ and $f_{2} = 7 \, \rm kHz$. In the range $|f| < f_{1}$: |
| − | + | :$${\rm Re}\big[G(f)\big] = A = 10^{-4} \, \rm V/Hz.$$ | |
| − | * | + | *The imaginary part of $G(f)$ is always assumed to be ${\rm Im}\big[G(f)\big] =0$ for subtasks '''(1)''' to '''(5)'''. In this case $g(t)$ is certainly a Nyquist pulse. |
| − | * | + | *From subtask '''(6)''', the imaginary part ${\rm Im}[G(f)]$ in the range $f_{1} \leq | f | \leq f_{2}$ has a triangular shape with the values $\pm B$ at the triangle peaks. |
| − | + | ||
| + | |||
| + | It is necessary to check whether the pulse $g(t)$ satisfies the first Nyquist condition even with complex spectrum: | ||
:$$g(\nu | :$$g(\nu | ||
T) = \left\{ \begin{array}{c} g_0 \\ | T) = \left\{ \begin{array}{c} g_0 \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}} |
| − | \\ {\rm{ | + | \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} |
\nu = 0 \hspace{0.05cm}, \\ | \nu = 0 \hspace{0.05cm}, \\ | ||
\nu \ne 0 \hspace{0.1cm}. \\ | \nu \ne 0 \hspace{0.1cm}. \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | ||
| − | * | + | In the course of this exercise, reference is made to the following descriptive quantities: |
| + | *The '''Nyquist frequency''' gives the symmetry point of the rolloff: | ||
:$$f_{\rm Nyq}= \frac{1}{2T}= \frac{f_1 +f_2 } | :$$f_{\rm Nyq}= \frac{1}{2T}= \frac{f_1 +f_2 } | ||
{2 }\hspace{0.05cm}.$$ | {2 }\hspace{0.05cm}.$$ | ||
| − | * | + | *The '''rolloff factor''' is a measure of the transition steepness: |
:$$r = \frac{f_2 -f_1 } | :$$r = \frac{f_2 -f_1 } | ||
{f_2 +f_1 } \hspace{0.05cm}.$$ | {f_2 +f_1 } \hspace{0.05cm}.$$ | ||
| − | |||
| − | + | Notes: | |
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems|"Properties of Nyquist Systems"]]. | ||
| + | |||
| + | *The inverse Fourier transform $g(t)$ of a trapezoidal Nyquist spectrum with rolloff factor $r$ can be assumed to be known: | ||
| + | :$$g ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( { r \cdot | ||
| + | t}/{T}\right),\hspace{0.3cm} {\rm sinc}(x)= \sin(\pi \cdot x)/(\pi \cdot x).$$ | ||
| − | + | *A triangular low–pass spectrum $G(f)$ limited to $| f | < f_{0}$ and where $G(f = 0) = B$, after inverse Fourier transform, leads to the time function | |
| − | :$$g ( t )= B \cdot f_0 \cdot {\rm | + | :$$g ( t )= B \cdot f_0 \cdot {\rm sinc}^2 \left ( { f_0 \cdot t}\right)\hspace{0.05cm},\hspace{0.3cm} {\rm sinc}(x)= \sin(\pi \cdot x)/(\pi \cdot x).$$ |
| − | t}\right)\hspace{0.05cm}.$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {For the first questions, let $B = 0$. What is the Nyquist frequency? | ||
| + | |type="{}"} | ||
| + | $f_{\rm Nyq} \ = \ $ { 5 3% } $\ \rm kHz$ | ||
| + | |||
| + | {Which rolloff factor $r$ is present here? | ||
| + | |type="{}"} | ||
| + | $r \ = \ $ { 0.4 3% } | ||
| + | |||
| + | {Calculate the maximum value $g_{0}$ of the Nyquist pulse $g(t)$. | ||
| + | |type="{}"} | ||
| + | $g_{0} \ = \ ${ 1 3% } $\ \rm V$ | ||
| + | |||
| + | {Further let $B=0$. Calculate $g(t)$ for the time points $t = 100\, µ \rm s$ and $t = 200\, µ \rm s$. | ||
| + | |type="{}"} | ||
| + | $g(t = 100\, µ \rm s) \ = \ $ { 0. } $\ \rm V$ | ||
| + | $g(t = 200\, µ \rm s) \ = \ $ { 0. } $\ \rm V$ | ||
| + | |||
| + | {Calculate the pulse value at time $t = 250\ µ \rm s$. | ||
| + | |type="{}"} | ||
| + | $g(t = 250\, µ \rm s) \ = \ $ { 0. } $\ \rm V$ | ||
| + | |||
| + | {Which statements are true for $B \neq 0$? $G(f)$ is then complex-valued. | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | +The Nyquist condition is satisfied if the triangle function is between $3 \, \rm kHz$ and $7 \, \rm kHz$ as in the diagram. |
| − | + | + | - The Nyquist condition is fulfilled if the triangle function lies symmetrically between $3 \, \rm kHz$ and $5 \, \rm kHz$. |
| + | + The Nyquist condition is fulfilled if the triangle function lies symmetrically between $4.5 \, \rm kHz$ and $5.5 \, \rm kHz$. | ||
| − | { | + | {Calculate $g(t)$ for $t = 250\, µ \rm s$ and $B = A = 10^{–4} \, \rm V/Hz$ ⇒ complex spectral function. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $g(t = 250\ µ \rm s) \ = \ $ { 0.162 3% } $\ \rm V$ |
| Line 54: | Line 83: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The Nyquist frequency specifies the symmetry point of the rolloff. The following holds true: |
| − | '''(2)''' | + | :$$f_{\rm Nyq}= \frac{f_1 +f_2 } |
| − | '''(3)''' | + | {2 }= \frac{3\, {\rm kHz} + 7\, {\rm kHz}} {2 } \hspace{0.1cm}\underline { = 5\, {\rm kHz}} |
| − | '''(4)''' | + | \hspace{0.05cm}.$$ |
| − | '''(5)''' | + | |
| − | '''(6)''' | + | '''(2)''' The rolloff factor is also determined by the two corner frequencies $f_{1}$ and $f_{2}$: |
| + | :$$r = \frac{f_2 -f_1 } | ||
| + | {f_2 +f_1 } = \frac{7\, {\rm kHz} - 3\, {\rm kHz}} {7\, {\rm kHz} | ||
| + | + 3\, {\rm kHz} }\hspace{0.1cm}\underline { = 0.4 }\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(3)''' For a pulse with real low–pass spectrum, the maximum is always at $t = 0$ and it holds: | ||
| + | :$$g_0 = g(t=0) = \int_{-\infty}^{+\infty}G(f) \,{\rm d} f | ||
| + | = A \cdot 2 f_{\rm Nyq} = 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 5 \cdot10^{3} \,{\rm | ||
| + | Hz}\hspace{0.1cm}\underline { = 1\,{\rm V}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(4)''' For the Nyquist pulse, the equidistant zero crossings occur at the interval $T = 1/(2f_{\rm Nyq}) = 100 \, \rm µ s$. From this one obtains directly: | ||
| + | :$$g(t= 100\,{\rm µ s}) = \ \hspace{0.1cm}\underline { g(T) = 0,}$$ | ||
| + | :$$g(t= 200\,{\rm µ s}) = \ \hspace{0.1cm}\underline {g(2T) = 0} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | This result also follows from the given equation with $r = 0.4$: | ||
| + | :$$g ( t )= g_0 \cdot {\rm sinc} \left ( { | ||
| + | t}/{T}\right)\cdot {\rm sinc} \left ( {0.4 \cdot | ||
| + | t}/{T}\right) \hspace{0.05cm}.$$ | ||
| + | Responsible for satisfying the first Nyquist condition is the first term. | ||
| + | |||
| + | |||
| + | '''(5)''' According to the equation given in '''(4)''': | ||
| + | :$$g(t= 250\,{\rm µ s})= g_0 \cdot {\rm sinc} ( {1 })\cdot {\rm sinc} ( 2.5 )\hspace{0.1cm}\underline { = 0} \hspace{0.05cm}.$$ | ||
| + | This zero is due to the second term and does not lie in the Nyquist time grid $\nu T$ | ||
| + | |||
| + | |||
| + | '''(6)''' For the following derivation, let $g(t)= g_{\rm R}(t) + g_{\rm I}(t) \hspace{0.05cm},$ where $g_{\rm R}(t)$ is due to the real part and $g_{\rm I}(t)$ is due to the imaginary part of $G(f)$. | ||
| + | *The first part is calculated exactly as in point '''(4)''': | ||
| + | :$$g_{\rm R} ( t )= g_0 \cdot {\rm sinc} \left ( { | ||
| + | t}/{T}\right)\cdot {\rm sinc} \left ( { 0.4 \cdot | ||
| + | t}/{T}\right) \hspace{0.05cm}.$$ | ||
| + | *To satisfy the first Nyquist criterion, the following must hold for the imaginary part with $1/T = 10 \, \rm kHz$: | ||
| + | :$$\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G \left ( f - | ||
| + | {k}/{T} \right)\right]= 0 \hspace{0.05cm}.$$ | ||
| + | *With the given corner frequencies $f_{1} = 3 \, \rm kHz$ and $f_{2} = 7 \ \rm kHz$, the two triangles are around $\pm 5\, \rm kHz$, so the above equation is satisfied. | ||
| + | |||
| + | *The same is true for $f_{1} = 4.5\, \rm kHz$ and $f_{2} = 5.5 \, \rm kHz$. | ||
| + | |||
| + | *In contrast, the triangle peaks with $f_{1} = 3\, \rm kHz$ and $f_{2} = 5 \, \rm kHz$ are at $\pm 4 \ \rm kHz$. | ||
| + | |||
| + | *In this case the triangle functions do not cancel due to the periodic continuation and the Nyquist condition is not fulfilled. | ||
| + | |||
| + | |||
| + | Therefore the correct solutions are <u>1 and 3</u>. | ||
| + | |||
| + | |||
| + | '''(7)''' With the result $g_{\rm R}(2.5T) = 0$ from '''(3)''', it follows $g(2.5T) = g_{\rm I}(2.5T)$, where $g_{\rm I}(t)$ is the inverse Fourier transform of ${\rm j}\cdot \ G_{\rm I}(f)$. It holds: | ||
| + | :$${\rm j} \cdot G_{\rm I}(f) = {\rm j} \cdot\left[ \delta(f + f_{\rm Nyq}) - \delta(f - f_{\rm Nyq})\right] \star D(f) \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} g_{\rm I}(t) = 2 \cdot {\rm sin} ( 2 | ||
| + | \pi\cdot f_{\rm Nyq} \cdot t )\cdot d(t)\hspace{0.05cm}.$$ | ||
| + | *The sine function enforces the required zero crossings at multiples of $T = 100 \, \rm µ s$. | ||
| + | |||
| + | *$D(f)$ is a triangular function around $f = 0$ with $D(f = 0) = B$ and one-sided width $f_{0}= f_{2} - f_{\rm Nyq} = f_{\rm Nyq} - f_{1} = 2 \, \rm kHz$. | ||
| + | |||
| + | *For the associated time function we can thus write according to the specification: | ||
| + | :$$g_{\rm I}(t ) = 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2 | ||
| + | \pi\cdot f_{\rm Nyq} \cdot t)\cdot {\rm sinc}^2( f_{\rm 0} \cdot t) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *In particular, for time $t = 250 \, \rm µ s$ (green square): | ||
| + | :$$g(t = 2.5 T) = g_{\rm I}(t = 2.5 T) = \ 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2.5 | ||
| + | \pi )\cdot {\rm sinc}^2(0.5)= \ \frac{8}{\pi^2} \cdot B \cdot f_0 = \ \frac{8}{\pi^2} \cdot 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 10^{3} \,{\rm | ||
| + | Hz}\hspace{0.1cm}\underline {= 0.162\,{\rm | ||
| + | V}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | [[File:P_ID1283__Dig_Z_1_4g.png|right|frame|Asymmetric Nyquist pulse $g(t)= g_{\rm R}(t) + g_{\rm I}(t) $]] | ||
| + | The diagram shows the change of the time function due to the imaginary part (green time course): | ||
| + | *The result is now an asymmetric function curve $g(t)$, shown in blue. | ||
| + | *However, the zero crossings of $g_{\rm R}(t)$ at the distance $T$ remain. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 67: | Line 164: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^1.3 Nyquist System Properties^]] |
Latest revision as of 17:31, 1 May 2022
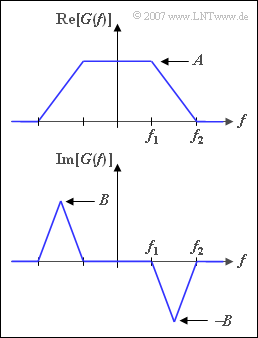
Consider a pulse $g(t)$ with spectrum $G(f)$ according to the sketch. One recognizes from this representation:
- The real part of $G(f)$ is trapezoidal with the corner frequencies $f_{1} = 3 \, \rm kHz$ and $f_{2} = 7 \, \rm kHz$. In the range $|f| < f_{1}$:
- $${\rm Re}\big[G(f)\big] = A = 10^{-4} \, \rm V/Hz.$$
- The imaginary part of $G(f)$ is always assumed to be ${\rm Im}\big[G(f)\big] =0$ for subtasks (1) to (5). In this case $g(t)$ is certainly a Nyquist pulse.
- From subtask (6), the imaginary part ${\rm Im}[G(f)]$ in the range $f_{1} \leq | f | \leq f_{2}$ has a triangular shape with the values $\pm B$ at the triangle peaks.
It is necessary to check whether the pulse $g(t)$ satisfies the first Nyquist condition even with complex spectrum:
- $$g(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$$
In the course of this exercise, reference is made to the following descriptive quantities:
- The Nyquist frequency gives the symmetry point of the rolloff:
- $$f_{\rm Nyq}= \frac{1}{2T}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- The rolloff factor is a measure of the transition steepness:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Properties of Nyquist Systems".
- The inverse Fourier transform $g(t)$ of a trapezoidal Nyquist spectrum with rolloff factor $r$ can be assumed to be known:
- $$g ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( { r \cdot t}/{T}\right),\hspace{0.3cm} {\rm sinc}(x)= \sin(\pi \cdot x)/(\pi \cdot x).$$
- A triangular low–pass spectrum $G(f)$ limited to $| f | < f_{0}$ and where $G(f = 0) = B$, after inverse Fourier transform, leads to the time function
- $$g ( t )= B \cdot f_0 \cdot {\rm sinc}^2 \left ( { f_0 \cdot t}\right)\hspace{0.05cm},\hspace{0.3cm} {\rm sinc}(x)= \sin(\pi \cdot x)/(\pi \cdot x).$$
Questions
Solution
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }= \frac{3\, {\rm kHz} + 7\, {\rm kHz}} {2 } \hspace{0.1cm}\underline { = 5\, {\rm kHz}} \hspace{0.05cm}.$$
(2) The rolloff factor is also determined by the two corner frequencies $f_{1}$ and $f_{2}$:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } = \frac{7\, {\rm kHz} - 3\, {\rm kHz}} {7\, {\rm kHz} + 3\, {\rm kHz} }\hspace{0.1cm}\underline { = 0.4 }\hspace{0.05cm}.$$
(3) For a pulse with real low–pass spectrum, the maximum is always at $t = 0$ and it holds:
- $$g_0 = g(t=0) = \int_{-\infty}^{+\infty}G(f) \,{\rm d} f = A \cdot 2 f_{\rm Nyq} = 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 5 \cdot10^{3} \,{\rm Hz}\hspace{0.1cm}\underline { = 1\,{\rm V}}\hspace{0.05cm}.$$
(4) For the Nyquist pulse, the equidistant zero crossings occur at the interval $T = 1/(2f_{\rm Nyq}) = 100 \, \rm µ s$. From this one obtains directly:
- $$g(t= 100\,{\rm µ s}) = \ \hspace{0.1cm}\underline { g(T) = 0,}$$
- $$g(t= 200\,{\rm µ s}) = \ \hspace{0.1cm}\underline {g(2T) = 0} \hspace{0.05cm}.$$
This result also follows from the given equation with $r = 0.4$:
- $$g ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( {0.4 \cdot t}/{T}\right) \hspace{0.05cm}.$$
Responsible for satisfying the first Nyquist condition is the first term.
(5) According to the equation given in (4):
- $$g(t= 250\,{\rm µ s})= g_0 \cdot {\rm sinc} ( {1 })\cdot {\rm sinc} ( 2.5 )\hspace{0.1cm}\underline { = 0} \hspace{0.05cm}.$$
This zero is due to the second term and does not lie in the Nyquist time grid $\nu T$
(6) For the following derivation, let $g(t)= g_{\rm R}(t) + g_{\rm I}(t) \hspace{0.05cm},$ where $g_{\rm R}(t)$ is due to the real part and $g_{\rm I}(t)$ is due to the imaginary part of $G(f)$.
- The first part is calculated exactly as in point (4):
- $$g_{\rm R} ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( { 0.4 \cdot t}/{T}\right) \hspace{0.05cm}.$$
- To satisfy the first Nyquist criterion, the following must hold for the imaginary part with $1/T = 10 \, \rm kHz$:
- $$\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G \left ( f - {k}/{T} \right)\right]= 0 \hspace{0.05cm}.$$
- With the given corner frequencies $f_{1} = 3 \, \rm kHz$ and $f_{2} = 7 \ \rm kHz$, the two triangles are around $\pm 5\, \rm kHz$, so the above equation is satisfied.
- The same is true for $f_{1} = 4.5\, \rm kHz$ and $f_{2} = 5.5 \, \rm kHz$.
- In contrast, the triangle peaks with $f_{1} = 3\, \rm kHz$ and $f_{2} = 5 \, \rm kHz$ are at $\pm 4 \ \rm kHz$.
- In this case the triangle functions do not cancel due to the periodic continuation and the Nyquist condition is not fulfilled.
Therefore the correct solutions are 1 and 3.
(7) With the result $g_{\rm R}(2.5T) = 0$ from (3), it follows $g(2.5T) = g_{\rm I}(2.5T)$, where $g_{\rm I}(t)$ is the inverse Fourier transform of ${\rm j}\cdot \ G_{\rm I}(f)$. It holds:
- $${\rm j} \cdot G_{\rm I}(f) = {\rm j} \cdot\left[ \delta(f + f_{\rm Nyq}) - \delta(f - f_{\rm Nyq})\right] \star D(f) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_{\rm I}(t) = 2 \cdot {\rm sin} ( 2 \pi\cdot f_{\rm Nyq} \cdot t )\cdot d(t)\hspace{0.05cm}.$$
- The sine function enforces the required zero crossings at multiples of $T = 100 \, \rm µ s$.
- $D(f)$ is a triangular function around $f = 0$ with $D(f = 0) = B$ and one-sided width $f_{0}= f_{2} - f_{\rm Nyq} = f_{\rm Nyq} - f_{1} = 2 \, \rm kHz$.
- For the associated time function we can thus write according to the specification:
- $$g_{\rm I}(t ) = 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2 \pi\cdot f_{\rm Nyq} \cdot t)\cdot {\rm sinc}^2( f_{\rm 0} \cdot t) \hspace{0.05cm}.$$
- In particular, for time $t = 250 \, \rm µ s$ (green square):
- $$g(t = 2.5 T) = g_{\rm I}(t = 2.5 T) = \ 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2.5 \pi )\cdot {\rm sinc}^2(0.5)= \ \frac{8}{\pi^2} \cdot B \cdot f_0 = \ \frac{8}{\pi^2} \cdot 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 10^{3} \,{\rm Hz}\hspace{0.1cm}\underline {= 0.162\,{\rm V}} \hspace{0.05cm}.$$
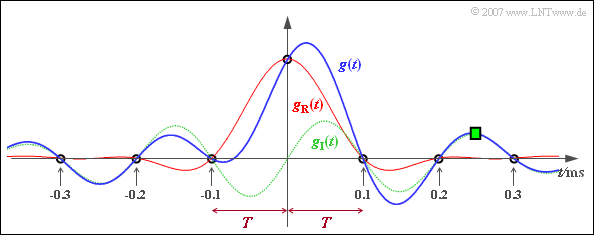
The diagram shows the change of the time function due to the imaginary part (green time course):
- The result is now an asymmetric function curve $g(t)$, shown in blue.
- However, the zero crossings of $g_{\rm R}(t)$ at the distance $T$ remain.