Difference between revisions of "Aufgaben:Exercise 1.08Z: BPSK Error Probability"
m (Text replacement - "Category:Aufgaben zu Digitalsignalübertragung" to "Category:Digital Signal Transmission: Exercises") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation |
}} | }} | ||
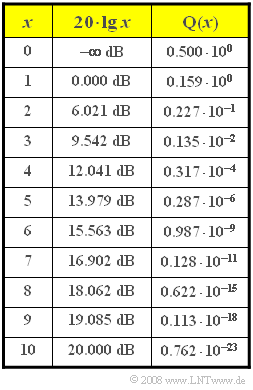
| − | [[File:P_ID1681__Dig_Z_4_1.png|right|frame| | + | [[File:P_ID1681__Dig_Z_4_1.png|right|frame|Numerical values of function ${\rm Q}(x)$]] |
| − | + | We assume the optimal baseband transmission system for binary signals with | |
| − | * | + | *bipolar amplitude coefficients $a_{\nu} \in \{–1, +1\}$, |
| − | |||
| − | |||
| − | |||
| − | |||
| + | *rectangular transmitted signal with signal values $\pm s_{0}$ and bit duration $T_{\rm B}$, | ||
| − | + | *AWGN noise with noise power density $N_{0}$, | |
| − | |||
| − | + | *receiver filter according to the matched filter principle, | |
| − | |||
| − | + | *decision with the optimal threshold $E = 0$. | |
| − | |||
| − | |||
| − | |||
| − | + | Unless otherwise specified, you should also assume the following numerical values: | |
| − | :$$ | + | :$$ s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$ |
| + | The bit error probability of this "baseband system" has already been given in the chapter [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission|"Error Probability for Baseband Transmission"]] $($Index: $\rm BB)$: | ||
| + | :$$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$ | ||
| + | Here, $\sigma_{d}$ denotes the noise rms value at the decision device and ${\rm Q}(x)$ denotes the complementary Gaussian error function, which is given here in tabular form. This error probability can also be expressed in the form | ||
| + | :$$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$ | ||
| + | where $E_{\rm B}$ denotes "energy per bit." | ||
| + | The error probability of a comparable transmission system with "Binary Phase Shift Keying" is $($Index: $\rm BPSK)$: | ||
| + | :$$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$ | ||
| − | + | ||
| − | * | + | Notes: |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]]. |
| + | |||
| + | *Reference is also made to the chapter [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission|"Error Probability for Baseband Transmission"]]. | ||
| − | * | + | *You can check the results with the HTML5/JavaScript applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Complementary Gaussian Error Functions"]]. |
| − | * | + | |
| + | *Since the signal value $s_{0}$ is specified here in "volts" and no specification is made for the reference resistance, $E_{\rm B}$ has the unit "$\rm V^{2}/Hz$". | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Let $s_{0} = 4 \, \rm V$. What is the error probability $p_{\rm BB}$ of the baseband system? |
|type="{}"} | |type="{}"} | ||
$p_{\rm BB} \ = \ $ { 0.00317 3% } $\ \% $ | $p_{\rm BB} \ = \ $ { 0.00317 3% } $\ \% $ | ||
| − | { | + | {What is the energy per bit for the baseband system with $s_{0} = 4 \, \rm V$? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 1.6 3% } $\ \cdot 10^{-8}\ \rm V^{2}s $ | $E_{\rm B} \ = \ $ { 1.6 3% } $\ \cdot 10^{-8}\ \rm V^{2}s $ | ||
| − | { | + | {What is the error probability $p_{\rm BB}$ at half the transmission amplitude $(s_{0} = 2 \, \rm V)$? |
|type="{}"} | |type="{}"} | ||
$p_{\rm BB} \ = \ $ { 2.27 3% } $\ \% $ | $p_{\rm BB} \ = \ $ { 2.27 3% } $\ \% $ | ||
| − | { | + | {Give the error probability of the BPSK depending on the quotient $E_{\rm B}/N_{0}$. Which result is correct? |
|type="[]"} | |type="[]"} | ||
- $p_{\rm BPSK} = {\rm Q}\big [(E_{\rm B}/N_{0})^{1/2}\big ]$, | - $p_{\rm BPSK} = {\rm Q}\big [(E_{\rm B}/N_{0})^{1/2}\big ]$, | ||
| Line 64: | Line 66: | ||
-$p_{\rm BPSK} = {\rm Q}\big [(4\cdot E_{\rm B}/N_{0})^{1/2}\big ]$. | -$p_{\rm BPSK} = {\rm Q}\big [(4\cdot E_{\rm B}/N_{0})^{1/2}\big ]$. | ||
| − | { | + | {What are the error probabilities for the BPSK and $E_{\rm B}/N_{0} = 8$ resp. $E_{\rm B}/N_{0} = 2$? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B}/N_{0} = 8\text{:}\hspace{0.4cm} p_{\rm BPSK} \ = \ $ { 0.00317 3% } $\ \% $ | $E_{\rm B}/N_{0} = 8\text{:}\hspace{0.4cm} p_{\rm BPSK} \ = \ $ { 0.00317 3% } $\ \% $ | ||
| Line 73: | Line 75: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The noise rms value is given here by |
:$$\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}= \sqrt{\frac{2 \cdot 10^{-9}\,{\rm V^2/Hz}}{2 \cdot 1\,{\rm ns}}}= 1\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm BB} = {\rm Q}\left ({s_0}/{\sigma_d } \right | :$$\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}= \sqrt{\frac{2 \cdot 10^{-9}\,{\rm V^2/Hz}}{2 \cdot 1\,{\rm ns}}}= 1\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm BB} = {\rm Q}\left ({s_0}/{\sigma_d } \right | ||
)= {\rm Q}(4)= 0.317 \cdot 10^{-4}\hspace{0.1cm}\underline {= 0.00317 \%}.$$ | )= {\rm Q}(4)= 0.317 \cdot 10^{-4}\hspace{0.1cm}\underline {= 0.00317 \%}.$$ | ||
| − | '''(2)''' | + | '''(2)''' For the baseband system: |
:$$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot | :$$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot | ||
10^{-9}\,{\rm s}\hspace{0.1cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$ | 10^{-9}\,{\rm s}\hspace{0.1cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$ | ||
| − | + | *Of course, the additional given equation gives the exact same error probability: | |
:$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right | :$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right | ||
) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm | ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm | ||
| Line 89: | Line 91: | ||
) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$ | ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$ | ||
| − | + | *A comparison with question '''(4)''' of [[Aufgaben:Exercise_1.08:_Comparison_of_ASK_and_BPSK|"Exercise 1.8"]] shows that $E_{\rm B}/N_{0} = 8$ is not (exactly) equal to $10 \cdot \lg E_{\rm B}/N_{0} = 9 \ \rm dB$. | |
| + | *In the first case $p_{\rm BB} = 0.317 \cdot 10^{–4}$ is obtained, in the second $p_{\rm BB} = 0.336 \cdot 10^{-4}$. | ||
| − | '''(3)''' | + | '''(3)''' At half the transmission amplitude $s_{0} = 2 \ \rm V$, the energy per bit decreases to a quarter and the following equations apply: |
:$$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )\hspace{0.1cm}\underline {= {\rm Q}(2)= 2.27 \%},$$ | :$$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )\hspace{0.1cm}\underline {= {\rm Q}(2)= 2.27 \%},$$ | ||
:$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)= 2.27 \%.$$ | :$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)= 2.27 \%.$$ | ||
| − | '''(4)''' | + | '''(4)''' Considering only half the energy $E_{\rm B} = s^{2}_{0} \cdot T_{\rm B}/2$, we obtain with $\sigma^{2}_{d} = N_{0}/T_{\rm B}$ and |
:$$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )= {\rm Q}\left ( \sqrt{{s_0^2 \cdot T_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }}\hspace{0.1cm}\right )$$ | :$$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )= {\rm Q}\left ( \sqrt{{s_0^2 \cdot T_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }}\hspace{0.1cm}\right )$$ | ||
| − | + | the exact same result as for the optimal baseband system ⇒ <u>solution 2</u>. | |
| − | '''(5)''' | + | '''(5)''' Of course, this also gives the exact same results as for the baseband transmission: |
:$${ E_{\rm B}}/{N_0 }= 8{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{16}) = {\rm Q}(4)\hspace{0.1cm}\underline {= 0.00317 \%},$$ | :$${ E_{\rm B}}/{N_0 }= 8{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{16}) = {\rm Q}(4)\hspace{0.1cm}\underline {= 0.00317 \%},$$ | ||
:$${ E_{\rm B}}/{N_0 }= 2{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{4}) = {\rm Q}(2) \hspace{0.1cm}\underline {= 2.27 \%}.$$ | :$${ E_{\rm B}}/{N_0 }= 2{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{4}) = {\rm Q}(2) \hspace{0.1cm}\underline {= 2.27 \%}.$$ | ||
| Line 111: | Line 114: | ||
| − | [[Category:Digital Signal Transmission: Exercises|^1.5 | + | [[Category:Digital Signal Transmission: Exercises|^1.5 Linear Digital Modulation^]] |
Latest revision as of 16:12, 10 May 2022
We assume the optimal baseband transmission system for binary signals with
- bipolar amplitude coefficients $a_{\nu} \in \{–1, +1\}$,
- rectangular transmitted signal with signal values $\pm s_{0}$ and bit duration $T_{\rm B}$,
- AWGN noise with noise power density $N_{0}$,
- receiver filter according to the matched filter principle,
- decision with the optimal threshold $E = 0$.
Unless otherwise specified, you should also assume the following numerical values:
- $$ s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$
The bit error probability of this "baseband system" has already been given in the chapter "Error Probability for Baseband Transmission" $($Index: $\rm BB)$:
- $$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$
Here, $\sigma_{d}$ denotes the noise rms value at the decision device and ${\rm Q}(x)$ denotes the complementary Gaussian error function, which is given here in tabular form. This error probability can also be expressed in the form
- $$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$
where $E_{\rm B}$ denotes "energy per bit."
The error probability of a comparable transmission system with "Binary Phase Shift Keying" is $($Index: $\rm BPSK)$:
- $$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".
- Reference is also made to the chapter "Error Probability for Baseband Transmission".
- You can check the results with the HTML5/JavaScript applet "Complementary Gaussian Error Functions".
- Since the signal value $s_{0}$ is specified here in "volts" and no specification is made for the reference resistance, $E_{\rm B}$ has the unit "$\rm V^{2}/Hz$".
Questions
Solution
- $$\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}= \sqrt{\frac{2 \cdot 10^{-9}\,{\rm V^2/Hz}}{2 \cdot 1\,{\rm ns}}}= 1\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm BB} = {\rm Q}\left ({s_0}/{\sigma_d } \right )= {\rm Q}(4)= 0.317 \cdot 10^{-4}\hspace{0.1cm}\underline {= 0.00317 \%}.$$
(2) For the baseband system:
- $$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot 10^{-9}\,{\rm s}\hspace{0.1cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$
- Of course, the additional given equation gives the exact same error probability:
- $$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$
- A comparison with question (4) of "Exercise 1.8" shows that $E_{\rm B}/N_{0} = 8$ is not (exactly) equal to $10 \cdot \lg E_{\rm B}/N_{0} = 9 \ \rm dB$.
- In the first case $p_{\rm BB} = 0.317 \cdot 10^{–4}$ is obtained, in the second $p_{\rm BB} = 0.336 \cdot 10^{-4}$.
(3) At half the transmission amplitude $s_{0} = 2 \ \rm V$, the energy per bit decreases to a quarter and the following equations apply:
- $$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )\hspace{0.1cm}\underline {= {\rm Q}(2)= 2.27 \%},$$
- $$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)= 2.27 \%.$$
(4) Considering only half the energy $E_{\rm B} = s^{2}_{0} \cdot T_{\rm B}/2$, we obtain with $\sigma^{2}_{d} = N_{0}/T_{\rm B}$ and
- $$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )= {\rm Q}\left ( \sqrt{{s_0^2 \cdot T_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }}\hspace{0.1cm}\right )$$
the exact same result as for the optimal baseband system ⇒ solution 2.
(5) Of course, this also gives the exact same results as for the baseband transmission:
- $${ E_{\rm B}}/{N_0 }= 8{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{16}) = {\rm Q}(4)\hspace{0.1cm}\underline {= 0.00317 \%},$$
- $${ E_{\rm B}}/{N_0 }= 2{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{4}) = {\rm Q}(2) \hspace{0.1cm}\underline {= 2.27 \%}.$$