Difference between revisions of "Aufgaben:Exercise 2.1: ACF and PSD with Coding"
| (21 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Basics_of_Coded_Transmission |
}} | }} | ||
| − | [[File:P_ID1308__Dig_A_2_1.png|right|frame| | + | [[File:P_ID1308__Dig_A_2_1.png|right|frame|Power-spectral density with coding]] |
| − | + | We consider the digital signal $s(t)$, using the following descriptive quantities: | |
| − | + | *$a_{\nu}$ are the amplitude coefficients, | |
| − | + | *$g_{s}(t)$ indicates the basic transmission pulse, | |
| − | *$a_{\nu}$ | + | *$T$ is the symbol duration (spacing of the pulses). |
| − | *$g_{s}(t)$ | ||
| − | *$T$ | ||
| − | + | Then holds: | |
| − | * | + | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$ |
| + | |||
| + | To characterize the spectral properties resulting from the coding and pulse shaping, one uses, among other things | ||
| + | *the auto-correlation function $\rm (ACF)$ | ||
:$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm},$$ | :$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm},$$ | ||
| − | * | + | *the power-spectral density $\rm (PSD)$ |
:$${\it \Phi}_s(f) = {1}/{T} \cdot {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \hspace{0.05cm}.$$ | :$${\it \Phi}_s(f) = {1}/{T} \cdot {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \hspace{0.05cm}.$$ | ||
| − | + | Here, $\varphi_{a}(\lambda)$ denotes the discrete ACF of the amplitude coefficients related to the power-spectral density ${\it \Phi}_{a}(f)$ via the Fourier transform. Thus, for this holds: | |
:$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$ | :$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$ | ||
| − | + | Furthermore, the energy ACF and energy spectrum are used in above equations: | |
:$$\varphi^{^{\bullet}}_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm}.$$ | :$$\varphi^{^{\bullet}}_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm}.$$ | ||
| − | In | + | |
| + | |||
| + | In the present exercise, the following function is to be assumed for the power-spectral density of the amplitude coefficients (see graph): | ||
:$${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$ | :$${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$ | ||
| − | + | The following assumptions are made for the basic transmission pulse: | |
| − | * | + | *In question '''(2)''', let $g_{s}(t)$ be an NRZ rectangular pulse, so that there is a triangular energy ACF confined to the range $|\tau| ≤ T$. The maximum value here is |
:$$\varphi^{^{\bullet}}_{gs}(\tau = 0) = s_0^2 \cdot T \hspace{0.05cm}.$$ | :$$\varphi^{^{\bullet}}_{gs}(\tau = 0) = s_0^2 \cdot T \hspace{0.05cm}.$$ | ||
| − | * | + | *For question '''(3)''', assume a root-Nyquist characteristic with rolloff factor $r = 0$. In this case holds: |
| − | :$$|G_s(f)|^2 = \left\{ \begin{array}{c} s_0^2 \cdot T^2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{ | + | :$$|G_s(f)|^2 = \left\{ \begin{array}{c} s_0^2 \cdot T^2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c} |f| < {1}/({2T}) \hspace{0.05cm}, \\ |f| > {1}/({2T}) \hspace{0.05cm}.\\ \end{array}$$ |
| − | * | + | *For numerical calculations, use always $s_{0}^{2} = 10 \ \rm mW$. |
| − | |||
| − | |||
| − | === | + | Notes: |
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Basics_of_Coded_Transmission|"Basics of Coded Transmission"]]. | ||
| + | |||
| + | *Consider that the transmit power $P_{\rm S}$ is equal to the ACF $\varphi_{s}(\tau)$ at the point $\tau = 0$, but can also be calculated as an integral over the PSD ${\it \Phi}_{s}(f)$. | ||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {What are the discrete ACF values $\varphi_{a}(\lambda)$ of the amplitude coefficients? Enter the numerical values for $\lambda = 0$, $\lambda = 1$ and $\lambda = 2$. | ||
| + | |type="{}"} | ||
| + | $\varphi_{a}(\lambda = 0) \ = \ $ { 0.5 3% } | ||
| + | $\varphi_{a}(\lambda = 1) \ = \ $ { 0. } | ||
| + | $\varphi_{a}(\lambda = 2) \ = \ $ { -0.2575--0.2425 } | ||
| + | |||
| + | {What is the transmit power with the <u>NRZ basic transmission pulse</u>? | ||
| + | |type="{}"} | ||
| + | $P_{\rm S} \ = \ $ { 5 3% } $ \ \rm mW$ | ||
| − | { | + | {What is the transmit power with <u>root-Nyquist characteristic</u> $(r = 0)$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $P_{\rm S} \ = \ $ { 5 3% } $ \ \rm mW$ |
| Line 56: | Line 67: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
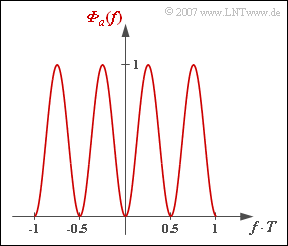
| − | '''(1)''' | + | '''(1)''' Since ${\it \Phi}_{a}(f)$ as a power-spectral density is always real (plus even and positive, but that does not matter here) and the ACF values $\varphi_{a}(\lambda)$ are symmetric about $\lambda = 0$, the given equation can be transformed as follows: |
| − | '''(2)''' | + | :$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(0) + \sum_{\lambda = 1}^{\infty}2 \cdot \varphi_a(\lambda)\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) \hspace{0.05cm}.$$ |
| − | '''(3)''' | + | *By comparison with the sketched function |
| − | + | :$${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$ | |
| − | + | :one obtains: | |
| − | + | :$${\it \varphi}_a(\lambda = 0)\hspace{0.15cm}\underline { = 0.5}, \hspace{0.2cm} {\it \varphi}_a(\lambda = 2) = {\it \varphi}_a(\lambda = -2) \hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm}.$$ | |
| + | *All other ACF values result to zero, so also $\varphi_{a}(\lambda = ±1)\hspace{0.15cm}\underline {=0}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' For the rectangular NRZ basic pulse, due to the limitation of the energy ACF to the range $|\tau| ≤ T$, we obtain: | ||
| + | :$$P_{\rm S} = \varphi_s(\tau = 0) = \frac{1}{T} \cdot \varphi_a(\lambda = 0)\cdot \varphi^{^{\bullet}}_{gs}(\tau = 0)= \frac{1}{T} \cdot \frac{1}{2} \cdot s_0^2 \cdot T = \frac{s_0^2}{2} \hspace{0.15cm}\underline {= 5\,\,{\rm mW}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' For rectangular spectral function, it is more convenient to calculate the transmit power by integration over the power-spectral density: | ||
| + | :$$P_{\rm S} = \ \int_{-1/(2T)}^{+1/(2T)} {\it \Phi}_s(f) \,{\rm d} f = \frac{1}{T} \cdot \int_{-1/(2T)}^{+1/(2T)} {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \,{\rm d} f$$ | ||
| + | :$$\Rightarrow\hspace{0.3cm}P_{\rm S} = \ \frac{1}{T} \cdot \left [ s_0^2 \cdot T^2 \right ] \cdot \int_{-1/(2T)}^{+1/(2T)} \left( {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\right ) \,{\rm d} f\hspace{0.05cm} = {s_0^2}/{2}\hspace{0.15cm}\underline { = 5\,\,{\rm mW}} .$$ | ||
| + | *Here it is considered that the energy PSD $|G_{s}(f)|^{2}$ is given as constant (within the integration interval) and thus can be drawn in front of the integral. | ||
| + | *In spite of a completely different signal form $s(t)$, the same transmit power results here, since the integral yields the value $1/(2T)$. | ||
| + | *It should be noted that this simple calculation is only possible for the rolloff factor $r = 0$. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 69: | Line 95: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.1 Basics of Coded Transmission^]] |
Latest revision as of 15:23, 23 May 2022
We consider the digital signal $s(t)$, using the following descriptive quantities:
- $a_{\nu}$ are the amplitude coefficients,
- $g_{s}(t)$ indicates the basic transmission pulse,
- $T$ is the symbol duration (spacing of the pulses).
Then holds:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$
To characterize the spectral properties resulting from the coding and pulse shaping, one uses, among other things
- the auto-correlation function $\rm (ACF)$
- $$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm},$$
- the power-spectral density $\rm (PSD)$
- $${\it \Phi}_s(f) = {1}/{T} \cdot {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \hspace{0.05cm}.$$
Here, $\varphi_{a}(\lambda)$ denotes the discrete ACF of the amplitude coefficients related to the power-spectral density ${\it \Phi}_{a}(f)$ via the Fourier transform. Thus, for this holds:
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$
Furthermore, the energy ACF and energy spectrum are used in above equations:
- $$\varphi^{^{\bullet}}_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm}.$$
In the present exercise, the following function is to be assumed for the power-spectral density of the amplitude coefficients (see graph):
- $${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$
The following assumptions are made for the basic transmission pulse:
- In question (2), let $g_{s}(t)$ be an NRZ rectangular pulse, so that there is a triangular energy ACF confined to the range $|\tau| ≤ T$. The maximum value here is
- $$\varphi^{^{\bullet}}_{gs}(\tau = 0) = s_0^2 \cdot T \hspace{0.05cm}.$$
- For question (3), assume a root-Nyquist characteristic with rolloff factor $r = 0$. In this case holds:
- $$|G_s(f)|^2 = \left\{ \begin{array}{c} s_0^2 \cdot T^2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c} |f| < {1}/({2T}) \hspace{0.05cm}, \\ |f| > {1}/({2T}) \hspace{0.05cm}.\\ \end{array}$$
- For numerical calculations, use always $s_{0}^{2} = 10 \ \rm mW$.
Notes:
- The exercise belongs to the chapter "Basics of Coded Transmission".
- Consider that the transmit power $P_{\rm S}$ is equal to the ACF $\varphi_{s}(\tau)$ at the point $\tau = 0$, but can also be calculated as an integral over the PSD ${\it \Phi}_{s}(f)$.
Questions
Solution
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(0) + \sum_{\lambda = 1}^{\infty}2 \cdot \varphi_a(\lambda)\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) \hspace{0.05cm}.$$
- By comparison with the sketched function
- $${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$
- one obtains:
- $${\it \varphi}_a(\lambda = 0)\hspace{0.15cm}\underline { = 0.5}, \hspace{0.2cm} {\it \varphi}_a(\lambda = 2) = {\it \varphi}_a(\lambda = -2) \hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm}.$$
- All other ACF values result to zero, so also $\varphi_{a}(\lambda = ±1)\hspace{0.15cm}\underline {=0}$.
(2) For the rectangular NRZ basic pulse, due to the limitation of the energy ACF to the range $|\tau| ≤ T$, we obtain:
- $$P_{\rm S} = \varphi_s(\tau = 0) = \frac{1}{T} \cdot \varphi_a(\lambda = 0)\cdot \varphi^{^{\bullet}}_{gs}(\tau = 0)= \frac{1}{T} \cdot \frac{1}{2} \cdot s_0^2 \cdot T = \frac{s_0^2}{2} \hspace{0.15cm}\underline {= 5\,\,{\rm mW}}\hspace{0.05cm}.$$
(3) For rectangular spectral function, it is more convenient to calculate the transmit power by integration over the power-spectral density:
- $$P_{\rm S} = \ \int_{-1/(2T)}^{+1/(2T)} {\it \Phi}_s(f) \,{\rm d} f = \frac{1}{T} \cdot \int_{-1/(2T)}^{+1/(2T)} {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \,{\rm d} f$$
- $$\Rightarrow\hspace{0.3cm}P_{\rm S} = \ \frac{1}{T} \cdot \left [ s_0^2 \cdot T^2 \right ] \cdot \int_{-1/(2T)}^{+1/(2T)} \left( {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\right ) \,{\rm d} f\hspace{0.05cm} = {s_0^2}/{2}\hspace{0.15cm}\underline { = 5\,\,{\rm mW}} .$$
- Here it is considered that the energy PSD $|G_{s}(f)|^{2}$ is given as constant (within the integration interval) and thus can be drawn in front of the integral.
- In spite of a completely different signal form $s(t)$, the same transmit power results here, since the integral yields the value $1/(2T)$.
- It should be noted that this simple calculation is only possible for the rolloff factor $r = 0$.