Difference between revisions of "Channel Coding/Examples of Binary Block Codes"
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Binary Block Codes for Channel Coding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Channel Models and Decision Structures |
| − | |Nächste Seite= | + | |Nächste Seite=General Description of Linear Block Codes |
}} | }} | ||
| − | == Single | + | == Single Parity Check Codes== |
<br> | <br> | ||
| − | + | The <i>Single Parity Check Code</i> (SPC) adds to the information block $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ a parity bit $p$ : | |
| − | [[File:P ID2346 KC T 1 3 S1 v2.png|right|frame| | + | [[File:P ID2346 KC T 1 3 S1 v2.png|right|frame|Various single parity check codes $(n = k + 1)$|class=fit]] |
:$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$ | :$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$ | ||
:$$\Rightarrow \hspace{0.3cm} | :$$\Rightarrow \hspace{0.3cm} | ||
| Line 15: | Line 15: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The graphic shows three coding examples: | |
*$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \ (k = 2)$, | *$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \ (k = 2)$, | ||
| Line 23: | Line 23: | ||
| − | + | This very simple code can be characterized as follows: | |
| − | * | + | *From $n = k + 1$ follows for the ''code rate'' $R = k/n = (n-1)/n$ and for the ''redundancy'' $1-R = 1/n$. For $k = 2$ , for example, the code rate is $2/3$ and the relative redundancy is $33.3\%$. |
| − | * | + | *The parity bit is obtained by modulo–2–addition. This is the addition in the [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois field|Galois field]] to the base $2$ ⇒ $\rm GF(2)$, so that $1 \oplus 1 = 0$ results: |
::<math>p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k | ::<math>p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Thus every valid codeword $\underline{x}$ contains an even number of ones. Expressed as $\oplus$ or in simplified notation according to the second equation, this condition reads: |
::<math> x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 | ::<math> x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 | ||
| − | \hspace{0.05cm}, \hspace{0.5cm}{\rm | + | \hspace{0.05cm}, \hspace{0.5cm}{\rm or:}\hspace{0.5cm} |
\sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} | \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} | ||
, \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} | , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} | ||
\hspace{0.05cm}. </math> | \hspace{0.05cm}. </math> | ||
| − | * | + | *For $k = 2$ ⇒ $n = 3$ the following four code words result, where the parity bit $p$ is marked by a small arrow in each case: |
::<math>\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} | ::<math>\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} | ||
\underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.</math> | \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.</math> | ||
| − | * | + | *This code $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$ is ''linear'' since the sum of any two codewords again gives a valid codeword, for example. |
:$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$ | :$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$ | ||
| − | * | + | *For any $k$ ⇒ $n = k+1$ each codeword differs from all others at an even number of positions. Thus, the minimum distance of the code is |
:$$d_{\rm min} = 2.$$ | :$$d_{\rm min} = 2.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Each $\text{Single Parity Check Code (SPC)}$ can be formally described as follows: |
| − | ::<math>\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm | + | ::<math>\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm with \hspace{0.15cm}even\hspace{0.15cm} number\hspace{0.15cm} of\hspace{0.15cm} ones\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.</math> |
| − | * | + | *With the general code name $(n, \ k, \ d_{\rm min})$ any <i>Single Parity–check Code</i> can also be named $\text{SPC }(n, \ n-1, \ 2)$ . |
| − | * | + | *The top graph thus shows the $\text{SPC (3, 2, 2)}$, the $\text{SPC (4, 3, 2)}$, and the $\text{SPC (5, 4, 2)}$.}}<br> |
| − | + | The digital channel may change the codeword $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$ to the receive word $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. With the error vector $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$ holds: | |
:$$\underline{y}= \underline{x} \oplus \underline{e}.$$ | :$$\underline{y}= \underline{x} \oplus \underline{e}.$$ | ||
| − | + | For decoding the <i>Single Parity Check Code</i> one forms the so-called '''syndrome''': | |
::<math>s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} | ::<math>s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | The result $s=1$ then indicates (at least) one bit error within the codeword, while $s=0$ should be interpreted as follows: | |
| − | * | + | *The transmission was error-free, or:<br> |
| − | * | + | *The number of bit errors is even.<br><br> |
| − | [[File:P ID2382 KC T 1 3 S1c.png|right|frame| | + | [[File:P ID2382 KC T 1 3 S1c.png|right|frame|Possible received values at the $\text{SPC (4, 3, 2)}$ |class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We consider the $\text{SPC (4, 3, 2)}$ and assume that the null word was sent. The table shows all possibilities that $f$ bits are corrupted and gives the respective syndrome $s \in \{0, 1\}$ . |
| − | + | For the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|BSC model]] with the crossover probability (Noah) $\varepsilon = 1\%$ the following probabilities then result: | |
| − | * | + | *The information word is correctly decoded (blue background): |
::<math>{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.</math> | ::<math>{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.</math> | ||
| − | * | + | *The decoder detects that transmission errors have occurred (green background): |
::<math>{\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.</math> | ::<math>{\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.</math> | ||
| − | * | + | *The information word is decoded incorrectly (red background): |
::<math>{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.</math> | ::<math>{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.</math> | ||
| − | + | We refer here to the interactive applet [[Applets:Binomial-_und_Poissonverteilung_(Applet)|Binomial and Poisson Distribution]]. The results obtained here are also discussed again in the [[Aufgaben:Exercise_1.5:_SPC_(5,_4)_and_BEC_Model|Exercise A1.5]] }}<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ Error correction of the single parity–check code is not possible for the BSC–model unlike the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|BEC–channel]] (<i>Binary Erasure Channel</i>). |
| − | + | Bit errors are excluded with this one. If only one bit is erased $($ <i>erasure</i>, $\rm E)$, then due to the fact "the number of ones in the codeword is even" error correction is also possible, for example for the $\text{SPC (5, 4, 2)}$: | |
:<math>\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) | :<math>\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) | ||
| Line 106: | Line 106: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ Also with [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input|AWGN channel]] error correction is possible when applying <i>Soft Decision</i> . For the following we assume bipolar signaling: |
| − | [[File:P ID2387 KC T 1 3 S1d v2.png|right|frame| | + | [[File:P ID2387 KC T 1 3 S1d v2.png|right|frame|To clarify "soft decision" at AWGN|class=fit]] |
| − | *$x=0$ ⇒ $\tilde{x}= +1$, | + | *$x=0$ ⇒ $\tilde{x}= +1$, as well as |
*$x=1$ ⇒ $\tilde{x}= -1$.<br> | *$x=1$ ⇒ $\tilde{x}= -1$.<br> | ||
| − | + | The graphic illustrates the facts presented here: | |
| − | * | + | *For example, the receive vector is (red dots): |
::<math>\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.</math> | ::<math>\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.</math> | ||
| − | * | + | *With a hard decision (threshold $G = 0$, only the signs are evaluated) one would arrive at the following binary result $($green squares $Y_i = y_i/ \vert y_i \vert)$: |
::<math>\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.</math> | ::<math>\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.</math> | ||
<br clear=all> | <br clear=all> | ||
| − | *In | + | *In symbol notation, this gives $(0, 1, 1, 0, 1)$, which is not a valid codeword of $\text{SPC (5, 4, 2)}$ ⇒ syndrome $s = 1$. So one, three or five bits must have been corrupted.<br> |
| − | * | + | *The probability for three or five bit errors, however, is orders of magnitude smaller than that for a single error. The assumption of "one bit error" is therefore not unreasonable.<br> |
| − | * | + | *Since the received value $y_3$ is very close to the threshold $G = 0$ it is assumed that exactly this bit has been corrupted. |
| − | * | + | *Thus, in <i>Soft Decision</i>, the decision is for $\underline{z} = (0, 1, 0, 0, 1)$ ⇒ $\underline{v} = (0, 1, 0, 0)$. |
| − | * | + | *The block error probability ${\rm Pr}(\underline{v} \ne \underline{u})$ is thus lowest.}}<br><br> |
| − | == | + | == Repetition Codes== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
Revision as of 18:00, 29 May 2022
Single Parity Check Codes
The Single Parity Check Code (SPC) adds to the information block $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ a parity bit $p$ :
- $$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$
- $$\Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.$$
The graphic shows three coding examples:
- $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \ (k = 2)$,
- $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \ (k = 3)$,
- $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \ (k = 4)$.
This very simple code can be characterized as follows:
- From $n = k + 1$ follows for the code rate $R = k/n = (n-1)/n$ and for the redundancy $1-R = 1/n$. For $k = 2$ , for example, the code rate is $2/3$ and the relative redundancy is $33.3\%$.
- The parity bit is obtained by modulo–2–addition. This is the addition in the Galois field to the base $2$ ⇒ $\rm GF(2)$, so that $1 \oplus 1 = 0$ results:
- \[p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.\]
- Thus every valid codeword $\underline{x}$ contains an even number of ones. Expressed as $\oplus$ or in simplified notation according to the second equation, this condition reads:
- \[ x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm or:}\hspace{0.5cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}. \]
- For $k = 2$ ⇒ $n = 3$ the following four code words result, where the parity bit $p$ is marked by a small arrow in each case:
- \[\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.\]
- This code $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$ is linear since the sum of any two codewords again gives a valid codeword, for example.
- $$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$
- For any $k$ ⇒ $n = k+1$ each codeword differs from all others at an even number of positions. Thus, the minimum distance of the code is
- $$d_{\rm min} = 2.$$
$\text{Definition:}$ Each $\text{Single Parity Check Code (SPC)}$ can be formally described as follows:
- \[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm with \hspace{0.15cm}even\hspace{0.15cm} number\hspace{0.15cm} of\hspace{0.15cm} ones\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.\]
- With the general code name $(n, \ k, \ d_{\rm min})$ any Single Parity–check Code can also be named $\text{SPC }(n, \ n-1, \ 2)$ .
- The top graph thus shows the $\text{SPC (3, 2, 2)}$, the $\text{SPC (4, 3, 2)}$, and the $\text{SPC (5, 4, 2)}$.
The digital channel may change the codeword $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$ to the receive word $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. With the error vector $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$ holds:
- $$\underline{y}= \underline{x} \oplus \underline{e}.$$
For decoding the Single Parity Check Code one forms the so-called syndrome:
- \[s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.\]
The result $s=1$ then indicates (at least) one bit error within the codeword, while $s=0$ should be interpreted as follows:
- The transmission was error-free, or:
- The number of bit errors is even.
$\text{Example 1:}$ We consider the $\text{SPC (4, 3, 2)}$ and assume that the null word was sent. The table shows all possibilities that $f$ bits are corrupted and gives the respective syndrome $s \in \{0, 1\}$ .
For the BSC model with the crossover probability (Noah) $\varepsilon = 1\%$ the following probabilities then result:
- The information word is correctly decoded (blue background):
- \[{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.\]
- The decoder detects that transmission errors have occurred (green background):
- \[{\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.\]
- The information word is decoded incorrectly (red background):
- \[{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.\]
We refer here to the interactive applet Binomial and Poisson Distribution. The results obtained here are also discussed again in the Exercise A1.5
$\text{Example 2:}$ Error correction of the single parity–check code is not possible for the BSC–model unlike the BEC–channel (Binary Erasure Channel).
Bit errors are excluded with this one. If only one bit is erased $($ erasure, $\rm E)$, then due to the fact "the number of ones in the codeword is even" error correction is also possible, for example for the $\text{SPC (5, 4, 2)}$:
\[\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},\] \[\underline{y}=(0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},\] \[\underline{y} = (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.\]
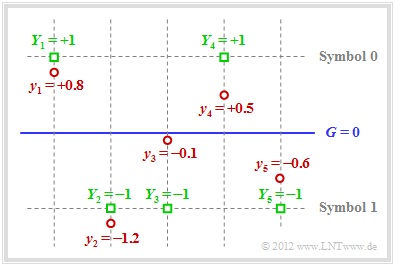
$\text{Example 3:}$ Also with AWGN channel error correction is possible when applying Soft Decision . For the following we assume bipolar signaling:
- $x=0$ ⇒ $\tilde{x}= +1$, as well as
- $x=1$ ⇒ $\tilde{x}= -1$.
The graphic illustrates the facts presented here:
- For example, the receive vector is (red dots):
- \[\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.\]
- With a hard decision (threshold $G = 0$, only the signs are evaluated) one would arrive at the following binary result $($green squares $Y_i = y_i/ \vert y_i \vert)$:
- \[\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.\]
- In symbol notation, this gives $(0, 1, 1, 0, 1)$, which is not a valid codeword of $\text{SPC (5, 4, 2)}$ ⇒ syndrome $s = 1$. So one, three or five bits must have been corrupted.
- The probability for three or five bit errors, however, is orders of magnitude smaller than that for a single error. The assumption of "one bit error" is therefore not unreasonable.
- Since the received value $y_3$ is very close to the threshold $G = 0$ it is assumed that exactly this bit has been corrupted.
- Thus, in Soft Decision, the decision is for $\underline{z} = (0, 1, 0, 0, 1)$ ⇒ $\underline{v} = (0, 1, 0, 0)$.
- The block error probability ${\rm Pr}(\underline{v} \ne \underline{u})$ is thus lowest.
Repetition Codes
$\text{Definition:}$ Ein $\text{Wiederholungscode}$ (englisch: Repetition Code, $\rm RC)$ ist ein linearer binärer $(n, \, k)$–Blockcode der Form
- \[\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.15cm}{\rm f\ddot{u}r \hspace{0.15cm}alle\hspace{0.25cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.\]
- Der Codeparameter $n$ bezeichnet die Codelänge. Unabhängig von $n$ gilt stets $k = 1$.
- Entsprechend existieren nur die zwei Codeworte $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$ und $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$, die sich in $n$ Binärstellen unterscheiden.
- Daraus folgt für die minimale Distanz $d_{\rm min} = n$.
Die Grafik zeigt Wiederholungscodes für
- $n=3$,
- $n=4$,
- $n=5$.
Ein solcher Wiederholungscode weist folgende Eigenschaften auf:
- Dieser $(n, \, 1, \, n)$–Blockcode besitzt die sehr kleine Coderate $R = 1/n$, ist also nur für die Übertragung bzw. Speicherung kleiner Dateien geeignet.
- Andererseits ist der Wiederholungscode sehr robust.
- Insbesondere beim BEC–Kanal (Binary Erasure Channel) genügt ein einziges richtig übertragenes Bit an beliebiger Position (alle anderen Bit können ausgelöscht sein), um das Informationswort richtig zu decodieren.
$\text{Beispiel 4: Decodierung und Fehlerwahrscheinlichkeiten beim BSC–Kanal}$
Es gelte der BSC–Kanal mit $\varepsilon = 10\%$. Die Decodierung basiere auf dem Majoritätsprinzip.
- Bei ungeradem $n$ können $e=n-1$ Bitfehler erkannt und $t=(n-1)/2$ Bitfehler korrigiert werden. Damit ergibt sich für die Wahrscheinlichkeit der korrekten Decodierung der Informationsbits $u$:
- \[{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.\]
- Die nachfolgenden Zahlenwerte gelten für $n = 5$. Das heißt: Es sind $t = 2$ Bitfehler korrigierbar:
- \[{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%\]
- \[\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.\]
- Bei geradem $n$ können dagegen nur $t=n/2-1$ Fehler korrigiert werden. Erhöht man $n$ von $5$ auf $6$, so sind weiterhin auch nur zwei Bitfehler innerhalb eines Codewortes korrigierbar. Einen dritten Bitfehler kann man zwar nicht korrigieren, aber zumindest erkennen:
- \[{\rm Pr}({\rm nicht\hspace{0.15cm} korrigierbarer\hspace{0.15cm} Fehler}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}. \]
- Ein (unerkannter) Decodierfehler $(v \ne u)$ ergibt sich erst, wenn innerhalb des 6 Bit–Wortes vier oder mehr Bit verfälscht wurden. Als Näherung unter der Annahme, dass fünf oder sechs Bitfehler sehr viel unwahrscheinlicher sind als vier, gilt:
- \[{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.\]
- Interessant ist, dass beim $\text{RC(6, 1, 6)}$ die Wahrscheinlichkeit ${\rm Pr}(v = u)$ für eine mögliche und richtige Decodierung mit $98.42\%$ kleiner ist als beim $\text{RC (5, 1, 5)}$. Für letzteren gilt:
- $${\rm Pr}(v = u) = 1- 0.00122 \approx 99.88\%.$$
$\text{Beispiel 5: Leistungsfähigkeit des Wiederholungscodes beim AWGN–Kanal}$
Wir betrachten nun den AWGN–Kanal. Bei uncodierter Übertragung $($oder dem Wiederholungscode mit $n=1)$ ist der Empfangswert $y = \tilde{x}+\eta$, wobei $\tilde{x} \in \{+1, -1\}$ das Informationsbit bei bipolarer Signalisierung bezeichnet und $\eta$ den Rauschterm. Um Verwechslungen mit dem Codeparameter $n$ zu vermeiden, haben wir das Rauschen umbenannt: $n → \eta$.
Für die Fehlerwahrscheinlichkeit gilt mit dem komplementären Gaußschen Fehlerintegral ${\rm Q}(x)$
- \[{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},\]
wobei folgende physikalische Größen zu verwenden sind:
- das Signal–zu–Rauschleistungsverhältnis $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,
- die Energie $E_{\rm S}$ pro Codesymbol ⇒ "Symbolenergie",
- die normierte Streuung $\sigma$ des Rauschens, gültig für das bipolare Informationsbit $\tilde{x} \in \{+1, -1\}$, und
- die konstante (einseitige) Rauschleistungsdichte $N_0$ des AWGN–Rauschens.
Bei einem $(n, 1, n)$–Wiederholungscode ergibt sich dagegen für den Eingangswert des Maximum–Likelihood–Decoders $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$ mit folgenden Eigenschaften:
- \[\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Amplitude}\]
- \[\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fache \hspace{0.15cm}Leistung}\hspace{0.05cm},\]
- \[\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Varianz:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},\]
- \[\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.\]
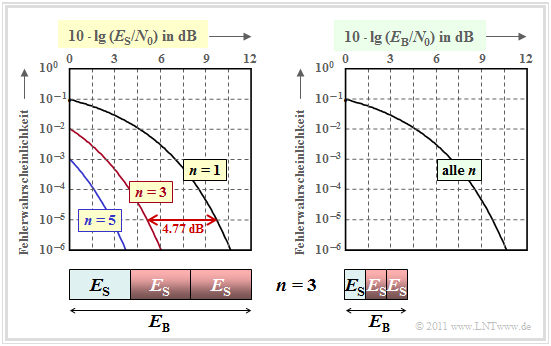
Die Fehlerwahrscheinlichkeit in doppelt logarithmischer Darstellung zeigt die linke Grafik. Als Abszisse ist $10 \cdot \lg \, (E_{\rm S}/N_0)$ aufgetragen. Die Energie pro Bit $(E_{\rm B})$ ist $n$ mal größer als die Symbolenergie $E_{\rm S}$, wie im Schaubild für $n=3$ verdeutlicht.
Diese Kurvenschar kann wie folgt interpretiert werden:
- Trägt man die Fehlerwahrscheinlichkeit über der Abszisse $10 \cdot \lg \, (E_{\rm S}/N_0)$ auf, so ergibt sich durch $n$–fache Wiederholung gegenüber uncodierter Übertragung $(n=1)$ eine signifikante Verbesserung.
- Die Kurve für den Wiederholungsfaktor $n$ erhält man durch Linksverschiebung um $10 \cdot \lg \, n$ (in dB) gegenüber der Vergleichskurve. Der Gewinn beträgt $4.77 \ {\rm dB} \ (n = 3)$ bzw. $\approx 5 \ {\rm dB} \ (n = 5)$.
- Allerdings ist ein Vergleich bei konstantem $E_{\rm S}$ nicht fair, da man mit dem Repetition Code $\text{RC (5, 1, 5)}$ für die Übertragung eines Informationsbits eine um den Faktor $n$ größere Energie aufwendet als bei uncodierter Übertragung: $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$
Aus der rechten Grafik erkennt man, dass alle Kurven genau übereinander liegen, wenn auf der Abszisse $10 \cdot \lg \, (E_{\rm B}/N_0)$ aufgetragen wird.
$\text{Fazit bezüglich Wiederholungscodes beim AWGN–Kanal:}$
- Die Fehlerwahrscheinlichkeit ist bei fairem Vergleich unabhängig vom Wiederholungsfaktor $n$: ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) \hspace{0.05cm}.$
- Beim AWGN–Kanal ist durch einen Wiederholungscode kein Codiergewinn zu erzielen.
Hamming codes
Richard Wesley Hamming hat 1962 eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl $m = 2, 3, \text{...} $ der zugesetzten Parity Bits unterscheiden. Für diese Codeklasse gilt:
- Die Codelänge ergibt sich stets zu $n = 2^m -1$. Möglich sind demzufolge beim Hamming–Code auch nur die Längen $n = 3$, $n = 7$, $n = 15$, $n = 31$, $n = 63$, $n = 127$, $n = 255$, usw.
- Ein Informationswort besteht aus $k = n-m$ Bit. Die Coderate ist somit gleich
- \[R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} \text{...} \hspace{0.05cm} \}\hspace{0.05cm}.\]
- Alle Hamming–Codes weisen die minimale Distanz $d_{\rm min} = 3$ auf. Bei größerer Codelänge $n$ erreicht man $d_{\rm min} = 3$ schon mit weniger Redundanz, also bei größerer Coderate $R$.
- Aus der Angabe $d_{\rm min} = 3$ folgt weiter, dass hier $e = d_{\rm min} -1 =2$ Fehler erkannt werden können und man $t = (d_{\rm min} -1)/2 = 1$ Fehler korrigieren kann.
- Der Hamming–Code $\text{HC (3, 1, 3)}$ ist identisch mit dem Wiederholungscode $\text{RP (3, 1, 3)}$ und lautet:
- \[\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.05cm}, (1, 1, 1) \big \}\hspace{0.05cm}. \]
- Bei systematischer Codierung sind die ersten $k$ Stellen eines jeden Hamming–Codewortes $\underline{x}$ identisch mit dem Informationswort $\underline{u}$. Anschließend folgen dann die $m = n-k$ Paritätsbit:
- \[\underline{x} = ( x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) = ( u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k}) \hspace{0.05cm}.\]
$\text{Beispiel 6: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$
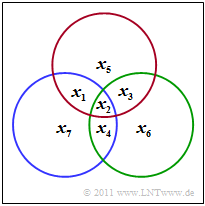
Der $\text{(7, 4, 3)}$–Hamming–Code wird durch das dargestellte Schaubild verdeutlicht. Daraus kann man die drei Bedingungen ableiten:
- \[x_1 \oplus x_2 \oplus x_3 \oplus x_5 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\]
- \[x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\]
- \[x_1 \oplus x_2 \oplus x_4 \oplus x_7 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm}. \]
- Im Schaubild kennzeichnet der rote Kreis die erste Prüfgleichung, der grüne die zweite und der blaue die letzte.
- In jedem Kreis muss die Anzahl der Einsen geradzahlig sein.
Bei systematischer Codierung des $\text{(7, 4, 3)}$–Hamming–Codes
- \[x_1 = u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm} x_5 = p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3 \]
lauten die Bestimmungsgleichungen der drei Prüfbit, wie aus dem Schaubild hervorgeht:
- \[p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},\]
- \[p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},\]
- \[p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.\]
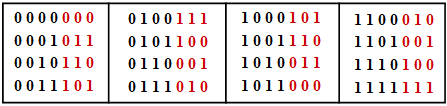
Die Tabelle zeigt die $2^k = 16$ zulässigen Codeworte des systematischen $\text{(7, 4, 3)}$–Codes:
- $$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3).$$
- Das Informationswort $\underline{u} =( u_1, u_2, u_3, u_4)$ ist schwarz dargestellt und die Prüfbits $p_1$, $p_2$ und $p_3$ rot.
- Man erkennt anhand dieser Tabelle, dass sich jeweils zwei der $16$ möglichen Codeworte in mindestens $d_{\rm min} = 3$ Binärwerten unterscheiden.
Später wird die Decodierung linearer Blockcodes noch ausführlich behandelt. Das folgende Beispiel soll die Decodierung des Hamming–Codes eher intuitiv erklären.
$\text{Beispiel 7: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$
Wir gehen weiter vom systematischen $\text{(7, 4, 3)}$–Code aus und betrachten das Empfangswort $\underline{y} = ( y_1, y_2, y_3, y_4, y_5, y_6, y_7)$. Zur Decodierung bilden wir die drei Paritätsgleichungen
- \[ y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} \]
- \[y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)} \]
- \[y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}\]
Unter der Voraussetzung, dass in jedem Codewort höchstens ein Bit verfälscht wird, gelten dann die folgenden Aussagen. Im Folgenden bezeichnet $\underline{v}$ das Decodierergebnis; dieses sollte stets mit $\underline{u} = (1, 0, 1, 0)$ übereinstimmen:
- Das Empfangswort $\underline{y} = (1, 0, 1, 0, 0, 1, 1)$ erfüllt alle drei Paritätsgleichungen. Das heißt, dass kein einziger Übertragungsfehler aufgetreten ist ⇒ $\underline{y} = \underline{x}$ ⇒ $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
- Werden zwei der drei Paritätsgleichungen erfüllt wie zum Beispiel für das empfangene Wort $\underline{y} =(1, 0, 1, 0, 0, 1, 0)$, so wurde ein Paritätsbit verfälscht und es gilt auch hier $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
- Mit $\underline{y} = (1, 0, 1, 1, 0, 1, 1)$ wird nur die Gleichung $\rm (I)$ erfüllt und die beiden anderen nicht. Somit kann man die Verfälschung des vierten Binärsymbols korrigieren, und es gilt auch hier $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
- Ein Übertragungsfehler des zweiten Bits ⇒ $\underline{y} = (1, 1, 1, 0, 0, 1, 1)$ führt dazu, dass alle drei Paritätsgleichungen nicht erfüllt werden. Auch dieser Fehler lässt sich eindeutig korrigieren da nur $u_2$ in allen Gleichungen vorkommt.
Aufgaben zum Kapitel
Aufgabe 1.5: SPC (5, 4) und BEC–Modell
Aufgabe 1.5Z: SPC (5, 4) vs. RC (5, 1)
Aufgabe 1.6: Zum (7, 4)–Hamming–Code