Difference between revisions of "Aufgaben:Exercise 3.1: Impulse Response of the Coaxial Cable"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/3.1 Ursachen/Auswirkungen von Impulsinterferenzen [[File:|right|]] ===Fragebogen=== <quiz display=simp…“) |
m (Guenter moved page Exercise 3.1: Impulse response of the Coaxial Cable to Exercise 3.1: Impulse Response of the Coaxial Cable) |
||
| (59 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference |
| + | }} | ||
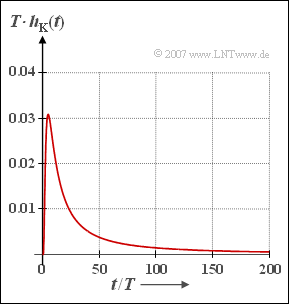
| + | [[File:P_ID1370__Dig_A_3_1.png|right|frame|Impulse response of a coaxial cable]] | ||
| + | The frequency response of a coaxial cable of length $l$ can be represented by the following formula: | ||
| + | :$$H_{\rm K}(f) \ = \ {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} | ||
| + | \cdot | ||
| + | {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot | ||
| + | \ {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | *The first term of this equation is due to the ohmic losses. | |
| + | * The second term is due to the transverse losses. | ||
| + | *Dominant, however, is the skin effect, which is expressed by the third term. | ||
| − | === | + | With the coefficients valid for a so-called "standard coaxial cable" $(2.6 \ \rm mm$ core diameter and $9.5 \ \rm mm$ outer diameter$)$ |
| + | :$$\alpha_2 = 0.2722 \hspace{0.15cm}\frac{\rm Np}{\rm km \cdot \sqrt{\rm MHz}} | ||
| + | \hspace{0.05cm}, | ||
| + | \hspace{0.2cm} \beta_2 = 0.2722 \hspace{0.15cm}\frac{\rm rad}{\rm km \cdot \sqrt{\rm MHz}}\hspace{0.05cm},$$ | ||
| + | |||
| + | the frequency response can also be represented as follows: | ||
| + | :$$H_{\rm K}(f) \approx {\rm e}^{- 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} | ||
| + | \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}} } \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} | ||
| + | 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} | ||
| + | \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | That means: Attenuation curve $a_{\rm K}(f)$ and phase curve $b_{\rm K}(f)$ are identical except for the pseudo units "$\rm Np$" and "$\rm rad$". | ||
| + | |||
| + | If one defines the characteristic cable attenuation $a_*$ at half the bit rate $(R_{\rm B}/2)$, one can treat digital systems of different bit rate and length uniformly: | ||
| + | :$$a_{\star} = a_{\rm K}(f = {R_{\rm B}}/{2}) | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- | ||
| + | a_{\star} \cdot \sqrt{2f/R_{\rm | ||
| + | B}}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} a_{\star} \cdot \sqrt{2f/R_{\rm | ||
| + | B}}}\hspace{0.4cm}{\rm with}\hspace{0.2cm}a_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | The corresponding $\rm dB$ value is larger by a factor of $8.688$. For a binary system, $R_{\rm B} = 1/T$ applies, so that the characteristic cable attenuation is then related to the frequency $f = 1/(2T)$. | ||
| + | |||
| + | |||
| + | The Fourier transform of $H_{\rm K}(f)$ yields the impulse response $h_{\rm K}(t)$, which can be given in closed-analytic form for a coaxial cable with the approximations described here. For a binary system holds: | ||
| + | :$$h_{\rm K}(t) = \frac{ a_{\star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot | ||
| + | {\rm exp} \left[ - \frac{a_{\star}^2}{2 \pi \cdot t/T}\hspace{0.1cm}\right] | ||
| + | \hspace{0.4cm}{\rm with}\hspace{0.2cm}a_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Subtask '''(5)''' is related to the basic receiver pulse $g_r(t) = g_s(t) * h_K(t)$, where $g_s(t)$ should be assumed to be a rectangular pulse with height $s_0$ and duration $T$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference|"Causes and Effects of Intersymbol Interference"]]. | ||
| + | |||
| + | *Reference is made in particular to the section [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the length $l$ of a standard coaxial cable, if for the bit rate $R_{\rm B} = 140 \ \rm Mbit/s$ the characteristic cable attenuation is $a_* = 60 \ \rm dB$? |
| − | |type=" | + | |type="{}"} |
| − | + | $l \ = \ $ { 3 3% } $\ \rm km $ | |
| − | |||
| + | {At what time $t_{\rm max}$ does $h_{\rm K}(t)$ have its maximum? Let $a_* = 60 \ \rm dB$ be further valid. | ||
| + | |type="{}"} | ||
| + | $t_{\rm max}/T= \ $ { 5 3% } | ||
| − | { | + | {What is the maximum value of the impulse response? Let $a_* = 60 \ \rm dB$ continue to hold. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\rm Max}\ \big [h_{\rm K}(t)\big ]= \ $ { 0.03 3% } $\ \cdot 1/T $ |
| − | |||
| + | {At what time $t_{\rm 5\%}$ is $h_{\rm K}(t)$ less than $5\%$ of the maximum? Consider only the first term of the given formula as an approximation. | ||
| + | |type="{}"} | ||
| + | $t_{\rm 5\%}/T= \ $ { 103.5 3% } | ||
| + | {Which statements are true for the basic receiver pulse $g_r(t)$? | ||
| + | |type="[]"} | ||
| + | - $g_r(t)$ is twice as wide as $h_{\rm K}(t)$. | ||
| + | + It is approximately $g_r(t) = h_{\rm K}(t) \cdot s_0 \cdot T$. | ||
| + | - $g_r(t)$ can be approximated by a Gaussian pulse. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The characteristic cable attenuation $a_* = 60 \ \rm dB$ corresponds to about $6.9 \ \rm Np$. Therefore, it must hold: |
| − | '''(2)''' | + | :$$\alpha_2 \cdot l \cdot {R_{\rm B}}/{2} = 6.9\,\,{\rm |
| − | + | Np}$$ | |
| − | + | :$$\Rightarrow \hspace{0.3cm} l = \frac{6.9\,\,{\rm | |
| − | + | Np}}{0.2722\,\,\frac{\rm Np}{{\rm km} \cdot \sqrt{\rm MHz}} | |
| − | + | \cdot \sqrt{70\,\,{\rm MHz}}} \hspace{0.15cm}\underline {\approx 3\,\,{\rm km}} | |
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' With the substitutions | ||
| + | :$$x = { t}/{ T}, \hspace{0.2cm} K_1 = \frac{a_*/T}{\sqrt{2\pi^2 }}, \hspace{0.2cm} | ||
| + | K_2 = \frac{a_*^2}{2\pi}$$ | ||
| + | |||
| + | the impulse response can be described as follows: | ||
| + | :$$h_{\rm K}(x) = K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *By setting the derivative to zero, it follows: | ||
| + | :$$- {3}/{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm | ||
| + | e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 | ||
| + | \hspace{0.05cm}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {3}/{2} \cdot x^{-5/2} = K_2 \cdot | ||
| + | x^{-7/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | x_{\rm max} = {2}/{3} \cdot K_2 = { a_{\star}^2}/({3 \pi}) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *This gives for $60 \ \rm dB$ cable attenuation $(a_* ≈ 6.9 \ \rm Np)$: | ||
| + | :$$x_{\rm max} = { t_{\rm max}}/{ T} \hspace{-0.1cm}: \hspace{0.2cm} { t_{\rm max}}/{ T} = { 6.9^2}/({3\pi})\hspace{0.15cm}\underline {\approx 5} \hspace{0.2cm}.$$ | ||
| + | |||
| + | '''(3)''' Substituting the result of '''(2)''' into the given equation, we obtain (using $a$ instead of $a_*$): | ||
| + | :$$h_{\rm K}(t_{\rm max}) \ = \ \frac{1}{T} \cdot \frac{ a}{ \sqrt{2 \pi^2 \cdot \frac{a^6}{(3\pi)^3}}}\hspace{0.1cm} \cdot | ||
| + | {\rm exp} \left[ - \frac{a^2}{2\pi} \cdot | ||
| + | \frac{3\pi}{a^2}\hspace{0.1cm}\right]= \frac{1}{T} \cdot \frac{1}{a^2}\cdot | ||
| + | \sqrt{\frac{27 \pi | ||
| + | }{2}} \cdot {\rm e}^{-3/2}\hspace{0.15cm}\approx \frac{1}{T} \cdot \frac{1.453}{a^2} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Thus, with $a = 6.9$, we arrive at the final result: | ||
| + | :$${\rm Max} \ [h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline {\approx 0.03 \cdot {1}/{T}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Using the result of subtask '''(3)''', the determining equation is: | ||
| + | :$$\frac{ a/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 \cdot {1}/{T}= 0.0015 \cdot {1}/{T} \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} (t_{5\%}/T)^{3/2} = \frac{a}{\sqrt{2} \cdot \pi \cdot | ||
| + | 0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow | ||
| + | \hspace{0.3cm}t_{5\%}/T \hspace{0.15cm}\underline {\approx 103.5}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *This value is slightly too large because the second term ${\rm e}^{\rm – 0.05} ≈ 0.95$ was neglected. | ||
| + | *The exact calculation gives $t_{\rm 5\%}/T ≈ 97$. | ||
| + | |||
| + | |||
| + | '''(5)''' The <u>second solution</u> is correct. In general: | ||
| + | :$$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot | ||
| + | \int_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$ | ||
| + | |||
| + | *Since the channel impulse response $h_{\rm K}(t)$ changes only insignificantly within a symbol duration, it can also be written for this purpose: | ||
| + | :$$g_r(t) \approx h_{\rm K}(t) \cdot s_0 \cdot T .$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | + | [[Category:Digital Signal Transmission: Exercises|^3.1 Intersymbol Interference^]] | |
| − | [[Category: | ||
Latest revision as of 13:59, 31 May 2022
The frequency response of a coaxial cable of length $l$ can be represented by the following formula:
- $$H_{\rm K}(f) \ = \ {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot \ {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
- The first term of this equation is due to the ohmic losses.
- The second term is due to the transverse losses.
- Dominant, however, is the skin effect, which is expressed by the third term.
With the coefficients valid for a so-called "standard coaxial cable" $(2.6 \ \rm mm$ core diameter and $9.5 \ \rm mm$ outer diameter$)$
- $$\alpha_2 = 0.2722 \hspace{0.15cm}\frac{\rm Np}{\rm km \cdot \sqrt{\rm MHz}} \hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722 \hspace{0.15cm}\frac{\rm rad}{\rm km \cdot \sqrt{\rm MHz}}\hspace{0.05cm},$$
the frequency response can also be represented as follows:
- $$H_{\rm K}(f) \approx {\rm e}^{- 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}} } \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} \hspace{0.05cm}.$$
That means: Attenuation curve $a_{\rm K}(f)$ and phase curve $b_{\rm K}(f)$ are identical except for the pseudo units "$\rm Np$" and "$\rm rad$".
If one defines the characteristic cable attenuation $a_*$ at half the bit rate $(R_{\rm B}/2)$, one can treat digital systems of different bit rate and length uniformly:
- $$a_{\star} = a_{\rm K}(f = {R_{\rm B}}/{2}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- a_{\star} \cdot \sqrt{2f/R_{\rm B}}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} a_{\star} \cdot \sqrt{2f/R_{\rm B}}}\hspace{0.4cm}{\rm with}\hspace{0.2cm}a_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
The corresponding $\rm dB$ value is larger by a factor of $8.688$. For a binary system, $R_{\rm B} = 1/T$ applies, so that the characteristic cable attenuation is then related to the frequency $f = 1/(2T)$.
The Fourier transform of $H_{\rm K}(f)$ yields the impulse response $h_{\rm K}(t)$, which can be given in closed-analytic form for a coaxial cable with the approximations described here. For a binary system holds:
- $$h_{\rm K}(t) = \frac{ a_{\star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{a_{\star}^2}{2 \pi \cdot t/T}\hspace{0.1cm}\right] \hspace{0.4cm}{\rm with}\hspace{0.2cm}a_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
Subtask (5) is related to the basic receiver pulse $g_r(t) = g_s(t) * h_K(t)$, where $g_s(t)$ should be assumed to be a rectangular pulse with height $s_0$ and duration $T$.
Notes:
- The exercise belongs to the chapter "Causes and Effects of Intersymbol Interference".
- Reference is made in particular to the section "Signals, Basis Functions and Vector Spaces".
Questions
Solution
- $$\alpha_2 \cdot l \cdot {R_{\rm B}}/{2} = 6.9\,\,{\rm Np}$$
- $$\Rightarrow \hspace{0.3cm} l = \frac{6.9\,\,{\rm Np}}{0.2722\,\,\frac{\rm Np}{{\rm km} \cdot \sqrt{\rm MHz}} \cdot \sqrt{70\,\,{\rm MHz}}} \hspace{0.15cm}\underline {\approx 3\,\,{\rm km}} \hspace{0.05cm}.$$
(2) With the substitutions
- $$x = { t}/{ T}, \hspace{0.2cm} K_1 = \frac{a_*/T}{\sqrt{2\pi^2 }}, \hspace{0.2cm} K_2 = \frac{a_*^2}{2\pi}$$
the impulse response can be described as follows:
- $$h_{\rm K}(x) = K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x} \hspace{0.05cm}.$$
- By setting the derivative to zero, it follows:
- $$- {3}/{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} {3}/{2} \cdot x^{-5/2} = K_2 \cdot x^{-7/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x_{\rm max} = {2}/{3} \cdot K_2 = { a_{\star}^2}/({3 \pi}) \hspace{0.05cm}.$$
- This gives for $60 \ \rm dB$ cable attenuation $(a_* ≈ 6.9 \ \rm Np)$:
- $$x_{\rm max} = { t_{\rm max}}/{ T} \hspace{-0.1cm}: \hspace{0.2cm} { t_{\rm max}}/{ T} = { 6.9^2}/({3\pi})\hspace{0.15cm}\underline {\approx 5} \hspace{0.2cm}.$$
(3) Substituting the result of (2) into the given equation, we obtain (using $a$ instead of $a_*$):
- $$h_{\rm K}(t_{\rm max}) \ = \ \frac{1}{T} \cdot \frac{ a}{ \sqrt{2 \pi^2 \cdot \frac{a^6}{(3\pi)^3}}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{a^2}{2\pi} \cdot \frac{3\pi}{a^2}\hspace{0.1cm}\right]= \frac{1}{T} \cdot \frac{1}{a^2}\cdot \sqrt{\frac{27 \pi }{2}} \cdot {\rm e}^{-3/2}\hspace{0.15cm}\approx \frac{1}{T} \cdot \frac{1.453}{a^2} \hspace{0.05cm}.$$
- Thus, with $a = 6.9$, we arrive at the final result:
- $${\rm Max} \ [h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline {\approx 0.03 \cdot {1}/{T}} \hspace{0.05cm}.$$
(4) Using the result of subtask (3), the determining equation is:
- $$\frac{ a/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 \cdot {1}/{T}= 0.0015 \cdot {1}/{T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} (t_{5\%}/T)^{3/2} = \frac{a}{\sqrt{2} \cdot \pi \cdot 0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}t_{5\%}/T \hspace{0.15cm}\underline {\approx 103.5}\hspace{0.05cm}.$$
- This value is slightly too large because the second term ${\rm e}^{\rm – 0.05} ≈ 0.95$ was neglected.
- The exact calculation gives $t_{\rm 5\%}/T ≈ 97$.
(5) The second solution is correct. In general:
- $$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot \int_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$
- Since the channel impulse response $h_{\rm K}(t)$ changes only insignificantly within a symbol duration, it can also be written for this purpose:
- $$g_r(t) \approx h_{\rm K}(t) \cdot s_0 \cdot T .$$