Difference between revisions of "Aufgaben:Exercise 2.3: Binary Signal and Quaternary Signal"
m (Guenter verschob die Seite 2.3 Binär- und Quaternärsignal nach 2.3 Binärsignal und Quaternärsignal) |
|||
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Redundancy-Free_Coding |
}} | }} | ||
| − | [[File:P_ID1324__Dig_A_2_3.png|right|frame| | + | [[File:P_ID1324__Dig_A_2_3.png|right|frame|ACF and PSD of binary signal $\rm (B)$ and quaternary signal $\rm (Q)$]] |
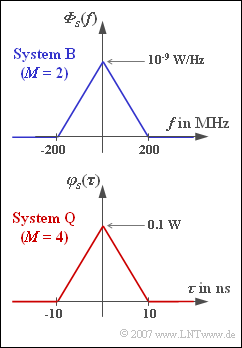
| − | + | Two redundancy-free transmission systems $\rm B$ and $\rm Q$ each with bipolar amplitude coefficients $a_{\nu}$ are to be compared. Both systems satisfy the first Nyquist condition. According to the root-root splitting, the spectrum $G_{d}(f)$ of the basic detection pulse is equal in shape to the power-spectral density ${\it \Phi}_{s}(f)$ of the transmitted signal. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The following properties of the two systems are known: | ||
| + | *From the binary system $\rm B$, the power-spectral density ${\it \Phi}_{s}(f)$ at the transmitter is known and shown in the graph together with the description parameters. | ||
| + | *The quaternary system $\rm Q$ uses a NRZ rectangular signal with the four possible amplitude values $±s_{0}$ and $±s_{0}/3$, all with equal probability. | ||
| − | + | *${s_{0}}^{2}$ indicates the maximum instantaneous power that occurs only when one of the two "outer symbols" is transmitted. The descriptive parameters of system $\rm Q$ can be obtained from the triangular ACF in the adjacent graph. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | Notes: | ||
| + | *The exercise is part of the chapter [[Digital_Signal_Transmission/Grundlagen_der_codierten_Übertragung|"Basics of Coded Transmission"]]. | ||
| + | |||
| + | *Reference is also made to the chapter [[Digital_Signal_Transmission/Redundanzfreie_Codierung|"Redundancy-Free Coding"]]. | ||
| + | |||
| + | *Consider that auto-correlation function $\rm (ACF)$ and power-spectral density $\rm (PSD)$ of a stochastic signal are always related via the Fourier transform. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the symbol duration $T$ of the binary system $\rm B$ with Nyquist property? |
|type="{}"} | |type="{}"} | ||
$T \ = \ $ { 5 3% } $\ \rm ns$ | $T \ = \ $ { 5 3% } $\ \rm ns$ | ||
| − | { | + | {What is the (equivalent) bit rate $R_{\rm B}$ of the binary system $\rm B$ ? |
|type="{}"} | |type="{}"} | ||
$R_{\rm B} \ = \ $ { 200 3% } $\ \rm Mbit/s$ | $R_{\rm B} \ = \ $ { 200 3% } $\ \rm Mbit/s$ | ||
| − | { | + | {What is the transmitted power of the binary system $\rm B$? |
|type="{}"} | |type="{}"} | ||
$P_{\rm S} \ = \ $ { 200 3% } $\ \rm mW$ | $P_{\rm S} \ = \ $ { 200 3% } $\ \rm mW$ | ||
| − | { | + | {Which statements are true regarding the binary system $\rm B$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The ACF $\varphi_{s}(\tau)$ of the transmitted signal is $\rm sinc^{2}$–shaped. |
| − | + | + | + The energy ACF $\varphi^{^{\bullet}}_{gs}(\tau)$ of the basic transmission pulse is $\rm sinc^{2}$–shaped. |
| − | - | + | - The basic transmission pulse $g_{s}(t)$ itself is $\rm sinc^{2}$–shaped. |
| − | { | + | {What is the symbol duration $T$ of the quaternary system $\rm Q$? |
|type="{}"} | |type="{}"} | ||
$T \ = \ $ { 10 3% } $\ \rm ns$ | $T \ = \ $ { 10 3% } $\ \rm ns$ | ||
| − | { | + | {What is the equivalent bit rate $R_{\rm B}$ of the quaternary system $\rm Q$? |
|type="{}"} | |type="{}"} | ||
$R_{\rm B} \ = \ $ { 200 3% } $\ \rm Mbit/s$ | $R_{\rm B} \ = \ $ { 200 3% } $\ \rm Mbit/s$ | ||
| − | { | + | {What is the transmitted power $P_{\rm S}$ of the quaternary system $\rm Q$? |
|type="{}"} | |type="{}"} | ||
$P_{\rm S} \ = \ $ { 100 3% } $\ \rm mW$ | $P_{\rm S} \ = \ $ { 100 3% } $\ \rm mW$ | ||
| − | { | + | {What is the maximum instantaneous transmitted power of the quaternary system $\rm Q$? |
|type="{}"} | |type="{}"} | ||
${s_{0}}^{2} \ = \ $ { 180 3% } $\ \rm mW$ | ${s_{0}}^{2} \ = \ $ { 180 3% } $\ \rm mW$ | ||
| Line 66: | Line 71: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The Nyquist frequency $f_{\rm Nyq} = 100 \ \rm MHz$ can be read from the diagram. From this follows according to the properties of Nyquist systems: |
:$$f_{\rm Nyq} = \frac{1 } {2 \cdot T} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T = \frac{1 } {2 \cdot f_{\rm Nyq}} \hspace{0.15cm}\underline{ =5\,{\rm ns}}\hspace{0.05cm}.$$ | :$$f_{\rm Nyq} = \frac{1 } {2 \cdot T} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T = \frac{1 } {2 \cdot f_{\rm Nyq}} \hspace{0.15cm}\underline{ =5\,{\rm ns}}\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | |
| + | '''(2)''' In the binary system, the bit rate is also the information flow and it holds: | ||
:$$R_{\rm B} = {1 }/ { T} \hspace{0.15cm}\underline {= 200\,{\rm Mbit/s}}= 2 \cdot f_{\rm Nyq} \cdot{\rm bit}/{\rm Hz}\hspace{0.05cm}.$$ | :$$R_{\rm B} = {1 }/ { T} \hspace{0.15cm}\underline {= 200\,{\rm Mbit/s}}= 2 \cdot f_{\rm Nyq} \cdot{\rm bit}/{\rm Hz}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| + | '''(3)''' The transmitted power is equal to the integral over ${\it \Phi}_{s}(f)$ and can be calculated as a triangular area: | ||
:$$P_{\rm S} = \ \int_{-\infty}^{+\infty} {\it \Phi}_s(f) \,{\rm d} f = 10^{-9} \frac{\rm W}{\rm Hz} \cdot 200\,\,{\rm MHz} \hspace{0.15cm}\underline { = 200\,\,{\rm mW}}.$$ | :$$P_{\rm S} = \ \int_{-\infty}^{+\infty} {\it \Phi}_s(f) \,{\rm d} f = 10^{-9} \frac{\rm W}{\rm Hz} \cdot 200\,\,{\rm MHz} \hspace{0.15cm}\underline { = 200\,\,{\rm mW}}.$$ | ||
| − | '''(4)''' | + | |
| − | * | + | '''(4)''' The <u>first two statements</u> are correct: |
| + | *The Fourier inverse transform of the power-spectral density ${\it \Phi}_{s}(f)$ gives the $\rm sinc^{2}$–shaped ACF $\varphi_{s}(\tau)$. In general, the following relationship also holds: | ||
:$$ \varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$ | :$$ \varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$ | ||
| − | * | + | *However, for a redundancy-free binary system, $\varphi_{a}(\lambda = 0) = 1$, while all other discrete ACF values $\varphi_{a}(\lambda \neq 0)$ are equal to $0$. Thus, the energy ACF also has a $\rm sinc^{2}$–shaped curve (note: energy ACF and energy PSD are each dotted in this tutorial): |
:$$\varphi^{^{\bullet}}_{gs}(\tau ) = T \cdot \varphi_s(\tau) \hspace{0.05cm}.$$ | :$$\varphi^{^{\bullet}}_{gs}(\tau ) = T \cdot \varphi_s(\tau) \hspace{0.05cm}.$$ | ||
| − | * | + | *The last statement is not true. For the following reasoning, we assume for simplicity that $g_{s}(t)$ is symmetric and thus $G_{s}(f)$ is real. Then holds: |
:$${\it \Phi}_{s}(f) = {1 }/ { T} \cdot |G_s(f)|^2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_s(f) = \sqrt{{ T} \cdot {\it \Phi}_{s}(f)}\hspace{0.4cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm}g_s(t) \hspace{0.05cm}.$$ | :$${\it \Phi}_{s}(f) = {1 }/ { T} \cdot |G_s(f)|^2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_s(f) = \sqrt{{ T} \cdot {\it \Phi}_{s}(f)}\hspace{0.4cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm}g_s(t) \hspace{0.05cm}.$$ | ||
| − | * | + | *Due to the square root in the above equation, the basic transmission pulse $g_{s}(t)$ is not $\rm sinc^{2}$–shaped in contrast to the basic detection pulse $g_{d}(t)$, which is equal in shape to the energy ACF $\varphi^{^{\bullet}}_{gs}(\tau)$ and thus $\rm sinc^{2}$–shaped. At the same time, $\varphi^{^{\bullet}}_{gs}(\tau) = g_{s}(\tau) ∗ g_{s}(–\tau)$ holds. |
| + | |||
| + | |||
| + | '''(5)''' The ACF $\varphi_{s}(\tau)$ is limited to the range $|\tau| ≤ T$ when the basic transmission pulse is an NRZ rectangle. From the graph, the symbol duration $T \underline{= 10 \ \rm ns}$. | ||
| − | |||
| − | '''(6)''' | + | '''(6)''' For the quaternary signal, the information flow is the same as for the binary signal above because of the double symbol duration: |
:$$R_{\rm B} = {{\rm log_2(4)} }/ { T} \hspace{0.15cm}\underline {= 200\,\,{\rm Mbit/s}}\hspace{0.05cm}.$$ | :$$R_{\rm B} = {{\rm log_2(4)} }/ { T} \hspace{0.15cm}\underline {= 200\,\,{\rm Mbit/s}}\hspace{0.05cm}.$$ | ||
| − | '''(7)''' | + | |
| + | '''(7)''' The transmitted power is equal to the ACF value at $\tau = 0$ and can be read from the graph: | ||
:$$P_{\rm S} = \hspace{0.15cm}\underline {100\,\,{\rm mW}}.$$ | :$$P_{\rm S} = \hspace{0.15cm}\underline {100\,\,{\rm mW}}.$$ | ||
| − | '''(8)''' | + | |
| + | '''(8)''' For the redundancy-free quaternary signal with NRZ rectangular pulses, the average transmitted power is: | ||
:$$P_{\rm S} = {1}/ { 4} \cdot \left [ (-s_0)^2 + (-s_0/3)^2 + (+s_0/3)^2 +(+s_0)^2 \right ] = {5}/ { 9} \cdot s_0^2$$ | :$$P_{\rm S} = {1}/ { 4} \cdot \left [ (-s_0)^2 + (-s_0/3)^2 + (+s_0/3)^2 +(+s_0)^2 \right ] = {5}/ { 9} \cdot s_0^2$$ | ||
:$$\Rightarrow \hspace{0.3cm}s_0^2 = {9}/ {5} \cdot P_{\rm S} = {9}/ {5} \cdot 100\,\,{\rm mW}\hspace{0.15cm}\underline { = 180\,\,{\rm mW}}\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm}s_0^2 = {9}/ {5} \cdot P_{\rm S} = {9}/ {5} \cdot 100\,\,{\rm mW}\hspace{0.15cm}\underline { = 180\,\,{\rm mW}}\hspace{0.05cm}.$$ | ||
| Line 103: | Line 115: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.2 Redundancy-Free Coding^]] |
Latest revision as of 16:16, 3 June 2022
Two redundancy-free transmission systems $\rm B$ and $\rm Q$ each with bipolar amplitude coefficients $a_{\nu}$ are to be compared. Both systems satisfy the first Nyquist condition. According to the root-root splitting, the spectrum $G_{d}(f)$ of the basic detection pulse is equal in shape to the power-spectral density ${\it \Phi}_{s}(f)$ of the transmitted signal.
The following properties of the two systems are known:
- From the binary system $\rm B$, the power-spectral density ${\it \Phi}_{s}(f)$ at the transmitter is known and shown in the graph together with the description parameters.
- The quaternary system $\rm Q$ uses a NRZ rectangular signal with the four possible amplitude values $±s_{0}$ and $±s_{0}/3$, all with equal probability.
- ${s_{0}}^{2}$ indicates the maximum instantaneous power that occurs only when one of the two "outer symbols" is transmitted. The descriptive parameters of system $\rm Q$ can be obtained from the triangular ACF in the adjacent graph.
Notes:
- The exercise is part of the chapter "Basics of Coded Transmission".
- Reference is also made to the chapter "Redundancy-Free Coding".
- Consider that auto-correlation function $\rm (ACF)$ and power-spectral density $\rm (PSD)$ of a stochastic signal are always related via the Fourier transform.
Questions
Solution
- $$f_{\rm Nyq} = \frac{1 } {2 \cdot T} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T = \frac{1 } {2 \cdot f_{\rm Nyq}} \hspace{0.15cm}\underline{ =5\,{\rm ns}}\hspace{0.05cm}.$$
(2) In the binary system, the bit rate is also the information flow and it holds:
- $$R_{\rm B} = {1 }/ { T} \hspace{0.15cm}\underline {= 200\,{\rm Mbit/s}}= 2 \cdot f_{\rm Nyq} \cdot{\rm bit}/{\rm Hz}\hspace{0.05cm}.$$
(3) The transmitted power is equal to the integral over ${\it \Phi}_{s}(f)$ and can be calculated as a triangular area:
- $$P_{\rm S} = \ \int_{-\infty}^{+\infty} {\it \Phi}_s(f) \,{\rm d} f = 10^{-9} \frac{\rm W}{\rm Hz} \cdot 200\,\,{\rm MHz} \hspace{0.15cm}\underline { = 200\,\,{\rm mW}}.$$
(4) The first two statements are correct:
- The Fourier inverse transform of the power-spectral density ${\it \Phi}_{s}(f)$ gives the $\rm sinc^{2}$–shaped ACF $\varphi_{s}(\tau)$. In general, the following relationship also holds:
- $$ \varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
- However, for a redundancy-free binary system, $\varphi_{a}(\lambda = 0) = 1$, while all other discrete ACF values $\varphi_{a}(\lambda \neq 0)$ are equal to $0$. Thus, the energy ACF also has a $\rm sinc^{2}$–shaped curve (note: energy ACF and energy PSD are each dotted in this tutorial):
- $$\varphi^{^{\bullet}}_{gs}(\tau ) = T \cdot \varphi_s(\tau) \hspace{0.05cm}.$$
- The last statement is not true. For the following reasoning, we assume for simplicity that $g_{s}(t)$ is symmetric and thus $G_{s}(f)$ is real. Then holds:
- $${\it \Phi}_{s}(f) = {1 }/ { T} \cdot |G_s(f)|^2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_s(f) = \sqrt{{ T} \cdot {\it \Phi}_{s}(f)}\hspace{0.4cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm}g_s(t) \hspace{0.05cm}.$$
- Due to the square root in the above equation, the basic transmission pulse $g_{s}(t)$ is not $\rm sinc^{2}$–shaped in contrast to the basic detection pulse $g_{d}(t)$, which is equal in shape to the energy ACF $\varphi^{^{\bullet}}_{gs}(\tau)$ and thus $\rm sinc^{2}$–shaped. At the same time, $\varphi^{^{\bullet}}_{gs}(\tau) = g_{s}(\tau) ∗ g_{s}(–\tau)$ holds.
(5) The ACF $\varphi_{s}(\tau)$ is limited to the range $|\tau| ≤ T$ when the basic transmission pulse is an NRZ rectangle. From the graph, the symbol duration $T \underline{= 10 \ \rm ns}$.
(6) For the quaternary signal, the information flow is the same as for the binary signal above because of the double symbol duration:
- $$R_{\rm B} = {{\rm log_2(4)} }/ { T} \hspace{0.15cm}\underline {= 200\,\,{\rm Mbit/s}}\hspace{0.05cm}.$$
(7) The transmitted power is equal to the ACF value at $\tau = 0$ and can be read from the graph:
- $$P_{\rm S} = \hspace{0.15cm}\underline {100\,\,{\rm mW}}.$$
(8) For the redundancy-free quaternary signal with NRZ rectangular pulses, the average transmitted power is:
- $$P_{\rm S} = {1}/ { 4} \cdot \left [ (-s_0)^2 + (-s_0/3)^2 + (+s_0/3)^2 +(+s_0)^2 \right ] = {5}/ { 9} \cdot s_0^2$$
- $$\Rightarrow \hspace{0.3cm}s_0^2 = {9}/ {5} \cdot P_{\rm S} = {9}/ {5} \cdot 100\,\,{\rm mW}\hspace{0.15cm}\underline { = 180\,\,{\rm mW}}\hspace{0.05cm}.$$