Difference between revisions of "Digital Signal Transmission/Burst Error Channels"
| Line 83: | Line 83: | ||
== Error distance distribution of the GE model == | == Error distance distribution of the GE model == | ||
<br> | <br> | ||
| − | [[File: | + | [[File:EN_Dig_T_5_3_S2.png|right|frame|Error distance distribution of GE and BSC model|class=fit]] |
In [Hub82]<ref name = 'Hub82'>Huber, J.: <i>Codierung für gedächtnisbehaftete Kanäle.</i> Dissertation – Universität der Bundeswehr München, 1982.</ref> you can find the analytical computations | In [Hub82]<ref name = 'Hub82'>Huber, J.: <i>Codierung für gedächtnisbehaftete Kanäle.</i> Dissertation – Universität der Bundeswehr München, 1982.</ref> you can find the analytical computations | ||
| Line 196: | Line 196: | ||
McCullough [McC68]<ref name ='McC68'>McCullough, R.H.: ''The Binary Regenerative Channel.'' In: Bell Syst. Techn. J. (47), 1968.</ref> modified the model developed three years earlier by Gilbert and Elliott so that an error distance simulation in the two states "GOOD" and "BAD" is applicable in each case by itself. The graph below shows McCullough's model, hereafter referred to as the '''MC model''', while the GE model is shown above after renaming the transition probabilities ⇒ ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, etc.<br> | McCullough [McC68]<ref name ='McC68'>McCullough, R.H.: ''The Binary Regenerative Channel.'' In: Bell Syst. Techn. J. (47), 1968.</ref> modified the model developed three years earlier by Gilbert and Elliott so that an error distance simulation in the two states "GOOD" and "BAD" is applicable in each case by itself. The graph below shows McCullough's model, hereafter referred to as the '''MC model''', while the GE model is shown above after renaming the transition probabilities ⇒ ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, etc.<br> | ||
| − | [[File: | + | [[File:EN_Dig_T_5_3_S4a.png|center|frame|Channel models according to Gilbert-Elliott (top) and McCullough (bottom)|class=fit]] |
There are many similarities and a few differences between the two models: | There are many similarities and a few differences between the two models: | ||
| Line 211: | Line 211: | ||
$\text{Example 2:}$ The figure above shows an exemplary error sequence of the GE model with the parameters $p_{\rm G} = 0.01$, $p_{\rm B} = 0.4$, ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01$, ${\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1$. It can be seen that, in contrast to the lower MC sequence, a change of state from "GOOD" (without background) to "BAD" (gray background) and vice versa is possible at any time $\nu$ – i.e. even when $e_\nu = 0$. <br> | $\text{Example 2:}$ The figure above shows an exemplary error sequence of the GE model with the parameters $p_{\rm G} = 0.01$, $p_{\rm B} = 0.4$, ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01$, ${\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1$. It can be seen that, in contrast to the lower MC sequence, a change of state from "GOOD" (without background) to "BAD" (gray background) and vice versa is possible at any time $\nu$ – i.e. even when $e_\nu = 0$. <br> | ||
| − | [[File: | + | [[File:EN_Dig_T_5_3_S4.png|center|frame|Error sequence of the GE model (top) and the MC model (bottom)|class=fit]]}} |
| Line 334: | Line 334: | ||
$\text{Example 5:}$ We consider a block with $n$ bits, starting at bit position $\nu + 1$. | $\text{Example 5:}$ We consider a block with $n$ bits, starting at bit position $\nu + 1$. | ||
| − | [[File: | + | [[File:EN_Dig_T_5_3_S5c.png|right|frame|To derive the Wilhelm model|class=fit]] |
*A block error occurs whenever a bit is falsified at positions $\nu + 1$, ... , $\nu + n$. <br> | *A block error occurs whenever a bit is falsified at positions $\nu + 1$, ... , $\nu + n$. <br> | ||
| Line 479: | Line 479: | ||
Nun vergleichen wir die Unterschiede der beiden Wilhelm–Modelle ('''L''' bzw. '''A''') hinsichtlich resultierender Blockfehlerwahrscheinlichkeit. | Nun vergleichen wir die Unterschiede der beiden Wilhelm–Modelle ('''L''' bzw. '''A''') hinsichtlich resultierender Blockfehlerwahrscheinlichkeit. | ||
| − | [[File: | + | [[File:EN_Dig_T_5_3_S5korr_version2.png|right|frame||Ergebnisse des Wilhelm–Modells für $p_{\rm S} = 0.01$ und einige $\alpha$ ]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 8:}$ Nebenstehende Grafik zeigt den Verlauf der Blockfehlerwahrscheinlichkeiten $p_{\rm B}(n)$ für drei verschiedene $\alpha$–Werte, erkennbar an den Farben | $\text{Beispiel 8:}$ Nebenstehende Grafik zeigt den Verlauf der Blockfehlerwahrscheinlichkeiten $p_{\rm B}(n)$ für drei verschiedene $\alpha$–Werte, erkennbar an den Farben | ||
| Line 529: | Line 529: | ||
Nachfolgend werden die Eigenschaften der Fehlerkorrelationsfunktion an einem Beispiel aufgezeigt.<br> | Nachfolgend werden die Eigenschaften der Fehlerkorrelationsfunktion an einem Beispiel aufgezeigt.<br> | ||
| − | [[File: | + | [[File:EN_Dig_T_5_3_S5korr_version2.png|right|frame||Fehlerkorrelationsfunktionen des Wilhelm–Modells]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 9:}$ | $\text{Beispiel 9:}$ | ||
Revision as of 16:51, 1 September 2022
Contents
- 1 Channel model according to Gilbert-Elliott
- 2 Error distance distribution of the GE model
- 3 Error correlation function of the GE model
- 4 Channel model according to McCullough
- 5 Conversion of the GE parameters into the MC parameters
- 6 Burst error channel model according to Wilhelm
- 7 Error distance consideration to the Wilhelm model
- 8 Numerical comparison of the BSC model and the Wilhelm model
- 9 Fehlerabstandsbetrachtung nach dem Wilhelm–A–Modell
- 10 Fehlerkorrelationsfunktion des Wilhelm–A–Modells
- 11 Analyse von Fehlerstrukturen mit dem Wilhelm–A–Modell
- 12 Aufgaben zum Kapitel
- 13 Quellenverzeichnis
Channel model according to Gilbert-Elliott
This channel model, which goes back to "E. N. Gilbert" [Gil60][1] and E. O. Elliott [Ell63][2], is suitable for describing and simulating digital transmission systems with burst error characteristics.
The Gilbert–Elliott model (abbreviation: GE model) can be characterized as follows:
- The different transmission quality at different times is expressed by a finite number $g$ of channel states $(Z_1, Z_2,\hspace{0.05cm} \text{...} \hspace{0.05cm}, Z_g)$.
- The in reality smooth transitions of the noise intensity – in the extreme case from completely error-free transmission to total failure – are approximated in the GE model by fixed probabilities in the individual channel states.
- The transitions between the $g$ states occur according to a "Markov process" (1st order) and are characterized by $g \cdot (g-1)$ transition probabilities. Together with the $g$ error probabilities in the individual states, there are thus $g^2$ free model parameters.
- For reasons of mathematical manageability, one usually restricts oneself to $g = 2$ states and denotes these with $\rm G$ ("GOOD") and $\rm B$ ("BAD"). Mostly, the error probability in state $\rm G$ will be much smaller than in state $\rm B$.
- In what follows, we use these two error probabilities $p_{\rm G}$ and $p_{\rm B}$, where $p_{\rm G} < p_{\rm B}$ should hold, as well as the transition probabilities ${\rm Pr}({\rm B}\hspace{0.05cm}|\hspace{0.05cm}{\rm G})$ and ${\rm Pr}({\rm G}\hspace{0.05cm}|\hspace{0.05cm}{\rm B})$. This also determines the other two transition probabilities:
- \[{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) = 1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G), \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B) = 1 - {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{0.05cm}.\]
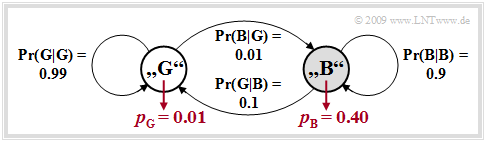
$\text{Example 1:}$ We consider the GE model with the parameters
- $$p_{\rm G} = 0.01,$$
- $$p_{\rm B} = 0.4,$$
- $${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) = 0.1, $$
- $$ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
The underlying model is shown at the end of the example with the parameters given here.
The upper graphic shows a (possible) error sequence of length $N = 800$. If the GE model is in the "BAD" state, this is indicated by the gray background.
To simulate such a GE error sequence, switching is performed between the states "GOOD" and "BAD" according to the four transition probabilities.
- At the first clock call, the selection of the state is expediently done according to the probabilities $w_{\rm G}$ and $w_{\rm B}$, as calculated below.
- At each clock cycle exactly one element of the error sequence $ \langle e_\nu \rangle$ is generated according to the current error probability $(p_{\rm G}$ or $p_{\rm B})$.
- The "error distance simulation" is not applicable here, because in the GE model a state change is possible after each symbol (and not only after an error).
The probabilities that the Markov chain is in the "GOOD" or "BAD" state can be calculated from the assumed homogeneity and stationarity. One obtains with the above numerical values:
- \[w_{\rm G} = {\rm Pr(in\hspace{0.15cm} state \hspace{0.15cm}G)}= \frac{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B)}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01} = {10}/{11}\hspace{0.05cm},\]
- \[w_{\rm B} = {\rm Pr(in\hspace{0.15cm} state \hspace{0.15cm}B)}= \frac{ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)} = \frac{0.11}{0.1 + 0.01} = {1}/{11}\hspace{0.05cm}.\]
These two state probabilities can also be used to determine the average error probability of the GE model:
- \[p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \frac{p_{\rm G} \cdot {\rm Pr}({\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B)}+ p_{\rm B} \cdot {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)} \hspace{0.05cm}.\]
In particular, for the model considered here as an example:
- \[p_{\rm M} ={10}/{11} \cdot 0.01 +{1}/{11} \cdot 0.4 = {1}/{22} \approx 4.55\%\hspace{0.05cm}.\]
Error distance distribution of the GE model
In [Hub82][3] you can find the analytical computations
- of the probability of the error distance $k$:
- \[{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm G}) + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm B})\hspace{0.05cm},\]
- \[V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.\]
The following auxiliary quantities are used here:
- \[u_{\rm GG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\]
- \[u_{\rm BB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}\]
- \[\Rightarrow \hspace{0.3cm} \beta_{\rm G} =\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},\]
- \[\hspace{0.8cm}\beta_{\rm B} =\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]
- \[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}\]
- \[\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]
The given equations are the result of extensive matrix operations.
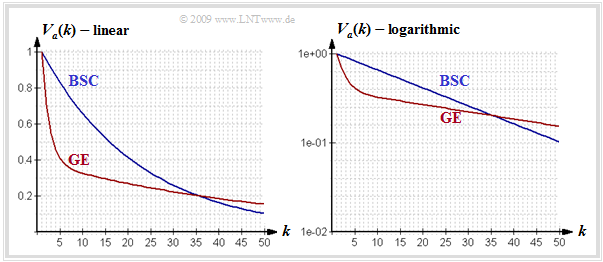
The upper graph shows the error distance distribution (EDD) of the GE model (red curve) in linear and logarithmic representation for the parameters
- $${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = 0.1 \hspace{0.05cm},\hspace{0.5cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) = 0.001 \hspace{0.05cm},\hspace{0.5cm}p_{\rm B} = 0.4.$$
For comparison, the corresponding $V_a(k)$ curve for the BSC model with the same mean error probability $p_{\rm M} = 4.5\%$ is also plotted as a blue curve.
Error correlation function of the GE model
For the "error correlation function" (ECF) of the GE model with
- the mean error probability $p_{\rm M}$,
- the transition probabilities ${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )$ and ${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )$ as well as
- the error probabilities $p_{\rm G}$ and $p_{\rm B}$ in the two states $\rm G$ and $\rm B$
we obtain after extensive matrix operations the relatively simple expression
- \[\varphi_{e}(k) = {\rm E}\big[e_\nu \cdot e_{\nu +k}\big] = \left\{ \begin{array}{c} p_{\rm M} \\ p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) (p_{\rm M} - p_{\rm G}) [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^k \end{array} \right.\quad \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}\]
For the GE model, $\varphi_{e}(k)$ must always be calculated according to this equation. The iterative calculation algorithm
- $$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa) $$
which is only valid for "renewing models", cannot be applied here, since the GE model is not renewing ⇒ The error distances are not statistically independent of each other here.
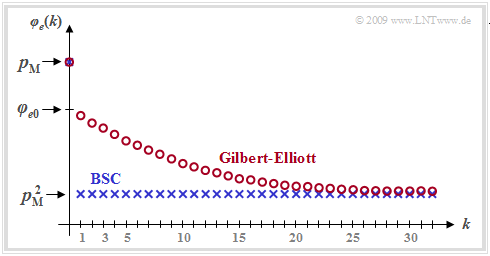
The graph shows an example of the ECF curve of the GE model marked with red circles. One can see from this representation:
- While for the memoryless channel (BSC model, blue curve) all ECF values are $\varphi_{e}(k \ne 0)= p_{\rm M}^2$ for the burst error channel the ECF values approach this final value much more slowly.
- At the transition from $k = 0$ to $k = 1$ a certain discontinuity occurs. While $\varphi_{e}(k = 0)= p_{\rm M}$, the second equation valid for $k > 0$ yields the following extrapolated value for $k = 0$:
- \[\varphi_{e0} = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G})\hspace{0.05cm}.\]
- A quantitative measure of the length of the statistical ties is the correlation duration $D_{\rm K}$, which is generally defined as the width of an equal-area rectangle of height $\varphi_{e0} - p_{\rm M}^2$:
- \[D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} \big[\varphi_{e}(k) - p_{\rm M}^2\big ]\hspace{0.05cm}.\]
$\text{Conclusion:}$ In the Gilbert–Elliott model, the correlation term is given by the simple, analytically expressible expression
- \[D_{\rm K} =\frac{1}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G )}-1 \hspace{0.05cm}.\]
- $D_{\rm K}$ is larger the smaller ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G )$ and ${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ are, i.e., when state changes occur rarely.
- For the BSC model ⇒ $p_{\rm B}= p_{\rm G} = p_{\rm M}$ ⇒ $D_{\rm K} = 0$ this equation is not applicable.
Channel model according to McCullough
The main disadvantage of the GE model is that it does not allow error distance simulation. As will be worked out in "Exercise 5.5", this has great advantages over the symbol-wise generation of the error sequence $\langle e_\nu \rangle$ in terms of computational speed and memory requirements.
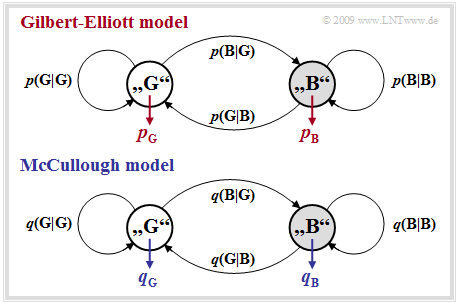
McCullough [McC68][4] modified the model developed three years earlier by Gilbert and Elliott so that an error distance simulation in the two states "GOOD" and "BAD" is applicable in each case by itself. The graph below shows McCullough's model, hereafter referred to as the MC model, while the GE model is shown above after renaming the transition probabilities ⇒ ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, etc.
There are many similarities and a few differences between the two models:
- Like the Gilbert–Elliott model, the McCullough channel model is based on a first-order Markov process with the two states "GOOD" $(\rm G)$ and "BAD" $(\rm B)$. No difference can be found with respect to the model structure.
- The main difference to the GE model is that a change of state between "GOOD" and "BAD" is only possible after an error – i.e. a "$1$" in the error sequence. This enables a error distance simulation.
- The four freely selectable GE parameters $p_{\rm G}$, $p_{\rm B}$, ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ and ${\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ can – as shown on the next section – be converted into the MC parameters $q_{\rm G}$, $q_{\rm B}$, ${\it q}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ and ${\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ in such a way that a error sequence with the same statistical properties as in the GE model is generated.
- For example, ${\it q}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ denotes the transition probability from the "GOOD" state to the "BAD" state under the condition that an error has just occurred in the "GOOD" state. The GE parameter ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ characterizes this transition probability without this additional condition.
$\text{Example 2:}$ The figure above shows an exemplary error sequence of the GE model with the parameters $p_{\rm G} = 0.01$, $p_{\rm B} = 0.4$, ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01$, ${\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1$. It can be seen that, in contrast to the lower MC sequence, a change of state from "GOOD" (without background) to "BAD" (gray background) and vice versa is possible at any time $\nu$ – i.e. even when $e_\nu = 0$.
$\text{Conclusion:}$ The correlations between the two models can be summarized as follows:
- In the error sequence of the McCullough model shown in the example below, in contrast to the upper sequence, a change of state at time $\nu$ is only possible at $e_\nu = 1$. The last error value before a gray background is always a "$1$".
- This has the advantage that one does not have to generate the errors "step–by–step" in an error sequence simulation, but can use the faster error distance simulation ⇒ see "Exercise 5.5".
- The parameters of the GE model can be converted into corresponding MC parameters in such a way that the two models are equivalent ⇒ see next section. That means: The MC error sequence has exactly the same statistical properties as the GE error sequence. However, it does not mean that both error sequences are identical.
Conversion of the GE parameters into the MC parameters
The parameters of the equivalent MC model can be calculated from the GE parameters as follows:
- \[q_{\rm G} =1-\beta_{\rm G}\hspace{0.05cm}, \hspace{0.9cm}q_{\rm B} = 1-\beta_{\rm B}\hspace{0.05cm}, \hspace{0.9cm}q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) =\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm}, \hspace{0.9cm} q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.\]
Here again the following auxiliary quantities are used:
- \[u_{\rm GG} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\]
- \[u_{\rm BB} = {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\]
- \[\Rightarrow \hspace{0.3cm} \beta_{\rm G} = \frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm}, \hspace{0.9cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]
- \[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}} \Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.9cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]
$\text{Example 3:}$ As in $\text{Example 2}$, the GE parameters are:
- $$p_{\rm G} = 0.01, \hspace{0.5cm} p_{\rm B} = 0.4, \hspace{0.5cm} p(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01, \hspace{0.5cm} {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1.$$
Applying the above equations, we then obtain for the equivalent MC parameters:
- $$q_{\rm G} = 0.0186, \hspace{0.5cm} q_{\rm B} = 0.4613, \hspace{0.5cm} q(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.3602, \hspace{0.5cm} {\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.2240.$$
- If we compare in $\text{Example 2}$ the red error sequence (GE, change of state is always possible) with the blue sequence (equivalent MC, change of state only at $e_\nu = 1$), we can see quite serious differences.
- But the blue error sequence of the equivalent McCullough model has exactly the same statistical properties as the red error sequence of the Gilbert-Elliott model.
The conversion of the GE parameters to the MC parameters is illustrated in "Exercise 5.7" using a simple example. "Exercise 5.7Z" further shows how the mean error probability, the error distance distribution, the error correlation function and the correlation duration of the MC model can be determined directly from the $q$ parameters.
Burst error channel model according to Wilhelm
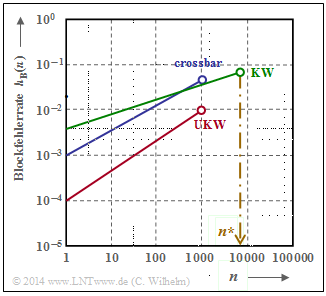
This model goes back to "Claus Wilhelm" and was developed from the mid-1960s onwards from empirical measurements of temporal consequences of bit errors. It is based on thousands of measurement hours in transmission channels from $\text{200 bit/s}$ with analog modem up to $\text{2.048 Mbit/s}$ via "ISDN". Likewise, marine radio channels up to $7500$ kilometers in the shortwave range were measured.
Blocks of length $n$ were recorded. The respective block error rate $h_{\rm B}(n)$ was determined from this.
- A block error is already present if even one of the $n$ symbols has been falsified.
- Knowing well that the block error rate $h_{\rm B}(n)$ corresponds exactly to the block error probability $p_{\rm B}$ only for $n \to \infty$, we set $p_{\rm B}(n) \approx h_{\rm B}(n)$ in the following description.
In a large number of measurements, the fact that the course $p_{\rm B}(n)$ in double-logarithmic representation show linear increases in the lower range has been confirmed again and again (see graph). Thus, it holds for $n \le n^\star$:
- \[{\rm lg} \hspace{0.15cm}p_{\rm B}(n) = {\rm lg} \hspace{0.15cm}p_{\rm S} + \alpha \cdot {\rm lg} \hspace{0.15cm}n\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\hspace{0.05cm}.\]
Here, $p_{\rm S} = p_{\rm B}(n=1)$ denotes the mean symbol error probability and the empirically found values of $\alpha$ are between $0.5$ and $0.95$. For $1-\alpha$, the term burst factor is also used.
Note that $p_{\rm B}(n)$ indicates the block error probability. In another context, $p_{\rm B}$ sometimes also denotes the bit error probability in our learning tutorial.
$\text{Example 4:}$ In the BSC model, the course of the block error probability is:
- \[p_{\rm B}(n) =1 -(1 -p_{\rm S})^n \approx n \cdot p_{\rm S}\hspace{0.05cm}.\]
From this follows $\alpha = 1$ resp. the burst factor $1-\alpha = 0$. In this case (and only in this case) a linear course results even with non-logarithmic representation.
- Note that the above approximation is only valid for $p_{\rm S} \ll 1$ and not too large $n$, otherwise the approximation $(1-p_{\rm S})^n \approx1 - n \cdot p_{\rm S}$ is not applicable.
- But this also means that the equation given above is also only valid for a lower range $($for $n < n^\star)$.
- Otherwise, an infinitely large block error probability would result for $n \to \infty$.
$\text{Definition:}$ For the function $p_{\rm B}(n)$ determined empirically from measurements, we now have to find the error distance distribution from which the course for $n > n^\star$ can be extrapolated, which satisfies the following constraint:
- \[\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_{\rm B}(n) = 1 .\]
We refer to this approach as the Wilhelm model. Since memory extends only to the last symbol error, this model is renewal model..
Error distance consideration to the Wilhelm model
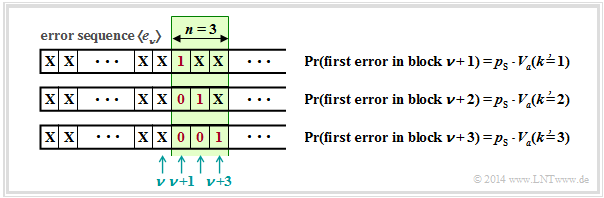
We now consider the error distances. An error sequence $\langle e_\nu \rangle$ can be equivalently represented by the error distance sequence $\langle a_{\nu\hspace{0.06cm}'} \rangle$, as shown in the following graph. It can be seen:
- The error sequence $\text{...}\rm 1001\text{...}$ is expressed by $a= 3$.
- Accordingly, the error distance $a= 1$ denotes the error sequence $\text{...}\rm 11\text{...}$.
- The different indices $\nu$ and $\nu\hspace{0.06cm}'$ take into account that the two sequences do not run synchronously.
With the probabilities $p_a(k) = {\rm Pr}(a= k)$ for the individual error distances $k$ and the mean (symbol) error probability $p_{\rm S}$, the following definitions apply for
- the error distance distribution (EDD):
- \[ V_a(k) = {\rm Pr}(a \ge k)= \sum_{\kappa = k}^{\infty}p_a(\kappa) \hspace{0.05cm},\]
- the mean error distance ${\rm E}\big[a\big]$:
- \[ V_a(k) = {\rm E}\big[a\big] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = {1}/{p_{\rm S}}\hspace{0.05cm}.\]
$\text{Example 5:}$ We consider a block with $n$ bits, starting at bit position $\nu + 1$.
- A block error occurs whenever a bit is falsified at positions $\nu + 1$, ... , $\nu + n$.
- The falsification probabilities are expressed in the graph by the error distance distribution ${V_a}\hspace{0.06cm}'(k)$.
- Somewhere before the block of length $n = 3$ is the last error, but at least at distance $k$ from the first error in the block.
- So the distance is equal or greater than $k$, which corresponds exactly to the probability ${V_a}'(k)$.
- The apostrophe is to indicate that a correction has to be made later to get from the empirically found EDD to the correct function ${V_a}(k)$.
We now have several equations for the block error probability $p_{\rm B}(n)$.
- A first equation establishes the relationship between $p_{\rm B}(n)$ and the (approximate) error distance distribution ${V_a}'(k)$:
- \[(1)\hspace{0.4cm} p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) \hspace{0.05cm}, \]
- A second equation is provided by our empirical investigation at the beginning of this section:
- \[(2)\hspace{0.4cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\]
- The third equation is obtained by equating $(1)$ and $(2)$:
- \[(3)\hspace{0.4cm} \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) = n^{\alpha} \hspace{0.05cm}. \]
By successively substituting $n = 1, 2, 3,$ ... into this equation, we obtain with ${V_a}'(k = 1) = 1$:
- \[V_a\hspace{0.05cm}'(1) = 1^{\alpha} \hspace{0.05cm},\hspace{0.8cm} V_a\hspace{0.05cm}'(1) + V_a\hspace{0.05cm}'(2) =2^{\alpha} \hspace{0.05cm}, \hspace{0.8cm}V_a\hspace{0.05cm}'(1) + V_a\hspace{0.05cm}'(2) + V_a\hspace{0.05cm}'(3) = 3^{\alpha} \hspace{0.35cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}'(k) = k^{\alpha}-(k-1)^{\alpha} \hspace{0.05cm}.\]
However, the coefficients ${V_a}'(k)$ obtained from empirical data do not necessarily satisfy the normalization condition.
To correct the issue, Wilhelm uses the following approach:
- \[V_a\hspace{0.05cm}(k) = V_a\hspace{0.05cm}'(k) \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.05cm}.\]
Wilhelm refers to this representation as the L–model, see [Wil11][5]. The constant $\beta$ is dependent on
- the symbol error probability $p_{\rm S}$, and
- the empirically found exponent $\alpha$ ⇒ burst factor $1- \alpha$
such that the block error probability becomes equal to $1$ at infinite block length:
- \[\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_B(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) = p_{\rm S} \cdot \sum_{k = 1}^{n} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sum_{k = 1}^{\infty} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} = {1}/{p_{\rm S}} \hspace{0.05cm}.\]
To determine $\beta$, we use the "generating function" of ${V_a}(k)$, which we denote by ${V_a}(z)$:
- \[V_a\hspace{0.05cm}(z) = \sum_{k = 1}^{\infty}V_a\hspace{0.05cm}(k) \cdot z^k = \sum_{k = 1}^{n} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} \cdot z^k \hspace{0.05cm}.\]
In [Wil11][5], $V_a\hspace{0.05cm}(z) = 1/{\left (1- {\rm e}^{- \beta }\cdot z \right )^\alpha} $ is derived approximately. From the equation for the mean error distance follows:
- \[ {\rm E}\big[a\big] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = \sum_{k = 1}^{\infty} V_a(k) = \sum_{k = 1}^{\infty} V_a(k) \cdot 1^k = V_a(z=1) = 1/p_{\rm S}\]
- \[ \Rightarrow \hspace{0.3cm}{p_{\rm S}} = \big [V_a(z=1)\big]^{-1}= \big [1- {\rm e}^{- \beta }\cdot 1\big]^{\alpha}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm e}^{- \beta } =1 - {p_{\rm S}}^{1/\alpha}\hspace{0.05cm}.\]
Numerical comparison of the BSC model and the Wilhelm model
$\text{Conclusion:}$ Let us summarize this intermediate result. Wilhelm's L–model describes the error distance distribution in the form
- \[V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha}\big ] \cdot \big [ 1 - {p_{\rm S}^{1/\alpha} }\big ]^{k-1} \hspace{0.05cm}.\]
This model will now be explained with exemplary numerical results.
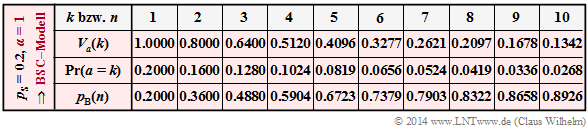
$\text{Example 6:}$ We start with the "BSC model".
- For presentation reasons, we set the falsification probability very high to $p_{\rm S} = 0.2$.
- In the second row of the following table, its error distance distribution ${V_a}(k) = {\rm Pr}(a \ge k)$ is entered for $k \le10$.
The Wilhelm model with $p_{\rm S} = 0.2$ and $\alpha = 1$ has exactly the same error distance distribution ${V_a}(k)$ as the corresponding "BSC model". This is also shown by the calculation. Mit $\alpha = 1$ erhält man aus der Gleichung auf der letzten Seite:
- \[V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha}\big ] \cdot \big [ 1 - {p_{\rm S}^{1/\alpha} }\big ]^{k-1} = (1 - p_{\rm S} )^{k-1} \hspace{0.05cm}.\]
Damit besitzen beide Modelle entsprechend den Zeilen 3 und 4 auch
- gleiche Wahrscheinlichkeiten ${\rm Pr}(a = k)= {V_a}(k-1) - {V_a}(k)$ der Fehlerabstände,
- gleiche Blockfehlerwahrscheinlichkeiten $ p_{\rm B}(n)$.
Im Hinblick auf das folgende $\text{Beispiel 7}$ mit $\alpha \ne 1$ ist nochmals besonders zu erwähnen:
- Die Blockfehlerwahrscheinlichkeiten $ p_{\rm B}(n)$ des Wilhelm–Modells ergeben sich grundsätzlich aus der Fehlerabstandsverteilung ${V_a}(k)$ entsprechend der Gleichung
- \[ p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} p_{\rm B}( 1) = 0.2 \cdot 1 = 0.2 \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B}(2) = 0.2 \cdot (1+0.8) = 0.36 \hspace{0.05cm}.\]
- Nur im Sonderfall $\alpha = 1$ ⇒ BSC–Modell kann $ p_{\rm B}(n)$ auch durch Summation über die Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a=k)$ ermittelt werden:
- \[ p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} {\rm Pr}(a=k) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} p_{\rm B}( 1) = 0.2 \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B}(2) = 0.2+ 0.16 = 0.36 \hspace{0.05cm}.\]
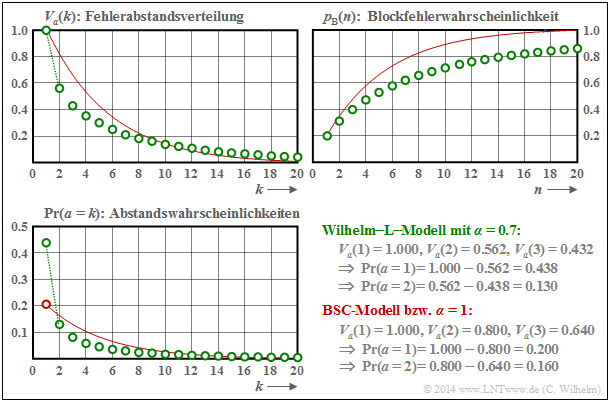
$\text{Beispiel 7:}$ Wir betrachten nun einen Kanal mit Bündelfehlercharakteristik.
- Die Grafik zeigt als grüne Kreise die Ergebnisse für das Wilhelm–L–Modell mit $\alpha = 0.7$.
- Die rote Vergleichskurve gilt für $\alpha = 1$ (bzw. für den BSC–Kanal) bei gleicher mittlerer Symbolfehlerwahrscheinlichkeit $p_{\rm S} = 0.2$.
- Unten rechts sind einige interessante Zahlenwerte angegeben.
Man erkennt aus diesen Darstellungen:
- Der Verlauf der Blockfehlerfehlerwahrscheinlichkeit beginnt jeweils mit $p_{\rm B}(n = 1) = p_{\rm S} = 0.2$, sowohl bei statistisch unabhängigen Fehlern (BSC) als auch bei Bündelfehlern (Wilhelm).
- Beim Bündelfehlerkanal ist ${\rm Pr}(a=1)= 0.438$ deutlich größer als beim vergleichbaren BSC ⇒ ${\rm Pr}(a=1)= 0.2$. Zudem erkennt man einen abgeknickten Verlauf im unteren Bereich.
- Der mittlere Fehlerabstand ${\rm E}\big [a \big ] = 1/p_{\rm S} = 5$ ist aber bei gleicher Symbolfehlerwahrscheinlichkeit ebenfalls identisch. Der große Ausreiser bei $k=1$ wird durch kleinere Wahrscheinlichkeiten für $k=2$, $k=3$ ... ausgeglichen, sowie durch die Tatsache, dass für große $k$ die grünen Kreise – wenn auch nur minimal – oberhalb der roten Vergleichskurve liegen.
- Das wichtigste Ergebnis ist aber, dass die Blockfehlerfehlerwahrscheinlichkeit für $n > 1$ beim Bündelfehlerkanal kleiner ist als beim vergleichbaren BSC–Modell, zum Beispiel: $p_{\rm B}(n = 20) = 0.859$.
Fehlerabstandsbetrachtung nach dem Wilhelm–A–Modell
Wilhelm hat aus der oben angegebenen erzeugenden Funktion $V_a(z)$ eine weitere Näherung entwickelt, die er als das A–Modell bezeichnet. Die Näherung basiert auf einer Taylorreihenentwicklung.
$\text{Definition:}$ Das A–Modell nach Wilhelm beschreibt die angenäherte Fehlerabstandsverteilung in der Form
- \[V_a\hspace{0.05cm}(k) = \frac {1 \cdot \alpha \cdot (1+\alpha) \cdot \hspace{0.05cm} ... \hspace{0.05cm}\cdot (k-2+\alpha) }{(k-1)\hspace{0.05cm}!}\cdot \left [ 1 - {p_{\rm S}^{1/\alpha} }\right ]^{k-1} \hspace{0.05cm}.\]
- Insbesondere ergibt sich $V_a(k = 1) = 1$ und $V_a(k = 2)= \alpha \cdot (1 - p_{\rm S}^{1/\alpha})$.
- Hierbei ist zu berücksichtigen, dass der Zähler des Vorfaktors aus $k$ Faktoren besteht. Für $k = 1$ ergibt sich dieser Vorfaktor demzufolge zu $1$.
Nun vergleichen wir die Unterschiede der beiden Wilhelm–Modelle (L bzw. A) hinsichtlich resultierender Blockfehlerwahrscheinlichkeit.
$\text{Beispiel 8:}$ Nebenstehende Grafik zeigt den Verlauf der Blockfehlerwahrscheinlichkeiten $p_{\rm B}(n)$ für drei verschiedene $\alpha$–Werte, erkennbar an den Farben
- Rot: $\alpha = 1$ ⇒ BSC–Modell,
- Blau: $\alpha = 0.95$ ⇒ schwache Bündelung,
- Grün: $\alpha = 0.7$ ⇒ starke Bündelung.
Die durchgezogenen Linien gelten für das A–Modell und die gestrichelten für das L–Modell. Die im Bild angegebenen Zahlenwerte für $p_{\rm B}(n = 100)$ beziehen sich ebenfalls auf das A–Modell.
Für $\alpha = 1$ geht sowohl das A–Modell als auch das L–Modell in das BSC–Modell (rote Kurve) über.
Desweiteren ist anzumerken:
- Die Symbolfehlerwahrscheinlichkeit $p_{\rm S} = 0.01$ ⇒ ${\rm E}\big[a \big ] = 100$ ist hier (einigermaßen) realistisch angenommen. Alle Kurven starten so bei $p_{\rm B}(n=1) = 0.01$ ⇒ gelber Punkt.
- Der Unterschied zwischen zwei gleichfarbigen Kurven ist gering (bei starker Bündelung etwas größer), wobei die durchgezogene Kurve stets oberhalb der gestrichelten Kurve liegt.
- Auch dieses Beispiel zeigt: Je stärker die Bündelung $($kleineres $\alpha)$, desto kleiner ist die Blockfehlerwahrscheinlichkeit $p_{\rm B}(n)$. Dies gilt allerdings nur, wenn man wie hier von einer konstanten Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ausgeht.
- Ein (dürftiger) Erklärungsversuch: Nehmen wir an, dass bei BSC mit sehr kleinem $p_{\rm S}$ jeder Blockfehler von genau einem Symbolfehler herrührt, dann gibt es bei gleicher Symbolfehleranzahl weniger Blockfehler, wenn zwei Symbolfehler in einen Block fallen (Bündelung).
- Noch ein (passenderes?) Beispiel aus dem täglichen Leben. Man kann eine Straße bei konstantem Verkehrsaufkommen leichter überqueren, wenn die Fahrzeuge "irgendwie gebündelt" kommen.
Fehlerkorrelationsfunktion des Wilhelm–A–Modells
Eine weitere Beschreibungsform der digitalen Kanalmodelle ist neben der Fehlerabstandsverteilung $V_a(k)$ die Fehlerkorrelationsfunktion $\varphi_{e}(k)$ – abgekürzt FKF. Wir gehen von der binären Fehlerfolge $\langle e_\nu \rangle$ mit $e_\nu \in \{0, 1\}$ aus, wobei hinsichtlich des $\nu$–ten Bits
- $e_\nu = 0$ eine richtige Übertragung bezeichnet, und
- $e_\nu = 1$ einen Symbolfehler (Bitfehler).
$\text{Definition:}$ Die Fehlerkorrelationsfunktion $\varphi_{e}(k)$ gibt die (zeitdiskrete) Autokorrelationsfunktion der ebenfalls zeitdiskreten Zufallsgröße $e$ an.
- \[\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]
Die überstreichende Linie in der rechten Gleichung kennzeichnet die Zeitmittelung.
Der Fehlerkorrelationswert $\varphi_{e}(k)$ liefert statistische Aussagen bezüglich zwei um $k$ auseinander liegender Folgenelemente, zum Beispiel über $e_{\nu}$ und $e_{\nu +k}$. Die dazwischen liegenden Elemente $e_{\nu +1}$, ... , $e_{\nu +k-1}$ beeinflussen dagegen den $\varphi_{e}(k)$–Wert nicht.
$\text{Ohne Beweis:}$ Die Fehlerkorrelationsfunktion des Wilhelm–A–Modells kann wie folgt angenähert werden:
\[\varphi_e\hspace{0.05cm}(k) = p_{\rm S} \hspace{-0.03cm}\cdot \hspace{-0.03cm} \left [ 1 \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha}{1\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha \cdot (1\hspace{-0.03cm}-\hspace{-0.03cm} \alpha)}{2\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^2 \hspace{-0.03cm}-\hspace{-0.03cm} \hspace{0.05cm} \text{...} \hspace{0.05cm}\hspace{-0.03cm}-\hspace{-0.03cm} \frac {\alpha \hspace{-0.03cm}\cdot \hspace{-0.03cm} (1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) \hspace{-0.03cm}\cdot \hspace{-0.03cm} \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{-0.03cm}\cdot \hspace{-0.03cm} (k\hspace{-0.03cm}-\hspace{-0.03cm}1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) }{k\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^k \right ] \]
Zur Abkürzung ist $C = (1-p_{\rm S})^{1/\alpha}$ verwendet. Auf die Herleitung wird hier verzichtet.
Nachfolgend werden die Eigenschaften der Fehlerkorrelationsfunktion an einem Beispiel aufgezeigt.
$\text{Beispiel 9:}$ Wie im $\text{Beispiel 8}$ gelte $p_{\rm S} = 0.01$. Die hier dargestellten Fehlerkorrelationsfunktionen stehen wieder für
- Grün: $\alpha = 0.7$ ⇒ starke Bündelung.
- Blau: $\alpha = 0.95$ ⇒ schwache Bündelung,
- Rot: $\alpha = 1$ ⇒ BSC–Modell,
Die folgenden Aussagen lassen sich weitgehend verallgemeinern, siehe auch GE–Modell:
- Der FKF-Wert an der Stelle $k = 0$ ist bei allen Kanälen gleich $p_{\rm S} = 10^{-2}$ (markiert durch den Kreis mit grauer Füllung) und der Grenzwert für $k \to \infty$ liegt stets bei $p_{\rm S}^2 = 10^{-4}$.
- Dieser Endwert wird beim BSC–Modell bereits bei $k = 1$ erreicht (rot gefüllte Markierung). Hier kann die FKF also nur die beiden Werte $p_{\rm S}$ und $p_{\rm S}^2$ annehmen.
- Auch für für $\alpha < 1$ (blaue und grüne Kurve) erkennt man einen Knick bei $k = 1$. Danach verläuft die FKF monoton fallend. Der Abfall ist umso langsamer, je kleiner $\alpha$ ist, also je gebündelter die Fehler auftreten.
Analyse von Fehlerstrukturen mit dem Wilhelm–A–Modell
Wilhelm hat sein Kanalmodell hauptsächlich deshalb entwickelt, um aus gemessenen Fehlerfolgen Rückschlüsse über die dabei auftretenden Fehler machen zu können. Aus der Vielzahl der Analysen in [Wil11][5] sollen hier nur einige wenige angeführt werden, wobei stets die Symbolfehlerwahrscheinlichkeit $p_{\rm S} = 10^{-3}$ zugrunde liegt.
- In den Grafiken gilt jeweils die rote Kurve für statistisch unabhängige Fehler $($BSC bzw. $\alpha = 1)$,
- die grüne Kurve für einen Bündelfehlerkanal mit $\alpha = 0.7$. Zudem soll folgende Vereinbarung gelten:
$\text{Definition:}$ Ein Fehlerburst (oder kurz Burst) beginnt stets mit einem Symbolfehler und endet, wenn $k_{\rm Burst}- 1$ fehlerfreie Symbole aufeinanderfolgen.
- $k_{\rm Burst}$ bezeichnet den Burst–Endeparameter.
- Das Burstgewicht $G_{\rm Burst}$ entspricht der Anzahl aller Symbolfehler im Burst.
- Bei einem Einzelfehler gilt $G_{\rm Burst}= 1$ und die Burstlänge (bestimmt durch den ersten und letzten Fehler) ist ebenfalls $L_{\rm Burst}= 1$.
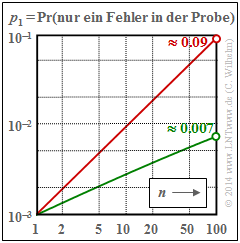
$\text{Beispiel 10:}\ \text{Wahrscheinlichkeit }p_1\text{ eines Einzelfehlers in einer Probe der Länge} \ n$
Für den BSC–Kanal $(\alpha = 1)$ gilt $p_1 = n \cdot 0.001 \cdot 0.999^{n-1}$ ⇒ rote Kurve. Aufgrund der doppel–logarithmischen Darstellung ergibt sich mit diesen Zahlenwerten ein (nahezu) linearer Verlauf. Beim BSC–Modell treten also Einzelfehler in einer Probe der Länge $n = 100$ mit etwa $9\%$ Wahrscheinlichkeit auf.
Beim Bündelfehlerkanal mit $\alpha = 0.7$ (grüne Kurve) beträgt die entsprechende Wahrscheinlichkeit nur etwa $0.7\%$ und der Kurvenverlauf ist hier leicht gekrümmt.
Bei der folgenden Rechnung gehen wir zunächst von der Annahme aus, dass der Einzelfehler in der Probe der Länge $n$ an der Position $b$ auftritt:
- Bei einem Einzelfehler müssen dann noch $n-b$ fehlerfreie Symbole folgen. Nach Mittelung über die möglichen Fehlerpositionen $b$ erhält man somit:
- \[p_1 = p_{\rm S} \cdot \sum_{b = 1}^{n} \hspace{0.15cm}V_a (b) \cdot V_a (n+1-b) \hspace{0.05cm}.\]
- Wegen der Ähnlichkeit mit der Signaldarstellung eines Digitalen Filters kann man die Summe als Faltung von $V_a(b)$ mit sich selbst bezeichnen. Für die erzeugende Funktion $V_a(z)$ wird aus der Faltung ein Produkt (bzw. wegen $V_a(b) \star V_a(b)$ das Quadrat) und man erhält folgende Gleichung:
- \[V_a(z=1) \cdot V_a(z=1) = \big [ V_a(z=1) \big ]^2 = {\big [ 1 -(1- {p_{\rm S} }^{1/\alpha})\big ]^{-2\alpha} } \hspace{0.05cm}.\]
- Mit der spezifischen Fehlerabstandsverteilung $V_a(z)$ erhält man somit folgendes Endergebnis:
- \[p_1 = p_{\rm S} \cdot \frac{2\alpha \cdot (2\alpha+1) \cdot \hspace{0.05cm} \text{... } \hspace{0.05cm} \cdot (2\alpha+n-2)} {(n-1)!}\cdot (1- {p_{\rm S} }^{1/\alpha})^{n-1} \hspace{0.05cm}.\]
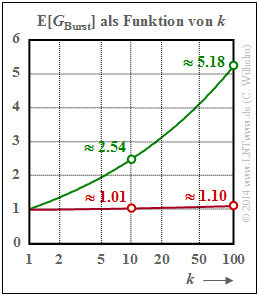
$\text{Beispiel 11:}\ \text{Mittlere Fehleranzahl } {\rm E}[G_{\rm Burst}] \text{ in einem Burst mit Endeparameter }k_{\rm Burst}$
Die mittlere Symbolfehlerwahrscheinlichkeit sei weiterhin $p_{\rm S} = 10^{-3}$, also (relativ) klein.
(1) Rote Kurve für den BSC–Kanal (bzw. $\alpha = 1)$:
- Der Parameter $k_{\rm Burst}= 10$ bedeutet beispielsweise, dass der Burst beendet ist, wenn nach einem Fehler neun fehlerfreie Symbole folgenden. Die Wahrscheinlichkeit für einen Fehlerabstand $a \le 9$ ist bei kleinem $p_{\rm S}$ $($hier: $10^{-3})$ äußerst klein. Daraus folgt weiter, dass dann (fast) jeder Einzelfehler als ein "Burst" aufgefasst wird, und es gilt ${\rm E}[G_{\rm Burst}] \approx 1.01$ .
- Bei größerem Burst–Endeparameter $k_{\rm Burst}$ nimmt auch die Wahrscheinlichkeit ${\rm Pr}(a \le k_{\rm Burst})$ deutlich zu und es kommt zu "Bursts" mit mehr als einem Fehler. Wählt man beispielsweise $k_{\rm Burst}= 100$, so beinhaltet ein "Burst" im Mittel $1.1$ Symbolfehler.
- Das bedeutet gleichzeitig, dass es auch beim BSC–Modell zu langen Fehlerbursts (entsprechend unserer Definition) kommen kann, wenn bei gegebenem $p_{\rm S}$ der Burst–Endeparameter zu groß gewählt ist oder bei vorgegebenem $k_{\rm Burst}$ die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ zu groß ist.
(2) Grüne Kurve für den Wilhelm–Kanal mit $\alpha = 0.7$:
Das hier angegebene Verfahren zur numerischen Bestimmung der mittleren Fehleranzahl ${\rm E}[G_{\rm Burst}]$ eines Bursts kann unabhängig vom $\alpha$–Wert angewendet werden. Man geht wie folgt vor:
- Entsprechend den Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a=k)$ generiert man eine Fehlerfolge $e_1$, $e_2$, ... , $e_i$, ... mit den Fehlerabständen $a_1$, $a_2$, ... , $a_i$, ...
- Ist ein Fehlerabstand $a_i \ge k_{\rm Burst}$, so markiert dieser das Ende eines Bursts. Ein solches Ereignis tritt mit der Wahrscheinlichkeit ${\rm Pr}(a \ge k_{\rm Burst}) = V_a(k_{\rm Burst} )$ ein.
- Wir zählen solche Ereignisse "$a_i \ge k_{\rm Burst}$" im gesamten Block der Länge $n$. Deren Anzahl ist gleichzeitig die Anzahl $N_{\rm Burst}$ der Bursts im Block.
- Gleichzeitig gilt die Beziehung $N_{\rm Burst} = N_{\rm Fehler} \cdot V_a(k_{\rm Burst} )$, wobei $N_{\rm Fehler}$ die Anzahl aller Fehler im Block angibt.
- Daraus lässt sich die mittlere Fehlerzahl pro Burst in einfacher Weise berechnen:
- \[{\rm E}[G_{\rm Burst}] =\frac {N_{\rm Fehler} }{N_{\rm Burst} } =\frac {1}{V_a(k_{\rm Burst})}\hspace{0.05cm}.\]
Die Markierungen in der Grafik korrespondieren mit folgenden Zahlenwerten der Fehlerabstandsverteilung:
- Die grünen Kreise $($Wilhelm–Kanal, $\alpha = 0.7)$ ergeben sich aus $V_a(10) = 0.394$ und $V_a(100) = 0.193$.
- Die roten Kreise $($BSC–Kanal, $\alpha = 1)$ sind die Kehrwerte von $V_a(10) = 0.991$ und $V_a(100) = 0906$.
Aufgaben zum Kapitel
Aufgabe 5.6: Fehlerkorrelationsdauer
Aufgabe 5.6Z: GE-Modelleigenschaften
Aufgabe 5.7: McCullough-Parameter aus Gilbert-Elliott-Parameter
Aufgabe 5.7Z: Nochmals McCullough-Modell
Quellenverzeichnis
- ↑ Gilbert, E. N.: Capacity of Burst–Noise Channel. In: Bell Syst. Techn. J. Vol. 39, 1960, pp. 1253–1266.
- ↑ Elliott, E.O.: Estimates of Error Rates for Codes on Burst–Noise Channels. In: Bell Syst. Techn. J., Vol. 42, (1963), pp. 1977 – 1997.
- ↑ Huber, J.: Codierung für gedächtnisbehaftete Kanäle. Dissertation – Universität der Bundeswehr München, 1982.
- ↑ McCullough, R.H.: The Binary Regenerative Channel. In: Bell Syst. Techn. J. (47), 1968.
- ↑ 5.0 5.1 5.2 Wilhelm, C.: A-Model and L-Model, New Channel Models with Formulas for Probabilities of Error Structures. Neue Kanalmodelle mit Formeln für die Wahrscheinlichkeit von Fehlerstrukturen. Internet-Veröffentlichungen zu Channels-Networks, 2011ff.