Difference between revisions of "Aufgaben:Exercise 5.1: Error Distance Distribution"
m (Text replacement - "Category:Aufgaben zu Digitalsignalübertragung" to "Category:Digital Signal Transmission: Exercises") |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Parameters_of_Digital_Channel_Models}} |
| − | [[File: | + | [[File:EN_Dig_A_5_1.png|right|frame|Error distance distribution]] |
| − | + | Any digital channel model can be described in the same way by | |
| − | * | + | * the error sequence $〈e_{\rm \nu}〉$, and |
| − | |||
| + | * the error distance sequence $〈a_{\rm \nu \hspace{0.05cm}'}〉$. | ||
| − | + | ||
| + | As an example, we consider the sequences: | ||
:$$<\hspace{-0.1cm}e_{\nu} \hspace{-0.1cm}> \ = \ < | :$$<\hspace{-0.1cm}e_{\nu} \hspace{-0.1cm}> \ = \ < | ||
\hspace{-0.1cm}0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, \text{...} | \hspace{-0.1cm}0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, \text{...} | ||
| Line 15: | Line 16: | ||
\hspace{-0.1cm}> \hspace{0.05cm}.$$ | \hspace{-0.1cm}> \hspace{0.05cm}.$$ | ||
| − | + | One can see from this, for example: | |
| − | * | + | * The error distance $a_2 = 3$ means that there are two error-free symbols between the first and the second error. |
| − | * | + | |
| + | * In contrast, $a_3 = 1$ indicates that the second error is immediately followed by a third. | ||
| − | + | The different indices $(\nu$ and $\nu\hspace{0.05cm} '$, each starting with $1$) are necessary because there is no synchrony between the error distance sequence and the error sequence. | |
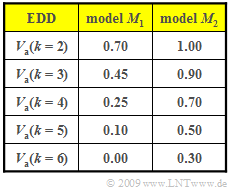
| − | In | + | In the graph, for two different models $M_1$ and $M_2$, the "error distance distribution" $\rm (EDD)$ is given as |
:$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}$$ | :$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}$$ | ||
| − | + | This table is to be evaluated in this exercise. | |
| − | |||
| − | |||
| − | + | Note: The exercise belongs to the chapter [[Digital_Signal_Transmission/Parameters_of_Digital_Channel_Models|"Parameters of Digital Channel Models"]]. | |
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the following error values $(0$ or $1)$? |
|type="{}"} | |type="{}"} | ||
$e_{\rm 16} \ = \ $ { 0. } | $e_{\rm 16} \ = \ $ { 0. } | ||
| Line 46: | Line 45: | ||
$e_{\rm 18} \ = \ $ { 1 } | $e_{\rm 18} \ = \ $ { 1 } | ||
| − | { | + | {What is the value of $V_a(k = 1)$ for both models? |
|type="{}"} | |type="{}"} | ||
$V_a(k = 1) \ = \ $ { 1 } | $V_a(k = 1) \ = \ $ { 1 } | ||
| − | { | + | {For model $M_1$, determine the probabilities of the error distances. |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(a = 1) \ = \ $ { 0.3 3% } | ${\rm Pr}(a = 1) \ = \ $ { 0.3 3% } | ||
| Line 58: | Line 57: | ||
${\rm Pr}(a = 5) \ = \ $ { 0.1 3% } | ${\rm Pr}(a = 5) \ = \ $ { 0.1 3% } | ||
| − | { | + | {What is the maximum possible error distance for model $M_1$? |
|type="{}"} | |type="{}"} | ||
$k_{\rm max} \ = \ ${ 5 } | $k_{\rm max} \ = \ ${ 5 } | ||
| − | { | + | {Calculate the average error distance for model $M_1$. |
|type="{}"} | |type="{}"} | ||
${\rm E}\big[a \big] \ = \ ${ 2.5 3% } | ${\rm E}\big[a \big] \ = \ ${ 2.5 3% } | ||
| − | { | + | {For model $M_1$, what is the mean error probability $p_{\rm M} = {\rm E}[e]$? |
|type="{}"} | |type="{}"} | ||
$p_{\rm M} \ = \ ${ 0.4 3% } | $p_{\rm M} \ = \ ${ 0.4 3% } | ||
| − | { | + | {Which statements are true for the model $M_2$ with certainty? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Two errors cannot directly follow each other. |
| − | - | + | - The most frequent error distance is $a = 6$. |
| − | - | + | - The mean error probability is $p_{\rm M} = 0.25$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Evaluation of the error distance sequence indicates errors at $\nu = 2, 5, 6, 10, 12, 17, 18, 19, 22, 26, 27$ and $29$. |
| − | * | + | |
| + | *It follows: $e_{\rm 16} \ \underline {= 0}$, $e_{\rm 17} \ \underline {= 1}$, $e_{\rm 18} \ \underline {= 1}$. | ||
| − | '''(2)''' | + | '''(2)''' From the definition equation follows already |
:$$V_a(k = 1) = {\rm Pr}(a \ge 1)\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$ | :$$V_a(k = 1) = {\rm Pr}(a \ge 1)\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' ${\rm Pr}(a = k) = V_a(k) \, –V_a(k+1)$ holds. From this we obtain for the individual probabilities: |
:$${\rm Pr}(a = 1)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(1) - V_a(2) = 1 - 0.7\hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$ | :$${\rm Pr}(a = 1)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(1) - V_a(2) = 1 - 0.7\hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$ | ||
:$${\rm Pr}(a = 2)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(2) - V_a(3) = 0.7 - 0.45 \hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm},$$ | :$${\rm Pr}(a = 2)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(2) - V_a(3) = 0.7 - 0.45 \hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm},$$ | ||
| Line 96: | Line 96: | ||
| − | '''(4)''' | + | '''(4)''' From $V_a(k=6) = {\rm Pr}(a ≥ 6) = 0$, it follows directly for the maximum error distance |
| + | :$$k_{\rm max} \ \underline {= 5}.$$ | ||
| − | '''(5)''' | + | '''(5)''' Using the probabilities calculated in subtask '''(3)''', the expected value we are looking for is: |
:$${\rm E}\big[a \big] = \sum_{k = 1}^{5} k \cdot {\rm Pr}(a = k) = 1 \cdot 0.3 +2 \cdot 0.25 +3 \cdot 0.2 +4 \cdot 0.15 +5 \cdot 0.1\hspace{0.15cm}\underline { = 2.5} | :$${\rm E}\big[a \big] = \sum_{k = 1}^{5} k \cdot {\rm Pr}(a = k) = 1 \cdot 0.3 +2 \cdot 0.25 +3 \cdot 0.2 +4 \cdot 0.15 +5 \cdot 0.1\hspace{0.15cm}\underline { = 2.5} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | '''(6)''' The mean error probability is the inverse of the average error distance: |
| + | :$$p_{\rm M} \ \underline {= 0.4}.$$ | ||
| + | |||
| + | |||
| + | '''(7)''' With certainty, only <u>statement 1</u> is true: | ||
| + | *The first statement is true because ${\rm Pr}(a = 1) = V_a(1) - V_a(2) = 0$. | ||
| + | |||
| + | * The second statement is not certain because $V_a(6)$ gives only the sum of the probabilities ${\rm Pr}(a ≥ 6)$, but not ${\rm Pr}(a = 6)$ alone. | ||
| + | *Only with the additional specification $V_a(7) = 0$ would statement 2 be true. | ||
| − | + | * Likewise, for the expected value ${\rm E}[a]$, no definite statement is possible due to missing information. With $V_a(7) = 0$ the result would be: | |
| − | * | ||
| − | |||
| − | |||
| − | |||
:$${\rm E}[a] = 2 \cdot 0.1 +3 \cdot 0.2 +4 \cdot 0.2 +5 \cdot 0.2 +6 \cdot 0.3= | :$${\rm E}[a] = 2 \cdot 0.1 +3 \cdot 0.2 +4 \cdot 0.2 +5 \cdot 0.2 +6 \cdot 0.3= | ||
| − | 4.4$$ | + | 4.4.$$ |
| − | * | + | *Without this specification, only the statement ${\rm E}[a] ≥ 4.4$ is possible. But this means that the condition $p_{\rm M} < 1/4.4 < 0.227$ is valid for the mean error probability. Statement 3 is therefore also not true with certainty. |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Digital Signal Transmission: Exercises|^5.1 | + | [[Category:Digital Signal Transmission: Exercises|^5.1 Digital Channel Models^]] |
Latest revision as of 14:13, 1 October 2022
Any digital channel model can be described in the same way by
- the error sequence $〈e_{\rm \nu}〉$, and
- the error distance sequence $〈a_{\rm \nu \hspace{0.05cm}'}〉$.
As an example, we consider the sequences:
- $$<\hspace{-0.1cm}e_{\nu} \hspace{-0.1cm}> \ = \ < \hspace{-0.1cm}0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, \text{...} \hspace{-0.1cm}> \hspace{0.05cm},$$
- $$< \hspace{-0.1cm}a_{\nu\hspace{0.05cm} '} \hspace{-0.15cm}> \ = \ <\hspace{-0.1cm}2, 3, 1, 4, 2, 5, 1, 1, 3, 4, 1, 2, \text{...} \hspace{-0.1cm}> \hspace{0.05cm}.$$
One can see from this, for example:
- The error distance $a_2 = 3$ means that there are two error-free symbols between the first and the second error.
- In contrast, $a_3 = 1$ indicates that the second error is immediately followed by a third.
The different indices $(\nu$ and $\nu\hspace{0.05cm} '$, each starting with $1$) are necessary because there is no synchrony between the error distance sequence and the error sequence.
In the graph, for two different models $M_1$ and $M_2$, the "error distance distribution" $\rm (EDD)$ is given as
- $$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}$$
This table is to be evaluated in this exercise.
Note: The exercise belongs to the chapter "Parameters of Digital Channel Models".
Questions
Solution
- It follows: $e_{\rm 16} \ \underline {= 0}$, $e_{\rm 17} \ \underline {= 1}$, $e_{\rm 18} \ \underline {= 1}$.
(2) From the definition equation follows already
- $$V_a(k = 1) = {\rm Pr}(a \ge 1)\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$
(3) ${\rm Pr}(a = k) = V_a(k) \, –V_a(k+1)$ holds. From this we obtain for the individual probabilities:
- $${\rm Pr}(a = 1)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(1) - V_a(2) = 1 - 0.7\hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$
- $${\rm Pr}(a = 2)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(2) - V_a(3) = 0.7 - 0.45 \hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm},$$
- $${\rm Pr}(a = 3)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(3) - V_a(4) = 0.45 - 0.25 \hspace{0.15cm}\underline {= 0.2}\hspace{0.05cm},$$
- $${\rm Pr}(a = 4)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(4) - V_a(5) = 0.25 - 0.10 \hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$
- $${\rm Pr}(a = 5)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(5) - V_a(6) = 0.10 - 0 \hspace{0.15cm}\underline {= 0.10}\hspace{0.05cm}.$$
(4) From $V_a(k=6) = {\rm Pr}(a ≥ 6) = 0$, it follows directly for the maximum error distance
- $$k_{\rm max} \ \underline {= 5}.$$
(5) Using the probabilities calculated in subtask (3), the expected value we are looking for is:
- $${\rm E}\big[a \big] = \sum_{k = 1}^{5} k \cdot {\rm Pr}(a = k) = 1 \cdot 0.3 +2 \cdot 0.25 +3 \cdot 0.2 +4 \cdot 0.15 +5 \cdot 0.1\hspace{0.15cm}\underline { = 2.5} \hspace{0.05cm}.$$
(6) The mean error probability is the inverse of the average error distance:
- $$p_{\rm M} \ \underline {= 0.4}.$$
(7) With certainty, only statement 1 is true:
- The first statement is true because ${\rm Pr}(a = 1) = V_a(1) - V_a(2) = 0$.
- The second statement is not certain because $V_a(6)$ gives only the sum of the probabilities ${\rm Pr}(a ≥ 6)$, but not ${\rm Pr}(a = 6)$ alone.
- Only with the additional specification $V_a(7) = 0$ would statement 2 be true.
- Likewise, for the expected value ${\rm E}[a]$, no definite statement is possible due to missing information. With $V_a(7) = 0$ the result would be:
- $${\rm E}[a] = 2 \cdot 0.1 +3 \cdot 0.2 +4 \cdot 0.2 +5 \cdot 0.2 +6 \cdot 0.3= 4.4.$$
- Without this specification, only the statement ${\rm E}[a] ≥ 4.4$ is possible. But this means that the condition $p_{\rm M} < 1/4.4 < 0.227$ is valid for the mean error probability. Statement 3 is therefore also not true with certainty.