Difference between revisions of "Digital Signal Transmission/Burst Error Channels"
| (74 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Digital Channel Models |
|Vorherige Seite=Binary Symmetric Channel (BSC) | |Vorherige Seite=Binary Symmetric Channel (BSC) | ||
|Nächste Seite=Anwendungen bei Multimedia–Dateien | |Nächste Seite=Anwendungen bei Multimedia–Dateien | ||
}} | }} | ||
| − | == | + | == Channel model according to Gilbert-Elliott== |
<br> | <br> | ||
| − | + | This channel model, which goes back to [https://en.wikipedia.org/wiki/Edgar_Gilbert E. N. Gilbert] [Gil60]<ref name='Gil60'>Gilbert, E. N.: Capacity of Burst–Noise Channel. In: Bell Syst. Techn. J. Vol. 39, 1960, pp. 1253–1266.</ref> and E. O. Elliott [Ell63]<ref name='Ell63'>Elliott, E.O.: Estimates of Error Rates for Codes on Burst–Noise Channels. In: Bell Syst. Techn. J., Vol. 42, (1963), pp. 1977 – 1997.</ref>, is suitable for describing and simulating "digital transmission systems with burst error characteristics". | |
| − | [[File:P ID1835 Dig T 5 3 S1 version1.png| | + | The '''Gilbert–Elliott model''' $($abbreviation: "GE model"$)$ can be characterized as follows: |
| + | [[File:P ID1835 Dig T 5 3 S1 version1.png|right|frame|Gilbert-Elliott channel model with two states<br><br><br>|class=fit]] | ||
| − | + | *The different transmission quality at different times is expressed by a finite number $g$ of channel states $(Z_1, Z_2,\hspace{0.05cm} \text{...} \hspace{0.05cm}, Z_g)$. <br> | |
| − | |||
| − | * | + | *The in reality smooth transitions of the interference intensity – in the extreme case from completely error-free transmission to total failure – are approximated in the GE model by fixed probabilities in the individual channel states.<br> |
| − | * | + | *The transitions between the $g$ states occur according to a [[Theory_of_Stochastic_Signals/Markov_Chains|"Markov process"]] (1st order) and are characterized by $g \cdot (g-1)$ transition probabilities. Together with the $g$ error probabilities in the individual states, there are thus $g^2$ free model parameters.<br> |
| − | * | + | *For reasons of mathematical manageability, one usually restricts oneself to $g = 2$ states and denotes these with $\rm G$ ("GOOD") and $\rm B$ ("BAD"). Mostly, the error probability in state $\rm G$ will be much smaller than in state $\rm B$.<br> |
| − | * | + | *In that what follows, we use these two error probabilities $p_{\rm G}$ and $p_{\rm B}$, where $p_{\rm G} < p_{\rm B}$ should hold, as well as the transition probabilities ${\rm Pr}({\rm B}\hspace{0.05cm}|\hspace{0.05cm}{\rm G})$ and ${\rm Pr}({\rm G}\hspace{0.05cm}|\hspace{0.05cm}{\rm B})$. This also determines the other two transition probabilities: |
::<math>{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) = 1 - {\rm | ::<math>{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) = 1 - {\rm | ||
| Line 28: | Line 28: | ||
G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{0.05cm}.</math> | G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{0.05cm}.</math> | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We consider the Gilbert-Elliott model with the parameters |
| + | [[File:P ID1837 Dig T 5 3 S1b version1.png|right|frame|Example Gilbert-Elliott error sequence|class=fit]] | ||
| + | |||
| + | :$$p_{\rm G} = 0.01,$$ | ||
| + | :$$p_{\rm B} = 0.4,$$ | ||
| + | :$${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) = | ||
| + | 0.1, $$ | ||
| + | :$$ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} | ||
| + | G) = 0.01\hspace{0.05cm}.$$ | ||
| + | The underlying model is shown at the end of this example with the parameters given here. | ||
| + | |||
| + | The upper graphic shows a (possible) error sequence of length $N = 800$. If the GE model is in the "BAD" state, this is indicated by the gray background. | ||
| + | |||
| + | To simulate such a GE error sequence, switching is performed between the states "GOOD" and "BAD" according to the four transition probabilities. | ||
| + | |||
| + | *At the first clock call, the selection of the state is expediently done according to the "state probabilities" $w_{\rm G}$ and $w_{\rm B}$, as calculated below.<br> | ||
| − | + | *At each clock cycle, exactly one element of the error sequence $ \langle e_\nu \rangle$ is generated according to the current error probability $(p_{\rm G}$ or $p_{\rm B})$. | |
| − | |||
| − | |||
| − | |||
| − | + | *The [[Digital_Signal_Transmission/Burst_Error_Channels#Channel_model_according_to_McCullough|"error distance simulation"]] is not applicable here, because in the GE model a state change is possible after each symbol $($and not only after an error$)$. | |
| − | |||
| − | + | The probabilities that the Markov chain is in the "GOOD" or "BAD" state can be calculated from the assumed homogeneity and stationarity. | |
| − | + | One obtains with the above numerical values: | |
::<math>w_{\rm G} = | ::<math>w_{\rm G} = | ||
| − | {\rm Pr( | + | {\rm Pr(in\hspace{0.15cm} state \hspace{0.15cm}G)}= |
\frac{ {\rm Pr}(\rm | \frac{ {\rm Pr}(\rm | ||
G\hspace{0.05cm}\vert\hspace{0.05cm} B)}{ {\rm Pr}(\rm | G\hspace{0.05cm}\vert\hspace{0.05cm} B)}{ {\rm Pr}(\rm | ||
| Line 53: | Line 63: | ||
{10}/{11}\hspace{0.05cm},</math> | {10}/{11}\hspace{0.05cm},</math> | ||
::<math>w_{\rm B} = | ::<math>w_{\rm B} = | ||
| − | {\rm Pr( | + | {\rm Pr(in\hspace{0.15cm} state \hspace{0.15cm}B)}= |
\frac{ {\rm Pr}(\rm | \frac{ {\rm Pr}(\rm | ||
B\hspace{0.05cm}\vert\hspace{0.05cm} G)}{ {\rm Pr}(\rm | B\hspace{0.05cm}\vert\hspace{0.05cm} G)}{ {\rm Pr}(\rm | ||
| Line 59: | Line 69: | ||
B\hspace{0.05cm}\vert\hspace{0.05cm} G)} = \frac{0.11}{0.1 + 0.01} = | B\hspace{0.05cm}\vert\hspace{0.05cm} G)} = \frac{0.11}{0.1 + 0.01} = | ||
{1}/{11}\hspace{0.05cm}.</math> | {1}/{11}\hspace{0.05cm}.</math> | ||
| + | [[File:P ID1836 Dig T 5 3 S1a version1.png|right|frame|Considered Gilbert-Elliott model|class=fit]] | ||
| − | + | These two state probabilities can also be used to determine the "mean error probability" of the GE model: | |
::<math>p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} | ::<math>p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} | ||
| Line 69: | Line 80: | ||
B\hspace{0.05cm}\vert\hspace{0.05cm} G)} \hspace{0.05cm}.</math> | B\hspace{0.05cm}\vert\hspace{0.05cm} G)} \hspace{0.05cm}.</math> | ||
| − | + | In particular, for the model considered here as an example: | |
::<math>p_{\rm M} ={10}/{11} \cdot 0.01 +{1}/{11} \cdot 0.4 = | ::<math>p_{\rm M} ={10}/{11} \cdot 0.01 +{1}/{11} \cdot 0.4 = | ||
| − | {1}/{22} \approx 4.55\%\hspace{0.05cm}.</math> | + | {1}/{22} \approx 4.55\%\hspace{0.05cm}.</math>}}<br> |
| − | + | == Error distance distribution of the Gilbert-Elliott model == | |
| + | <br> | ||
| + | [[File:EN_Dig_T_5_3_S2.png|right|frame|Error distance distribution of GE and BSC model|class=fit]] | ||
| + | In [Hub82]<ref name = 'Hub82'>Huber, J.: Codierung für gedächtnisbehaftete Kanäle. Dissertation – Universität der Bundeswehr München, 1982.</ref> you can find the analytical computations | ||
| − | + | *of the "probability of the error distance $k$": | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
::<math>{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm | ::<math>{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm | ||
| Line 88: | Line 97: | ||
B})\hspace{0.05cm},</math> | B})\hspace{0.05cm},</math> | ||
| − | * | + | *the [[Digital_Signal_Transmission/Parameters_of_Digital_Channel_Models#Error_distance_distribution|"error distance distribution"]] $\rm (EDD)$: |
::<math>V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm | ::<math>V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm | ||
| Line 95: | Line 104: | ||
B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.</math> | B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.</math> | ||
| − | + | The following auxiliary quantities are used here: | |
::<math>u_{\rm GG} ={\rm Pr}(\rm | ::<math>u_{\rm GG} ={\rm Pr}(\rm | ||
| Line 126: | Line 135: | ||
\hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.</math> | \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.</math> | ||
| − | + | The given equations are the result of extensive matrix operations.<br> | |
| + | |||
| + | The upper graph shows the error distance distribution $\rm (EDD)$ of the Gilbert-Elliott model (red curve) in linear and logarithmic representation for the parameters | ||
| + | :$${\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B ) = 0.1 \hspace{0.05cm},\hspace{0.5cm}{\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G ) = 0.01 \hspace{0.05cm},\hspace{0.5cm}p_{\rm G} = 0.001, \hspace{0.5cm}p_{\rm B} = 0.4.$$ | ||
| − | + | For comparison, the corresponding $V_a(k)$ curve for the BSC model with the same mean error probability $p_{\rm M} = 4.5\%$ is also plotted as blue curve.<br> | |
| − | + | == Error correlation function of the Gilbert-Elliott model == | |
| − | + | <br> | |
| − | + | For the [[Digital_Signal_Transmission/Parameters_of_Digital_Channel_Models#Error_correlation_function|"error correlation function"]] $\rm (ECF)$ of the GE model with | |
| + | *the mean error probability $p_{\rm M}$, | ||
| + | |||
| + | *the transition probabilities ${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )$ and ${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )$ as well as | ||
| − | + | *the error probabilities $p_{\rm G}$ and $p_{\rm B}$ in the two states $\rm G$ and $\rm B$, | |
| − | |||
| − | |||
| − | |||
| − | ::<math>\varphi_{e}(k) = {\rm E}[e_\nu \cdot e_{\nu +k}] = | + | we obtain after extensive matrix operations the relatively simple expression |
| + | |||
| + | ::<math>\varphi_{e}(k) = {\rm E}\big[e_\nu \cdot e_{\nu +k}\big] = | ||
\left\{ \begin{array}{c} p_{\rm M} \\ | \left\{ \begin{array}{c} p_{\rm M} \\ | ||
p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) (p_{\rm M} - p_{\rm G}) | p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) (p_{\rm M} - p_{\rm G}) | ||
| Line 146: | Line 162: | ||
B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm | B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} B )]^k \end{array} \right.\quad | G\hspace{0.05cm}|\hspace{0.05cm} B )]^k \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} f{\rm | + | \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, |
| − | \\ f{\rm | + | \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}</math> |
| + | |||
| + | For the Gilbert-Elliott model, for "renewing models" $\varphi_{e}(k)$ must always be calculated according to this equation. The iterative calculation algorithm for "renewing models", | ||
| + | :$$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot | ||
| + | \varphi_{e}(k - \kappa), $$ | ||
| + | |||
| + | cannot be applied here, since the GE model is not renewing ⇒ here, the error distances are not statistically independent of each other. | ||
| − | + | [[File:P ID1839 Dig T 5 3 S3 version1.png|right|frame|Error correlation function of "GE" (circles) and "BSC" (crosses)|class=fit]] | |
| − | + | The graph shows an example of the ECF curve of the Gilbert-Elliott model marked with red circles. One can see from this representation: | |
| + | *While for the memoryless channel $($BSC model, blue curve$)$ all ECF values are $\varphi_{e}(k \ne 0)= p_{\rm M}^2$, the ECF values approach this final value for the burst error channel much more slowly.<br> | ||
| − | + | *At the transition from $k = 0$ to $k = 1$ a certain discontinuity occurs. While $\varphi_{e}(k = 0)= p_{\rm M}$, the second equation valid for $k > 0$ yields the following extrapolated value for $k = 0$: | |
| − | |||
| − | |||
| − | |||
::<math>\varphi_{e0} = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm | ::<math>\varphi_{e0} = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm | ||
M} - p_{\rm G})\hspace{0.05cm}.</math> | M} - p_{\rm G})\hspace{0.05cm}.</math> | ||
| − | * | + | *A quantitative measure of the length of the statistical ties is the "correlation duration" $D_{\rm K}$, which is defined as the width of an equal-area rectangle of height $\varphi_{e0} - p_{\rm M}^2$: |
::<math>D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 | ::<math>D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 | ||
| − | }^{\infty}\hspace{0.1cm} [\varphi_{e}(k) - p_{\rm | + | }^{\infty}\hspace{0.1cm} \big[\varphi_{e}(k) - p_{\rm |
| − | M}^2]\hspace{0.05cm}.</math> | + | M}^2\big ]\hspace{0.05cm}.</math> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusions:}$ In the Gilbert–Elliott model, the "correlation duration" is given by the simple, analytically expressible expression |
::<math>D_{\rm K} =\frac{1}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} | ::<math>D_{\rm K} =\frac{1}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} | ||
| Line 173: | Line 193: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *$D_{\rm K}$ | + | *$D_{\rm K}$ is larger the smaller ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} |
| − | G )$ | + | G )$ and ${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ are, i.e., when state changes occur rarely. |
| − | |||
| − | == | + | *For the BSC model ⇒ $p_{\rm B}= p_{\rm G} = p_{\rm M}$ ⇒ $D_{\rm K} = 0$, this equation is not applicable.}}<br> |
| + | |||
| + | == Channel model according to McCullough== | ||
<br> | <br> | ||
| − | + | The main disadvantage of the Gilbert–Elliott model is that it does not allow error distance simulation. As will be worked out in [[Aufgaben:Exercise_5.5:_Error_Sequence_and_Error_Distance_Sequence|"Exercise 5.5"]], this has great advantages over the symbol-wise generation of the error sequence $\langle e_\nu \rangle$ in terms of computational speed and memory requirements.<br> | |
| − | McCullough [McC68]<ref name ='McC68'>McCullough, R.H.: | + | *McCullough [McC68]<ref name ='McC68'>McCullough, R.H.: The Binary Regenerative Channel. In: Bell Syst. Techn. J. (47), 1968.</ref> modified the model developed three years earlier by Gilbert and Elliott so |
| + | *that an error distance simulation in the two states "GOOD" and "BAD" is applicable in each case by itself. | ||
| + | [[File:EN_Dig_T_5_3_S4a.png|right|frame|Channel models according to Gilbert-Elliott and McCullough |class=fit]] | ||
| − | |||
| − | + | The graph shows McCullough's model, hereafter referred to as the "MC model", while the "GE model" is shown above after renaming the transition probabilities ⇒ ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, etc.<br> | |
| − | |||
| − | + | There are many similarities and a few differences between the two models: | |
| − | + | #Like the Gilbert–Elliott model, the McCullough channel model is based on a "first-order Markov process" with the two states "GOOD" $(\rm G)$ and "BAD" $(\rm B)$. No difference can be found with respect to the model structure.<br> | |
| − | + | #The main difference to the Gilbert–Elliott is that a change of state between "GOOD" and "BAD" is only possible after an error – i.e. a "$1$" in the error sequence. This enables an "error distance simulation".<br> | |
| − | + | #The four freely selectable GE parameters $p_{\rm G}$, $p_{\rm B}$, ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$, ${\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ can be converted into the MC parameters $q_{\rm G}$, $q_{\rm B}$, ${\it q}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$, ${\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ in such a way that an error sequence with the same statistical properties as in the GE model is generated. See next section.<br> | |
| − | + | #For example, ${\it q}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ denotes the transition probability from "GOOD" to "BAD" under the condition '''that an error has just occurred'''. The comparable GE parameter ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ characterizes this transition probability without this additional condition.<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The figure above shows an exemplary error sequence of the Gilbert-Elliott model with the parameters |
| + | [[File:EN_Dig_T_5_3_S4.png|right|frame|Error sequence of the GE model (top) and the equivalent MC model (bottom)|class=fit]] | ||
| − | + | :$$p_{\rm G} = 0.01,$$ | |
| + | :$$p_{\rm B} = 0.4,$$ | ||
| + | :$${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) = | ||
| + | 0.1, $$ | ||
| + | :$$ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} | ||
| + | G) = 0.01\hspace{0.05cm}.$$ | ||
| + | An error sequence of the equivalent McCullough model is drawn below. The relations between the two models can be summarized as follows: | ||
| + | #In the GE error sequence, a change from state "GOOD" (white background) to state "BAD" (gray background) and vice versa is possible at any time $\nu$, even when $e_\nu = 0$. | ||
| + | #In contrast, in the ML error sequence, a change of state at time $\nu$ is only possible at $e_\nu = 1$. The last error value before a gray background is always "$1$".<br> | ||
| + | #With the ML model one does not have to generate the errors "step–by–step", but can use the faster error distance simulation ⇒ see [[Aufgaben:Exercise_5.5:_Error_Sequence_and_Error_Distance_Sequence|"Exercise 5.5"]].<br> | ||
| + | #The GE parameters can be converted into corresponding MC parameters in such a way that the two models are equivalent ⇒ see next section. | ||
| + | #That means: The MC error sequence has exactly same statistical properties as the GE sequence. But, it does '''not''' mean that both error sequences are identical.}}<br><br> | ||
| − | + | == Conversion of the GE parameters into the MC parameters == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| − | + | The parameters of the equivalent MC model can be calculated from the GE parameters as follows: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | :: | + | :$$q_{\rm G} =1-\beta_{\rm |
| + | G}\hspace{0.05cm},$$ | ||
| + | :$$ q_{\rm | ||
| + | B} = 1-\beta_{\rm B}\hspace{0.05cm}, $$ | ||
| + | :$$q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) =\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm | ||
B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm | B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm | G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm | ||
| − | B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm}, | + | B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm},$$ |
| − | q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = | + | :$$q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = |
\frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm | \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm | ||
| − | B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}. | + | B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$ |
| − | + | *Here again the following auxiliary quantities are used: | |
::<math>u_{\rm GG} = {\rm Pr}(\rm | ::<math>u_{\rm GG} = {\rm Pr}(\rm | ||
| Line 240: | Line 263: | ||
{\it u}_{\rm BG} ={\rm Pr}(\rm | {\it u}_{\rm BG} ={\rm Pr}(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm | G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm | ||
| − | B}) | + | B})</math> |
| − | |||
::<math>\Rightarrow \hspace{0.3cm} \beta_{\rm G} = \frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - | ::<math>\Rightarrow \hspace{0.3cm} \beta_{\rm G} = \frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - | ||
u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} | u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} | ||
| − | \hspace{0.05cm}, | + | \hspace{0.05cm}, |
| − | + | \hspace{0.9cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm | |
GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot | GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot | ||
u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.</math> | u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.</math> | ||
| − | :<math>x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} | + | ::<math>x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} |
\hspace{0.05cm},\hspace{0.2cm} | \hspace{0.05cm},\hspace{0.2cm} | ||
| − | x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}} | + | x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}} |
| − | + | \Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot | |
| − | |||
p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm | p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm | ||
B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, | B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, | ||
| − | \hspace{0. | + | \hspace{0.9cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.</math> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ As in [[Digital_Signal_Transmission/Burst_Error_Channels#Channel_model_according_to_McCullough|$\text{Example 2}$]], the GE parameters are: |
| − | :$$p_{\rm G} = 0.01, \ p_{\rm B} = 0.4, \ p(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01, \ {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1.$$ | + | :$$p_{\rm G} = 0.01, \hspace{0.5cm} p_{\rm B} = 0.4, \hspace{0.5cm} p(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01, \hspace{0.5cm} {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1.$$ |
| − | + | Applying the above equations, we then obtain for the equivalent MC parameters: | |
| − | :$$q_{\rm G} = 0.0186, \ q_{\rm B} = 0.4613, \ q(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.3602, \ {\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.2240.$$ | + | :$$q_{\rm G} = 0.0186, \hspace{0.5cm} q_{\rm B} = 0.4613, \hspace{0.5cm} q(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.3602, \hspace{0.5cm} {\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.2240.$$ |
| − | * | + | *If we compare in $\text{Example 2}$ the red error sequence $($GE, change of state is always possible$)$ with the blue sequence $($equivalent MC, change of state only at $e_\nu = 1$$)$, we can see quite serious differences. |
| − | |||
| − | + | * But the blue error sequence of the equivalent McCullough model has exactly the same statistical properties as the red error sequence of the Gilbert-Elliott model.}} | |
| − | == | + | |
| + | The conversion of the GE parameters to the MC parameters is illustrated in [[Aufgaben:Aufgabe_5.7:_McCullough-Parameter_aus_Gilbert-Elliott-Parameter|"Exercise 5.7"]] using a simple example. [[Aufgaben:Aufgabe_5.7Z:_Nochmals_McCullough-Modell|"Exercise 5.7Z"]] further shows how they can be determined directly from the $q$ parameters: | ||
| + | #the mean error probability, | ||
| + | #the error distance distribution, | ||
| + | #the error correlation function and | ||
| + | #the correlation duration of the MC model. <br> | ||
| + | |||
| + | == Burst error channel model according to Wilhelm == | ||
<br> | <br> | ||
| − | + | This model goes back to [[Biographies_and_Bibliographies/External_Contributors_to_LNTwww#Dr._sc._techn._Claus_Wilhelm|Claus Wilhelm]] and was developed from the mid-1960s onwards from empirical measurements of temporal consequences of bit errors. | |
| + | *It is based on thousands of measurement hours in transmission channels from $\text{200 bit/s}$ with analog modem up to $\text{2.048 Mbit/s}$ via [[Examples_of_Communication_Systems/General_Description_of_ISDN|"ISDN"]]. | ||
| + | [[File:EN_Dig_T_5_3_S5.png|right|frame|Exemplary function curves $h_{\rm B}(n)$. $\rm KW$: "short wave", $\rm UKW$: "ultra short wave"]] | ||
| + | *Likewise, marine radio channels up to $7500$ kilometers in the shortwave range were measured.<br> | ||
| − | |||
| − | |||
| − | + | Blocks of length $n$ were recorded. The respective block error rate $h_{\rm B}(n)$ was determined from this. <u>Note.</u> | |
| + | # A block error is already present if even one of the $n$ symbols has been falsified. | ||
| + | #Knowing well that the "block error rate" $h_{\rm B}(n)$ corresponds exactly to the "block error probability" $p_{\rm B}$ only for $n \to \infty$, we set $p_{\rm B}(n) \approx h_{\rm B}(n)$ in the following description.<br> | ||
| + | #In another context, $p_{\rm B}$ sometimes also denotes the "bit error probability" in our learning tutorial. | ||
| − | ::<math>{\rm lg} \hspace{0. | + | |
| + | In a large number of measurements, the fact that | ||
| + | |||
| + | ⇒ the course $p_{\rm B}(n)$ in double-logarithmic representation shows linear increases in the lower range | ||
| + | |||
| + | has been confirmed again and again $($see graph$)$. Thus, it holds for $n \le n^\star$: | ||
| + | |||
| + | ::<math>{\rm lg} \hspace{0.15cm}p_{\rm B}(n) = {\rm lg} \hspace{0.15cm}p_{\rm S} + \alpha \cdot {\rm lg} \hspace{0.15cm}n\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\hspace{0.05cm}.</math> | \Rightarrow \hspace{0.3cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\hspace{0.05cm}.</math> | ||
| − | + | #Here, $p_{\rm S} = p_{\rm B}(n=1)$ denotes the mean symbol error probability. | |
| + | #The empirically found values of $\alpha$ are between $0.5$ and $0.95$. | ||
| + | #For $1-\alpha$, the term "burst factor" is also used. | ||
<br clear = all> | <br clear = all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ In the BSC model, the course of the block error probability is: |
::<math>p_{\rm B}(n) =1 -(1 -p_{\rm S})^n \approx n \cdot p_{\rm S}\hspace{0.05cm}.</math> | ::<math>p_{\rm B}(n) =1 -(1 -p_{\rm S})^n \approx n \cdot p_{\rm S}\hspace{0.05cm}.</math> | ||
| − | + | From this follows $\alpha = 1$ and the burst factor $1-\alpha = 0$. In this case $($and only in this case$)$ a linear course results even with non-logarithmic representation.<br> | |
| − | + | *Note that the above approximation is only valid for $p_{\rm S} \ll 1$ and not too large $n$, otherwise the approximation $(1-p_{\rm S})^n \approx1 - n \cdot p_{\rm S}$ is not applicable. | |
| + | |||
| + | *But this also means that the equation given above is also only valid for a lower range $($for $n < n^\star)$. | ||
| + | |||
| + | *Otherwise, an infinitely large block error probability would result for $n \to \infty$. }}<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ For the function $p_{\rm B}(n)$ ⇒ "block error probability" determined empirically from measurements, we now have to find the [[Digital_Signal_Transmission/Parameters_of_Digital_Channel_Models#Error_distance_distribution|'''error distance distribution''']] $\rm (EDD)$ from which the course for $n > n^\star$ can be extrapolated, which satisfies the following constraint: |
| − | ::<math>\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_{\rm B}(n) = 1 </math> | + | ::<math>\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_{\rm B}(n) = 1 .</math> |
| − | + | *We refer to this approach as the '''Wilhelm model'''. | |
| − | == | + | *Since memory extends only to the last symbol error, this model is a renewal model.}}<br> |
| + | |||
| + | == Error distance consideration to the Wilhelm model == | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We now consider the error distances. An "error sequence" $\langle e_\nu \rangle$ can be equivalently represented by the "error distance sequence" $\langle a_{\nu\hspace{0.06cm}'} \rangle$, as shown in the following graph. It can be seen: | |
| − | * | + | #The error sequence "$\text{...}\rm 1001\text{...}$" is expressed by "$a= 3$". <br> |
| + | #Accordingly, the error distance "$a= 1$" denotes the error sequence "$\text{...}\rm 11\text{...}$".<br> | ||
| + | #The different indices $\nu$ and $\nu\hspace{0.06cm}'$ take into account that the two sequences do not run synchronously. | ||
| + | |||
| + | |||
| + | With the probabilities $p_a(k) = {\rm Pr}(a= k)$ for the individual error distances $k$ and the mean symbol error probability $p_{\rm S}$, the following definitions apply for | ||
| + | [[File:P ID2807 Dig T 5 3 S5b.png|right|frame|Error sequence $\langle e_\nu \rangle$ and error distance sequence $\langle a_{\nu\hspace{0.06cm}'} \rangle$|class=fit]] | ||
| + | * the "error distance distribution" $\rm (EDD)$: | ||
::<math> V_a(k) = {\rm Pr}(a \ge k)= \sum_{\kappa = k}^{\infty}p_a(\kappa) \hspace{0.05cm},</math> | ::<math> V_a(k) = {\rm Pr}(a \ge k)= \sum_{\kappa = k}^{\infty}p_a(\kappa) \hspace{0.05cm},</math> | ||
| − | * | + | * the "mean error distance" ${\rm E}\big[a\big]$: |
| − | ::<math> V_a(k) = {\rm E}[a] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = {1}/{p_{\rm S}}\hspace{0.05cm}.</math> | + | ::<math> V_a(k) = {\rm E}\big[a\big] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = {1}/{p_{\rm S}}\hspace{0.05cm}.</math> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
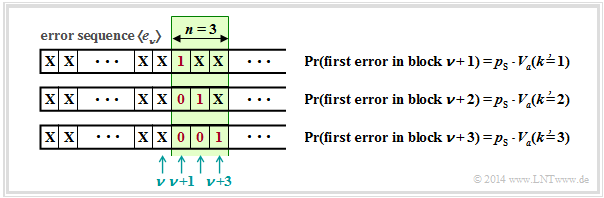
| − | $\text{ | + | $\text{Example 5:}$ We consider a block with $n$ bits, starting at bit position $\nu + 1$. |
| − | |||
| − | |||
| − | + | [[File:EN_Dig_T_5_3_S5c.png|right|frame|To derive the Wilhelm model|class=fit]] | |
| − | + | <u>Some comments:</u> | |
| + | #A block error occurs whenever a bit is falsified at positions $\nu + 1$, ... , $\nu + n$. <br> | ||
| + | #The falsification probabilities are expressed in the graph by the error distance distribution ${V_a}\hspace{0.06cm}'(k)$. | ||
| + | #Somewhere before the block of length $n = 3$ is the last error, but at least at distance $k$ from the first error in the block. | ||
| + | #So the distance is equal or greater than $k$, which corresponds exactly to the probability ${V_a}'(k)$. | ||
| + | #The apostrophe is to indicate that a correction has to be made later to get from the empirically found error distance distribution to the correct function ${V_a}(k)$. }} | ||
| − | |||
| − | + | We now have several equations for the block error probability $p_{\rm B}(n)$. | |
| − | + | *A first equation establishes the relationship between $p_{\rm B}(n)$ and the (approximate) error distance distribution ${V_a}'(k)$: | |
| − | * | + | ::<math>(1)\hspace{0.4cm} p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) \hspace{0.05cm}, |
| − | ::<math>(1)\hspace{0. | ||
</math> | </math> | ||
| − | * | + | *A second equation is provided by our empirical investigation at the beginning of this section: |
| − | ::<math>(2)\hspace{0. | + | ::<math>(2)\hspace{0.4cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}</math> |
| − | * | + | *The third equation is obtained by equating $(1)$ and $(2)$: |
| − | ::<math>(3)\hspace{0. | + | ::<math>(3)\hspace{0.4cm} |
\sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) = n^{\alpha} \hspace{0.05cm}. </math> | \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) = n^{\alpha} \hspace{0.05cm}. </math> | ||
| − | + | By successively substituting $n = 1, 2, 3,$ ... into this equation, we obtain with ${V_a}'(k = 1) = 1$: | |
::<math>V_a\hspace{0.05cm}'(1) = 1^{\alpha} | ::<math>V_a\hspace{0.05cm}'(1) = 1^{\alpha} | ||
| Line 344: | Line 393: | ||
\hspace{0.35cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}'(k) = k^{\alpha}-(k-1)^{\alpha} \hspace{0.05cm}.</math> | \hspace{0.35cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}'(k) = k^{\alpha}-(k-1)^{\alpha} \hspace{0.05cm}.</math> | ||
| − | + | However, the coefficients ${V_a}'(k)$ obtained from empirical data do not necessarily satisfy the normalization condition. | |
| + | |||
| + | To correct the issue, Wilhelm uses the following approach: | ||
::<math>V_a\hspace{0.05cm}(k) = V_a\hspace{0.05cm}'(k) \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ::<math>V_a\hspace{0.05cm}(k) = V_a\hspace{0.05cm}'(k) \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| − | V_a\hspace{0.05cm}(k) = [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.05cm}.</math> | + | V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.05cm}.</math> |
| − | Wilhelm | + | Wilhelm refers to this representation as the $\rm L–model$, see [Wil11]<ref name='Wil11'>Wilhelm, C.: A-Model and L-Model, New Channel Models with Formulas for Probabilities of Error Structures. [http://www.channels-networks.net/ Internet Publication to Channels-Networks,] 2011ff.</ref>. The constant $\beta$ depends on |
| − | * | + | *the symbol error probability $p_{\rm S}$, and<br> |
| − | |||
| + | *the empirically found exponent $\alpha$ ⇒ burst factor $1- \alpha$, | ||
| − | + | ||
| + | such that the block error probability becomes equal to $1$ at infinite block length: | ||
::<math>\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_B(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) | ::<math>\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_B(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) | ||
| − | = p_{\rm S} \cdot \sum_{k = 1}^{n} [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)} | + | = p_{\rm S} \cdot \sum_{k = 1}^{n} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} |
=1 | =1 | ||
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sum_{k = 1}^{\infty} [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)} | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sum_{k = 1}^{\infty} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} |
= {1}/{p_{\rm S}} | = {1}/{p_{\rm S}} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | To determine $\beta$, we use the [https://en.wikipedia.org/wiki/Generating_function "generating function"] of ${V_a}(k)$, which we denote by ${V_a}(z)$: | |
::<math>V_a\hspace{0.05cm}(z) = \sum_{k = 1}^{\infty}V_a\hspace{0.05cm}(k) \cdot z^k = | ::<math>V_a\hspace{0.05cm}(z) = \sum_{k = 1}^{\infty}V_a\hspace{0.05cm}(k) \cdot z^k = | ||
| − | \sum_{k = 1}^{n} [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)} | + | \sum_{k = 1}^{n} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} |
\cdot z^k | \cdot z^k | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | In [Wil11]<ref name='Wil11'></ref> | + | In [Wil11]<ref name='Wil11'>Wilhelm, C.: A-Model and L-Model, New Channel Models with Formulas for Probabilities of Error Structures. [http://www.channels-networks.net/ Internet Publication to Channels-Networks,] 2011ff.</ref>, $V_a\hspace{0.05cm}(z) = 1/{\left (1- {\rm e}^{- \beta }\cdot z \right )^\alpha} |
| − | + | $ is derived approximately. From the equation for the mean error distance follows: | |
| − | ::<math> {\rm E}[a] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = \sum_{k = 1}^{\infty} V_a(k) = \sum_{k = 1}^{\infty} V_a(k) \cdot 1^k = V_a(z=1) = | + | ::<math> {\rm E}\big[a\big] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = \sum_{k = 1}^{\infty} V_a(k) = \sum_{k = 1}^{\infty} V_a(k) \cdot 1^k = V_a(z=1) = |
1/p_{\rm S}</math> | 1/p_{\rm S}</math> | ||
| − | ::<math> \Rightarrow \hspace{0.3cm}{p_{\rm S}} = \ | + | ::<math> \Rightarrow \hspace{0.3cm}{p_{\rm S}} = \big [V_a(z=1)\big]^{-1}= |
| − | \ | + | \big [1- {\rm e}^{- \beta }\cdot 1\big]^{\alpha}\hspace{0.3cm} |
\Rightarrow \hspace{0.3cm} | \Rightarrow \hspace{0.3cm} | ||
{\rm e}^{- \beta } =1 - {p_{\rm S}}^{1/\alpha}\hspace{0.05cm}.</math> | {\rm e}^{- \beta } =1 - {p_{\rm S}}^{1/\alpha}\hspace{0.05cm}.</math> | ||
| − | == | + | == Numerical comparison of the BSC model and the Wilhelm model== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ Let us summarize this intermediate result. Wilhelm's $\rm L–model$ describes the error distance distribution $\rm (EDD)$ in the form |
| − | ::<math>V_a\hspace{0.05cm}(k) = \ | + | ::<math>V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha}\big ] \cdot |
| − | \ | + | \big [ 1 - {p_{\rm S}^{1/\alpha} }\big ]^{k-1} |
\hspace{0.05cm}.</math>}} | \hspace{0.05cm}.</math>}} | ||
| − | + | This model will now be explained with exemplary numerical results and compared with the BSC model.<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6:}$ We start with the [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)#Binary_Symmetric_Channel_.E2.80.93_Model_and_Error_Correlation_Function|"BSC model"]]. |
| + | [[File:EN_Dig_T_5_3_S5h_ganz_neu.png|right|frame|BSC model and parameters for $p_{\rm S} = 0.2$|class=fit]] | ||
| + | |||
| + | #For presentation reasons, we set the falsification probability very high to $p_{\rm S} = 0.2$. | ||
| + | #In the second row of the table, its error distance distribution ${V_a}(k) = {\rm Pr}(a \ge k)$ is entered for $k \le 10$.<br> | ||
| − | |||
| − | + | The Wilhelm model with $p_{\rm S} = 0.2$ and $\alpha = 1$ has exactly the same error distance distribution as the corresponding [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)#Binary_Symmetric_Channel_.E2.80.93_Error_Distance_Distribution| "BSC model"]]. This is also shown by the calculation. | |
| − | ::<math>V_a\hspace{0.05cm}(k) = \ | + | With $\alpha = 1$ one obtains from the equation in the last section: |
| − | \ | + | |
| + | ::<math>V_a\hspace{0.05cm}(k) \hspace{-0.05cm}=\hspace{-0.05cm} \big [k^{\alpha}-(k-1)^{\alpha}\big ] \hspace{-0.05cm} \cdot \hspace{-0.05cm} | ||
| + | \big [ 1 - {p_{\rm S}^{1/\alpha} }\big ]^{k-1} \hspace{-0.1cm} = \hspace{-0.1cm} (1 - p_{\rm S} )^{k-1} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Thus, according to the lines '''3''' and '''4''', both models also have | |
| − | * | + | *equal error distance probabilities ${\rm Pr}(a = k)= {V_a}(k-1) - {V_a}(k)$,<br> |
| − | * | + | *equal block error probabilities $ p_{\rm B}(n)$.<br><br> |
| − | + | With regard to the following $\text{Example 7}$ with $\alpha \ne 1$, it should be mentioned again in particular: | |
| − | * | + | *The block error probabilities $ p_{\rm B}(n)$ of the Wilhelm model are basically obtained from the error distance distribution ${V_a}(k)$ according to the equation |
::<math> p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) | ::<math> p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) | ||
| Line 416: | Line 473: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Only in the special case $\alpha = 1$ ⇒ BSC model, $ p_{\rm B}(n)$ can also be determined by summation over the error distance probabilities ${\rm Pr}(a=k)$: |
::<math> p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} {\rm Pr}(a=k) | ::<math> p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} {\rm Pr}(a=k) | ||
| Line 424: | Line 481: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
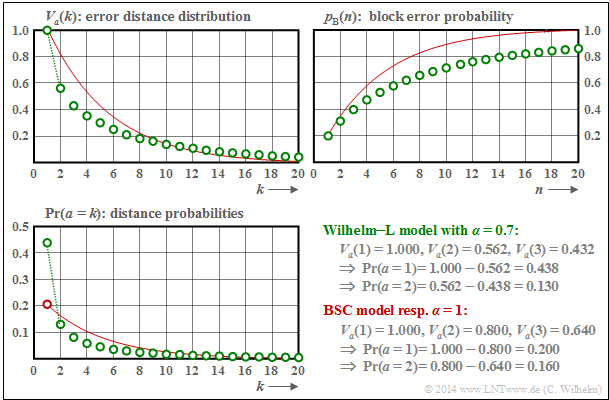
| − | $\text{ | + | $\text{Example 7:}$ We now consider a channel with burst error characteristics. |
| + | [[File:EN_Dig_T_5_3_S5h_ganz_neu.png|right|frame|Results of the Wilhelm-L model with $\alpha = 0.7$ and $p_{\rm S} = 0.2$<br><br> |class=fit]] | ||
| − | + | #The graph shows as green circles the results for the Wilhelm–L model with $\alpha = 0.7$. | |
| + | #The red comparison curve is valid for $\alpha = 1$ (or for the BSC channel) with the same mean symbol error probability $p_{\rm S} = 0.2$. | ||
| + | #Some interesting numerical values are given at the bottom right.<br> | ||
| − | |||
| − | |||
| − | * | + | One can see from these plots: |
| + | *The course of the block error probability starts with $p_{\rm B}(n = 1) = p_{\rm S} = 0.2$, both for statistically independent errors ("BSC") and for burst errors ("Wilhelm").<br> | ||
| − | * | + | *For the (green) burst error model, ${\rm Pr}(a=1)= 0.438$ is significantly larger than for the (red) BSC: ${\rm Pr}(a=1)= 0.2$. In addition, one can see a bent shape in the lower region.<br> |
| − | * | + | *However, the mean error distance ${\rm E}\big [a \big ] = 1/p_{\rm S} = 5$ is identical for both models with same symbol error probability. |
| + | *The large outlier at $k=1$ is compensated by smaller probabilities for $k=2$, $k=3$ ... as well as by the fact that for large $k$ the green circles lie – even if only minimally – above the red comparison curve.<br> | ||
| − | == | + | *The most important result is that the block error probability for $n > 1$ is smaller for the Wilhelm model than for the comparable BSC model, for example: $p_{\rm B}(n = 20) = 0.859$.}}<br> |
| + | |||
| + | |||
| + | == Error distance consideration according to the Wilhelm A model == | ||
<br> | <br> | ||
| − | + | Wilhelm has developed another approximation from the [https://en.wikipedia.org/wiki/Generating_function "generating function"] $V_a(z)$ given above, which he calls the "A model". The approximation is based on a Taylor series expansion.<br> | |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Wilhelm's $\text{A model}$ describes the approximated error distance distribution $\rm (EDD)$ in the form |
::<math>V_a\hspace{0.05cm}(k) = \frac {1 \cdot \alpha \cdot (1+\alpha) \cdot \hspace{0.05cm} ... \hspace{0.05cm}\cdot (k-2+\alpha) }{(k-1)\hspace{0.05cm}!}\cdot | ::<math>V_a\hspace{0.05cm}(k) = \frac {1 \cdot \alpha \cdot (1+\alpha) \cdot \hspace{0.05cm} ... \hspace{0.05cm}\cdot (k-2+\alpha) }{(k-1)\hspace{0.05cm}!}\cdot | ||
| Line 451: | Line 512: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *In particular, $V_a(k = 1) = 1$ and $V_a(k = 2)= \alpha \cdot (1 - p_{\rm S}^{1/\alpha})$ results. | |
| − | + | *It should be noted here that the numerator of the prefactor consists of $k$ factors. Consequently, for $k = 1$, this prefactor results in $1$.}}<br> | |
| + | |||
| + | Now we compare the differences of the two Wilhelm models $\rm(L$ and $\rm A)$, with respect to resulting block error probability. | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 8:}$ The adjacent graph shows the course of the block error probabilities $p_{\rm B}(n)$ for three different $\alpha$–values, recognizable by the colors |
| − | * | + | [[File:EN_Dig_T_5_3_S5m.png|right|frame||Wilhelm model results $(p_{\rm S} = 0.01)$ <br><br>]] |
| − | * | + | |
| − | * | + | *Red: $\alpha = 1.0$ ⇒ BSC model,<br> |
| + | *Blue: $\alpha = 0.95$ ⇒ weak bursting,<br> | ||
| + | *Green: $\alpha = 0.70$ ⇒ strong bursting.<br><br> | ||
| − | + | The solid lines apply to the "A model" and the dashed lines to the "L model". The numerical values for $p_{\rm B}(n = 100)$ given in the figure refer to the "A model".<br> | |
| − | + | For $\alpha = 1$, both the A model and the L model transition to the BSC model (red curve). | |
| − | |||
| − | + | Furthermore, it should be noted: | |
| + | #The symbol error probability $p_{\rm S} = 0.01$ ⇒ ${\rm E}\big[a \big ] = 100$ is assumed here $($reasonably$)$ realistic. All curves start at $p_{\rm B}(n=1) = 0.01$ ⇒ yellow point.<br> | ||
| + | #The difference between two curves of the same color is small $($somewhat larger in the case of strong bursting$)$, with the solid curve always lying above the dashed curve.<br> | ||
| + | #This example also shows: The stronger the bursting $($smaller $\alpha)$, the smaller the block error probability $p_{\rm B}(n)$. However, this is only true if one assumes as here a constant symbol error probability $p_{\rm S}$.<br> | ||
| + | #A (poor) attempt at an explanation: Suppose that for BSC with small $p_{\rm S}$ each block error comes from one symbol error, then for the same symbol errors there are fewer block errors if two errors fall into one block. | ||
| + | #Another (more appropriate?) example from everyday life. It is easier to cross a street with constant traffic volume, if the vehicles come "somehow bursted".}}<br> | ||
| − | + | == Error correlation function of the Wilhelm A model == | |
| + | <br> | ||
| + | In addition to the error distance distribution $V_a(k)$, another form of description of the digital channel models is the [[Digital_Signal_Transmission/Parameters_of_Digital_Channel_Models#Error_correlation_function|"error correlation function"]] $\rm (ECF$ $\varphi_{e}(k)$. We assume the binary error sequence $\langle e_\nu \rangle$ ⇒ $e_\nu \in \{0, 1\}$, where with respect to the $\nu$–th bit | ||
| + | *$e_\nu = 0$ denotes a correct transmission, and | ||
| − | * | + | *$e_\nu = 1$ a bit error. |
| − | |||
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ | |
| − | + | The '''error correlation function''' $\varphi_{e}(k)$ gives the $($discrete-time$)$ [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Auto-correlation_function_for_stationary_and_ergodic_processes|"auto-correlation function"]] of the random variable $e$, which is also discrete-time. | |
| − | |||
| − | |||
| − | ::<math>\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] = | + | ::<math>\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big] = |
| − | \overline{e_{\nu} \cdot e_{\nu + k}}\hspace{0.05cm}.</math> | + | \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.</math> |
| − | + | *The sweeping line in the right equation marks the time averaging.}} | |
| − | + | The error correlation value $\varphi_{e}(k)$ provides statistical information about two sequence elements that are $k$ apart, e.g. about $e_{\nu}$ and $e_{\nu +k}$. The intervening elements $e_{\nu +1}$, ... , $e_{\nu +k-1}$, on the other hand, do not affect the $\varphi_{e}(k)$ value.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Without proof:}$ The error correlation function of the $\text{Wilhelm A model}$ can be approximated as follows: |
| − | :<math>\varphi_e\hspace{0.05cm}(k) = p_{\rm S} \hspace{-0.03cm}\cdot \hspace{-0.03cm} \left [ 1 \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha}{1\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha \cdot (1\hspace{-0.03cm}-\hspace{-0.03cm} \alpha)}{2\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^2 \hspace{-0.03cm}-\hspace{-0.03cm} \hspace{0. | + | ::<math>\varphi_e\hspace{0.05cm}(k) = p_{\rm S} \hspace{-0.03cm}\cdot \hspace{-0.03cm} \left [ 1 \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha}{1\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha \cdot (1\hspace{-0.03cm}-\hspace{-0.03cm} \alpha)}{2\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^2 \hspace{-0.03cm}-\hspace{-0.03cm} \hspace{0.05cm} \text{...} \hspace{0.05cm}\hspace{-0.03cm}-\hspace{-0.03cm} \frac {\alpha \hspace{-0.03cm}\cdot \hspace{-0.03cm} (1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) \hspace{-0.03cm}\cdot \hspace{-0.03cm} \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{-0.03cm}\cdot \hspace{-0.03cm} (k\hspace{-0.03cm}-\hspace{-0.03cm}1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) }{k\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^k \right ] </math> |
| − | + | *Here, $C = (1-p_{\rm S})^{1/\alpha}$ is used for abbreviation. The derivation is omitted here.}}<br> | |
| − | + | In the following, the properties of the error correlation function are shown by an example.<br> | |
| − | + | {{GraueBox|TEXT= | |
| − | {{GraueBox|TEXT= | + | $\text{Example 9:}$ |
| − | $\text{ | + | As in [[Digital_Signal_Transmission/Burst_Error_Channels#Error_distance_consideration_according_to_the_Wilhelm_A_model| $\text{Example 8}$]]: $p_{\rm S} = 0.01$. The error correlation functions shown here again represent |
| − | + | [[File:EN_Dig_T_5_3_S5korr_version3.png|right|frame||ECF results of the Wilhelm model]] | |
| − | |||
| − | |||
| − | |||
| + | *Red: $\alpha = 1.0$ ⇒ BSC model,<br> | ||
| + | *Blue: $\alpha = 0.95$ ⇒ weak bursting,<br> | ||
| + | *Green: $\alpha = 0.70$ ⇒ strong bursting.<br><br> | ||
| − | + | The following statements can be generalized to a large extent, see also [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)#Binary_Symmetric_Channel_.E2.80.93_Model_and_Error_Correlation_Function|"Gilbert-Elliott model"]]: | |
| − | * | + | *The ECF value at $k = 0$ is equal to $p_{\rm S} = 10^{-2}$ for all channels $($marked by the circle with gray filling$)$ and the limit value for $k \to \infty$ is always $p_{\rm S}^2 = 10^{-4}$.<br> |
| − | * | + | *In the BSC model, this final value is already reached at $k = 1$ $($marked by a red filled circle$)$. Therefore, the ECF can only assume here the two values $p_{\rm S}$ and $p_{\rm S}^2$. <br> |
| − | * | + | *Also for $\alpha < 1$ $($blue and green curves$)$, a fold can be seen at $k = 1$. After that, the ECF is monotonically decreasing. The decrease is the slower, the smaller $\alpha$ is, i.e. the more bursted the errors occur.}}<br> |
| − | == | + | == Analysis of error structures with the Wilhelm A model== |
<br> | <br> | ||
| − | Wilhelm | + | Wilhelm developed his channel model mainly in order to be able to draw conclusions about the errors occurring from measured error sequences. From the multitude of analyses in [Wil11]<ref name='Wil11'>Wilhelm, C.: A-Model and L-Model, New Channel Models with Formulas for Probabilities of Error Structures. [http://www.channels-networks.net/ Internet Publication to Channels-Networks,] 2011ff.</ref> only a few are to be quoted here, whereby always the symbol error probability $p_{\rm S} = 10^{-3}$ is the basis. |
| + | *In the diagrams, the red curve applies in each case to statistically independent errors $($BSC or $\alpha = 1)$, | ||
| + | |||
| + | *the green curve for a burst error channel with $\alpha = 0.7$. In addition, the following agreement shall apply:<br> | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ An "'''error burst'''" $($or "burst" for short$)$ always starts with a symbol error and ends when $k_{\rm Burst}- 1$ error-free symbols follow each other. |
| − | *$k_{\rm Burst}$ | + | *$k_{\rm Burst}$ denotes the "burst end parameter". |
| − | * | + | |
| − | * | + | *The "burst weight" $G_{\rm Burst}$ corresponds to the number of all symbol errors in the burst. |
| + | |||
| + | *For a "single error", $G_{\rm Burst}= 1$ and the "burst length" (determined by the first and last error) is also $L_{\rm Burst}= 1$.}}<br> | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | [[File:EN_Dig_T_5_3_S5k.png|right|frame|Probability of a single error in a block of length $n$]] | ||
| + | |||
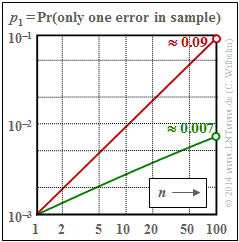
| + | $\text{Example 10:}\ \text{Probability }p_1\text{ of a single error in a sample of length} \ n$ | ||
| + | |||
| + | For the BSC channel $(\alpha = 1)$, $p_1 = n \cdot 0.001 \cdot 0.999^{n-1}$ ⇒ red curve. | ||
| + | *Due to the double-logarithmic representation, these numerical values result in a (nearly) linear progression. | ||
| + | |||
| + | *Thus, with the BSC model, single errors occur in a sample of length $n = 100$ with about $9\%$ probability.<br> | ||
| + | |||
| + | |||
| + | In the case of the burst error channel with $\alpha = 0.7$ ⇒ green curve, the corresponding probability is only about $0.7\%$ and the course of the curve is slightly curved here. | ||
| − | |||
| − | |||
| − | |||
| − | + | In the following calculation, we first assume that the single error in the sample of length $n$ occurs at position $b$: | |
| − | + | *Thus, in the case of a single error, $n-b$ error-free symbols must then follow. | |
| − | * | + | *After averaging over the possible error positions $b$, we thus obtain: |
::<math>p_1 = p_{\rm S} \cdot \sum_{b = 1}^{n} \hspace{0.15cm}V_a (b) \cdot V_a (n+1-b) | ::<math>p_1 = p_{\rm S} \cdot \sum_{b = 1}^{n} \hspace{0.15cm}V_a (b) \cdot V_a (n+1-b) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Because of its similarity to the signal representation of a [[Theory_of_Stochastic_Signals/Digital_Filters|"digital filter"]], the sum can be called "a convolution of $V_a(b)$ with itself". |
| − | + | *For the generating function $V_a(z)$, the convolution becomes a product $[$or the square because of $V_a(b) \star V_a(b)]$ and the following equation is obtained: | |
| − | |||
| − | * | + | ::<math>V_a(z=1) \cdot V_a(z=1) = \big [ V_a(z=1) \big ]^2 = |
| + | {\big [ 1 -(1- {p_{\rm S} }^{1/\alpha})\big ]^{-2\alpha} } \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Thus, with the [[Digital_Signal_Transmission/Burst_Error_Channels#Error_distance_consideration_to_the_Wilhelm_model|"specific error distance distribution"]] $V_a(z)$, we obtain the following final result: | ||
::<math>p_1 = p_{\rm S} | ::<math>p_1 = p_{\rm S} | ||
| Line 548: | Line 634: | ||
(1- {p_{\rm S} }^{1/\alpha})^{n-1} \hspace{0.05cm}.</math>}}<br> | (1- {p_{\rm S} }^{1/\alpha})^{n-1} \hspace{0.05cm}.</math>}}<br> | ||
| + | {{GraueBox|TEXT= | ||
| + | [[File:EN_Dig_T_5_3_S5l.png|right|frame|Mean number of errors in the burst of length $k$]] | ||
| + | |||
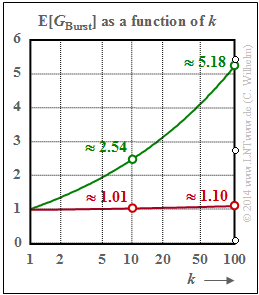
| + | $\text{Example 11:}\ \text{Mean number of errors } {\rm E}[G_{\rm Burst}] \text{ in a burst with end parameter }k_{\rm Burst}$ | ||
| − | + | Let the mean symbol error probability still be $p_{\rm S} = 10^{-3}$, i.e. (relatively) small.<br> | |
| − | |||
| − | $ | ||
| − | + | '''(A) Red curve for the BSC channel''' (or $\alpha = 1)$: | |
| + | # For example, the parameter $k_{\rm Burst}= 10$ means that the burst is finished when nine error-free symbols follow after one error. The probability for an error distance $a \le 9$ is extremely small when $p_{\rm S}$ is small $($here: $10^{-3})$. It further follows that then (almost) every single error is taken as a "burst", and ${\rm E}[G_{\rm Burst}] \approx 1.01$ .<br> | ||
| + | # If the burst end parameter $k_{\rm Burst}$ is larger, the probability ${\rm Pr}(a \le k_{\rm Burst})$ also increases significantly and "bursts" with more than one error occur. For example, if $k_{\rm Burst}= 100$ is chosen, a "burst" contains on average $1.1$ symbol errors.<br> | ||
| + | #This means at the same time, that long error bursts $($according to our definition$)$ can also occur in the BSC model if, for a given $p_{\rm S}$, the burst end parameter is chosen too large or, for a given $k_{\rm Burst}$, the mean error probability $p_{\rm S}$ is too large.<br><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(B) Green curve for the Wilhelm channel''' with $\alpha = 0.7$: |
| − | |||
| − | + | The procedure given here for the numerical determination of the mean error number ${\rm E}[G_{\rm Burst}]$ of a burst can be applied independently of the $\alpha$–value. One proceeds as follows: | |
| − | |||
| − | |||
| − | |||
| − | + | #According to the error distance probabilities ${\rm Pr}(a=k)$ one generates an error sequence $\langle e_1,\ e_2,\ \text{...} ,\ e_i\rangle$, ... with the error distances $a_1$, $a_2$, ... , $a_i$, ... <br> | |
| + | #If an error distance $a_i \ge k_{\rm Burst}$, this marks the end of a burst. Such an event occurs with probability ${\rm Pr}(a \ge k_{\rm Burst}) = V_a(k_{\rm Burst} )$. <br> | ||
| + | #We count such events "$a_i \ge k_{\rm Burst}$" in the entire block of length $n$. Their number is simultaneously the number of bursts $(N_{\rm Burst})$ in the block. <br> | ||
| + | #At the same time, the relation $N_{\rm Burst} = N_{\rm error} \cdot V_a(k_{\rm Burst} )$ holds, where $N_{\rm error}$ is the number of all errors in the block. | ||
| + | #From this, the average number of errors per burst can be calculated in a simple way: | ||
| − | + | :::<math>{\rm E}[G_{\rm Burst}] =\frac {N_{\rm error} }{N_{\rm Burst} } =\frac {1}{V_a(k_{\rm Burst})}\hspace{0.05cm}.</math> | |
| − | |||
| − | |||
| − | == | + | The markings in the graph correspond to the following numerical values of the [[Digital_Signal_Transmission/Burst_Error_Channels#Error_distance_consideration_to_the_Wilhelm_model|"error distance distribution"]]: |
| + | *The green circles $($Wilhelm channel, $\alpha = 0.7)$ result from $V_a(10) = 0.394$ and $V_a(100) = 0.193$. | ||
| + | |||
| + | *The red circles $($BSC channel, $\alpha = 1)$ are the reciprocals of $V_a(10) = 0.991$ and $V_a(100) = 0906$.}}<br> | ||
| + | |||
| + | == Exercises for the chapter == | ||
<br> | <br> | ||
| − | [[Aufgaben:5.6 | + | [[Aufgaben:Exercise_5.6:_Error_Correlation_Duration|Exercise 5.6: Error Correlation Duration]] |
| + | |||
| + | [[Aufgaben:Exercise_5.6Z:_Gilbert-Elliott_Model|Exercise 5.6Z: Gilbert-Elliott Model]] | ||
| + | |||
| + | [[Aufgaben:Exercise_5.7:_McCullough_and_Gilbert-Elliott_Parameters|Exercise 5.7: McCullough and Gilbert-Elliott Parameters]] | ||
| + | |||
| + | [[Aufgaben:Exercise_5.7Z:_McCullough_Model_once_more|Exercise 5.7Z: McCullough Model once more]] | ||
| − | |||
| − | |||
| − | |||
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 17:10, 24 October 2022
Contents
- 1 Channel model according to Gilbert-Elliott
- 2 Error distance distribution of the Gilbert-Elliott model
- 3 Error correlation function of the Gilbert-Elliott model
- 4 Channel model according to McCullough
- 5 Conversion of the GE parameters into the MC parameters
- 6 Burst error channel model according to Wilhelm
- 7 Error distance consideration to the Wilhelm model
- 8 Numerical comparison of the BSC model and the Wilhelm model
- 9 Error distance consideration according to the Wilhelm A model
- 10 Error correlation function of the Wilhelm A model
- 11 Analysis of error structures with the Wilhelm A model
- 12 Exercises for the chapter
- 13 References
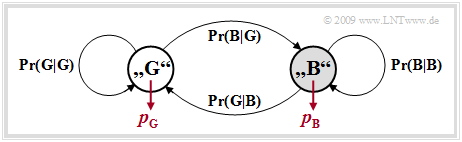
Channel model according to Gilbert-Elliott
This channel model, which goes back to E. N. Gilbert [Gil60][1] and E. O. Elliott [Ell63][2], is suitable for describing and simulating "digital transmission systems with burst error characteristics".
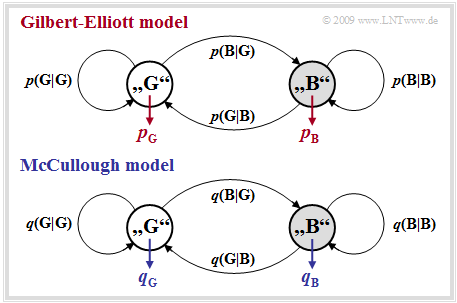
The Gilbert–Elliott model $($abbreviation: "GE model"$)$ can be characterized as follows:
- The different transmission quality at different times is expressed by a finite number $g$ of channel states $(Z_1, Z_2,\hspace{0.05cm} \text{...} \hspace{0.05cm}, Z_g)$.
- The in reality smooth transitions of the interference intensity – in the extreme case from completely error-free transmission to total failure – are approximated in the GE model by fixed probabilities in the individual channel states.
- The transitions between the $g$ states occur according to a "Markov process" (1st order) and are characterized by $g \cdot (g-1)$ transition probabilities. Together with the $g$ error probabilities in the individual states, there are thus $g^2$ free model parameters.
- For reasons of mathematical manageability, one usually restricts oneself to $g = 2$ states and denotes these with $\rm G$ ("GOOD") and $\rm B$ ("BAD"). Mostly, the error probability in state $\rm G$ will be much smaller than in state $\rm B$.
- In that what follows, we use these two error probabilities $p_{\rm G}$ and $p_{\rm B}$, where $p_{\rm G} < p_{\rm B}$ should hold, as well as the transition probabilities ${\rm Pr}({\rm B}\hspace{0.05cm}|\hspace{0.05cm}{\rm G})$ and ${\rm Pr}({\rm G}\hspace{0.05cm}|\hspace{0.05cm}{\rm B})$. This also determines the other two transition probabilities:
- \[{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) = 1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G), \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B) = 1 - {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{0.05cm}.\]
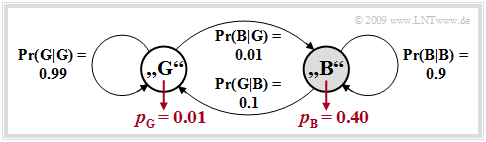
$\text{Example 1:}$ We consider the Gilbert-Elliott model with the parameters
- $$p_{\rm G} = 0.01,$$
- $$p_{\rm B} = 0.4,$$
- $${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) = 0.1, $$
- $$ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
The underlying model is shown at the end of this example with the parameters given here.
The upper graphic shows a (possible) error sequence of length $N = 800$. If the GE model is in the "BAD" state, this is indicated by the gray background.
To simulate such a GE error sequence, switching is performed between the states "GOOD" and "BAD" according to the four transition probabilities.
- At the first clock call, the selection of the state is expediently done according to the "state probabilities" $w_{\rm G}$ and $w_{\rm B}$, as calculated below.
- At each clock cycle, exactly one element of the error sequence $ \langle e_\nu \rangle$ is generated according to the current error probability $(p_{\rm G}$ or $p_{\rm B})$.
- The "error distance simulation" is not applicable here, because in the GE model a state change is possible after each symbol $($and not only after an error$)$.
The probabilities that the Markov chain is in the "GOOD" or "BAD" state can be calculated from the assumed homogeneity and stationarity.
One obtains with the above numerical values:
- \[w_{\rm G} = {\rm Pr(in\hspace{0.15cm} state \hspace{0.15cm}G)}= \frac{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B)}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01} = {10}/{11}\hspace{0.05cm},\]
- \[w_{\rm B} = {\rm Pr(in\hspace{0.15cm} state \hspace{0.15cm}B)}= \frac{ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)} = \frac{0.11}{0.1 + 0.01} = {1}/{11}\hspace{0.05cm}.\]
These two state probabilities can also be used to determine the "mean error probability" of the GE model:
- \[p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \frac{p_{\rm G} \cdot {\rm Pr}({\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B)}+ p_{\rm B} \cdot {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G)} \hspace{0.05cm}.\]
In particular, for the model considered here as an example:
- \[p_{\rm M} ={10}/{11} \cdot 0.01 +{1}/{11} \cdot 0.4 = {1}/{22} \approx 4.55\%\hspace{0.05cm}.\]
Error distance distribution of the Gilbert-Elliott model
In [Hub82][3] you can find the analytical computations
- of the "probability of the error distance $k$":
- \[{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm G}) + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm B})\hspace{0.05cm},\]
- the "error distance distribution" $\rm (EDD)$:
- \[V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.\]
The following auxiliary quantities are used here:
- \[u_{\rm GG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\]
- \[u_{\rm BB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}\]
- \[\Rightarrow \hspace{0.3cm} \beta_{\rm G} =\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},\]
- \[\hspace{0.8cm}\beta_{\rm B} =\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]
- \[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}\]
- \[\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]
The given equations are the result of extensive matrix operations.
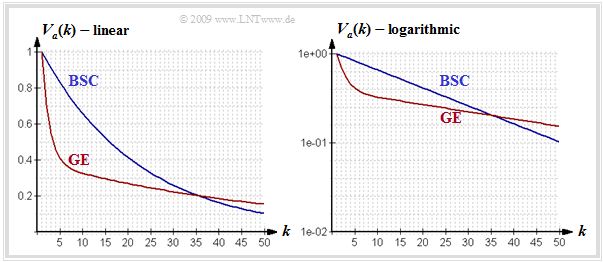
The upper graph shows the error distance distribution $\rm (EDD)$ of the Gilbert-Elliott model (red curve) in linear and logarithmic representation for the parameters
- $${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = 0.1 \hspace{0.05cm},\hspace{0.5cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) = 0.01 \hspace{0.05cm},\hspace{0.5cm}p_{\rm G} = 0.001, \hspace{0.5cm}p_{\rm B} = 0.4.$$
For comparison, the corresponding $V_a(k)$ curve for the BSC model with the same mean error probability $p_{\rm M} = 4.5\%$ is also plotted as blue curve.
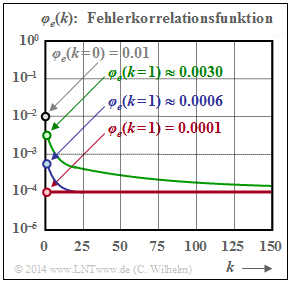
Error correlation function of the Gilbert-Elliott model
For the "error correlation function" $\rm (ECF)$ of the GE model with
- the mean error probability $p_{\rm M}$,
- the transition probabilities ${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )$ and ${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )$ as well as
- the error probabilities $p_{\rm G}$ and $p_{\rm B}$ in the two states $\rm G$ and $\rm B$,
we obtain after extensive matrix operations the relatively simple expression
- \[\varphi_{e}(k) = {\rm E}\big[e_\nu \cdot e_{\nu +k}\big] = \left\{ \begin{array}{c} p_{\rm M} \\ p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) (p_{\rm M} - p_{\rm G}) [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^k \end{array} \right.\quad \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}\]
For the Gilbert-Elliott model, for "renewing models" $\varphi_{e}(k)$ must always be calculated according to this equation. The iterative calculation algorithm for "renewing models",
- $$\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa), $$
cannot be applied here, since the GE model is not renewing ⇒ here, the error distances are not statistically independent of each other.
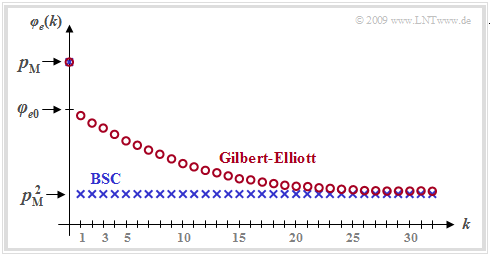
The graph shows an example of the ECF curve of the Gilbert-Elliott model marked with red circles. One can see from this representation:
- While for the memoryless channel $($BSC model, blue curve$)$ all ECF values are $\varphi_{e}(k \ne 0)= p_{\rm M}^2$, the ECF values approach this final value for the burst error channel much more slowly.
- At the transition from $k = 0$ to $k = 1$ a certain discontinuity occurs. While $\varphi_{e}(k = 0)= p_{\rm M}$, the second equation valid for $k > 0$ yields the following extrapolated value for $k = 0$:
- \[\varphi_{e0} = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G})\hspace{0.05cm}.\]
- A quantitative measure of the length of the statistical ties is the "correlation duration" $D_{\rm K}$, which is defined as the width of an equal-area rectangle of height $\varphi_{e0} - p_{\rm M}^2$:
- \[D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} \big[\varphi_{e}(k) - p_{\rm M}^2\big ]\hspace{0.05cm}.\]
$\text{Conclusions:}$ In the Gilbert–Elliott model, the "correlation duration" is given by the simple, analytically expressible expression
- \[D_{\rm K} =\frac{1}{ {\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G )}-1 \hspace{0.05cm}.\]
- $D_{\rm K}$ is larger the smaller ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G )$ and ${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ are, i.e., when state changes occur rarely.
- For the BSC model ⇒ $p_{\rm B}= p_{\rm G} = p_{\rm M}$ ⇒ $D_{\rm K} = 0$, this equation is not applicable.
Channel model according to McCullough
The main disadvantage of the Gilbert–Elliott model is that it does not allow error distance simulation. As will be worked out in "Exercise 5.5", this has great advantages over the symbol-wise generation of the error sequence $\langle e_\nu \rangle$ in terms of computational speed and memory requirements.
- McCullough [McC68][4] modified the model developed three years earlier by Gilbert and Elliott so
- that an error distance simulation in the two states "GOOD" and "BAD" is applicable in each case by itself.
The graph shows McCullough's model, hereafter referred to as the "MC model", while the "GE model" is shown above after renaming the transition probabilities ⇒ ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, ${\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) \rightarrow {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$, etc.
There are many similarities and a few differences between the two models:
- Like the Gilbert–Elliott model, the McCullough channel model is based on a "first-order Markov process" with the two states "GOOD" $(\rm G)$ and "BAD" $(\rm B)$. No difference can be found with respect to the model structure.
- The main difference to the Gilbert–Elliott is that a change of state between "GOOD" and "BAD" is only possible after an error – i.e. a "$1$" in the error sequence. This enables an "error distance simulation".
- The four freely selectable GE parameters $p_{\rm G}$, $p_{\rm B}$, ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$, ${\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ can be converted into the MC parameters $q_{\rm G}$, $q_{\rm B}$, ${\it q}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$, ${\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B )$ in such a way that an error sequence with the same statistical properties as in the GE model is generated. See next section.
- For example, ${\it q}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ denotes the transition probability from "GOOD" to "BAD" under the condition that an error has just occurred. The comparable GE parameter ${\it p}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G )$ characterizes this transition probability without this additional condition.
$\text{Example 2:}$ The figure above shows an exemplary error sequence of the Gilbert-Elliott model with the parameters
- $$p_{\rm G} = 0.01,$$
- $$p_{\rm B} = 0.4,$$
- $${\rm Pr}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm} B) = 0.1, $$
- $$ {\rm Pr}(\rm B\hspace{0.05cm}\vert\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
An error sequence of the equivalent McCullough model is drawn below. The relations between the two models can be summarized as follows:
- In the GE error sequence, a change from state "GOOD" (white background) to state "BAD" (gray background) and vice versa is possible at any time $\nu$, even when $e_\nu = 0$.
- In contrast, in the ML error sequence, a change of state at time $\nu$ is only possible at $e_\nu = 1$. The last error value before a gray background is always "$1$".
- With the ML model one does not have to generate the errors "step–by–step", but can use the faster error distance simulation ⇒ see "Exercise 5.5".
- The GE parameters can be converted into corresponding MC parameters in such a way that the two models are equivalent ⇒ see next section.
- That means: The MC error sequence has exactly same statistical properties as the GE sequence. But, it does not mean that both error sequences are identical.
Conversion of the GE parameters into the MC parameters
The parameters of the equivalent MC model can be calculated from the GE parameters as follows:
- $$q_{\rm G} =1-\beta_{\rm G}\hspace{0.05cm},$$
- $$ q_{\rm B} = 1-\beta_{\rm B}\hspace{0.05cm}, $$
- $$q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) =\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm},$$
- $$q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$
- Here again the following auxiliary quantities are used:
- \[u_{\rm GG} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\]
- \[u_{\rm BB} = {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\]
- \[\Rightarrow \hspace{0.3cm} \beta_{\rm G} = \frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm}, \hspace{0.9cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]
- \[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}} \Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.9cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]
$\text{Example 3:}$ As in $\text{Example 2}$, the GE parameters are:
- $$p_{\rm G} = 0.01, \hspace{0.5cm} p_{\rm B} = 0.4, \hspace{0.5cm} p(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.01, \hspace{0.5cm} {\it p}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.1.$$
Applying the above equations, we then obtain for the equivalent MC parameters:
- $$q_{\rm G} = 0.0186, \hspace{0.5cm} q_{\rm B} = 0.4613, \hspace{0.5cm} q(\rm B\hspace{0.05cm}\vert\hspace{0.05cm}G ) = 0.3602, \hspace{0.5cm} {\it q}(\rm G\hspace{0.05cm}\vert\hspace{0.05cm}B ) = 0.2240.$$
- If we compare in $\text{Example 2}$ the red error sequence $($GE, change of state is always possible$)$ with the blue sequence $($equivalent MC, change of state only at $e_\nu = 1$$)$, we can see quite serious differences.
- But the blue error sequence of the equivalent McCullough model has exactly the same statistical properties as the red error sequence of the Gilbert-Elliott model.
The conversion of the GE parameters to the MC parameters is illustrated in "Exercise 5.7" using a simple example. "Exercise 5.7Z" further shows how they can be determined directly from the $q$ parameters:
- the mean error probability,
- the error distance distribution,
- the error correlation function and
- the correlation duration of the MC model.
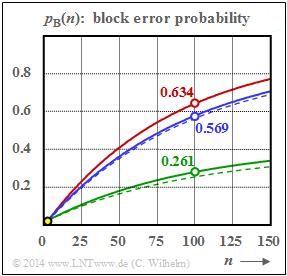
Burst error channel model according to Wilhelm
This model goes back to Claus Wilhelm and was developed from the mid-1960s onwards from empirical measurements of temporal consequences of bit errors.
- It is based on thousands of measurement hours in transmission channels from $\text{200 bit/s}$ with analog modem up to $\text{2.048 Mbit/s}$ via "ISDN".
- Likewise, marine radio channels up to $7500$ kilometers in the shortwave range were measured.
Blocks of length $n$ were recorded. The respective block error rate $h_{\rm B}(n)$ was determined from this. Note.
- A block error is already present if even one of the $n$ symbols has been falsified.
- Knowing well that the "block error rate" $h_{\rm B}(n)$ corresponds exactly to the "block error probability" $p_{\rm B}$ only for $n \to \infty$, we set $p_{\rm B}(n) \approx h_{\rm B}(n)$ in the following description.
- In another context, $p_{\rm B}$ sometimes also denotes the "bit error probability" in our learning tutorial.
In a large number of measurements, the fact that
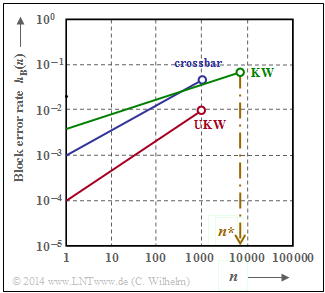
⇒ the course $p_{\rm B}(n)$ in double-logarithmic representation shows linear increases in the lower range
has been confirmed again and again $($see graph$)$. Thus, it holds for $n \le n^\star$:
- \[{\rm lg} \hspace{0.15cm}p_{\rm B}(n) = {\rm lg} \hspace{0.15cm}p_{\rm S} + \alpha \cdot {\rm lg} \hspace{0.15cm}n\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\hspace{0.05cm}.\]
- Here, $p_{\rm S} = p_{\rm B}(n=1)$ denotes the mean symbol error probability.
- The empirically found values of $\alpha$ are between $0.5$ and $0.95$.
- For $1-\alpha$, the term "burst factor" is also used.
$\text{Example 4:}$ In the BSC model, the course of the block error probability is:
- \[p_{\rm B}(n) =1 -(1 -p_{\rm S})^n \approx n \cdot p_{\rm S}\hspace{0.05cm}.\]
From this follows $\alpha = 1$ and the burst factor $1-\alpha = 0$. In this case $($and only in this case$)$ a linear course results even with non-logarithmic representation.
- Note that the above approximation is only valid for $p_{\rm S} \ll 1$ and not too large $n$, otherwise the approximation $(1-p_{\rm S})^n \approx1 - n \cdot p_{\rm S}$ is not applicable.
- But this also means that the equation given above is also only valid for a lower range $($for $n < n^\star)$.
- Otherwise, an infinitely large block error probability would result for $n \to \infty$.
$\text{Definition:}$ For the function $p_{\rm B}(n)$ ⇒ "block error probability" determined empirically from measurements, we now have to find the error distance distribution $\rm (EDD)$ from which the course for $n > n^\star$ can be extrapolated, which satisfies the following constraint:
- \[\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_{\rm B}(n) = 1 .\]
- We refer to this approach as the Wilhelm model.
- Since memory extends only to the last symbol error, this model is a renewal model.
Error distance consideration to the Wilhelm model
We now consider the error distances. An "error sequence" $\langle e_\nu \rangle$ can be equivalently represented by the "error distance sequence" $\langle a_{\nu\hspace{0.06cm}'} \rangle$, as shown in the following graph. It can be seen:
- The error sequence "$\text{...}\rm 1001\text{...}$" is expressed by "$a= 3$".
- Accordingly, the error distance "$a= 1$" denotes the error sequence "$\text{...}\rm 11\text{...}$".
- The different indices $\nu$ and $\nu\hspace{0.06cm}'$ take into account that the two sequences do not run synchronously.
With the probabilities $p_a(k) = {\rm Pr}(a= k)$ for the individual error distances $k$ and the mean symbol error probability $p_{\rm S}$, the following definitions apply for
- the "error distance distribution" $\rm (EDD)$:
- \[ V_a(k) = {\rm Pr}(a \ge k)= \sum_{\kappa = k}^{\infty}p_a(\kappa) \hspace{0.05cm},\]
- the "mean error distance" ${\rm E}\big[a\big]$:
- \[ V_a(k) = {\rm E}\big[a\big] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = {1}/{p_{\rm S}}\hspace{0.05cm}.\]
$\text{Example 5:}$ We consider a block with $n$ bits, starting at bit position $\nu + 1$.
Some comments:
- A block error occurs whenever a bit is falsified at positions $\nu + 1$, ... , $\nu + n$.
- The falsification probabilities are expressed in the graph by the error distance distribution ${V_a}\hspace{0.06cm}'(k)$.
- Somewhere before the block of length $n = 3$ is the last error, but at least at distance $k$ from the first error in the block.
- So the distance is equal or greater than $k$, which corresponds exactly to the probability ${V_a}'(k)$.
- The apostrophe is to indicate that a correction has to be made later to get from the empirically found error distance distribution to the correct function ${V_a}(k)$.
We now have several equations for the block error probability $p_{\rm B}(n)$.
- A first equation establishes the relationship between $p_{\rm B}(n)$ and the (approximate) error distance distribution ${V_a}'(k)$:
- \[(1)\hspace{0.4cm} p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) \hspace{0.05cm}, \]
- A second equation is provided by our empirical investigation at the beginning of this section:
- \[(2)\hspace{0.4cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\]
- The third equation is obtained by equating $(1)$ and $(2)$:
- \[(3)\hspace{0.4cm} \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) = n^{\alpha} \hspace{0.05cm}. \]
By successively substituting $n = 1, 2, 3,$ ... into this equation, we obtain with ${V_a}'(k = 1) = 1$:
- \[V_a\hspace{0.05cm}'(1) = 1^{\alpha} \hspace{0.05cm},\hspace{0.8cm} V_a\hspace{0.05cm}'(1) + V_a\hspace{0.05cm}'(2) =2^{\alpha} \hspace{0.05cm}, \hspace{0.8cm}V_a\hspace{0.05cm}'(1) + V_a\hspace{0.05cm}'(2) + V_a\hspace{0.05cm}'(3) = 3^{\alpha} \hspace{0.35cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}'(k) = k^{\alpha}-(k-1)^{\alpha} \hspace{0.05cm}.\]
However, the coefficients ${V_a}'(k)$ obtained from empirical data do not necessarily satisfy the normalization condition.
To correct the issue, Wilhelm uses the following approach:
- \[V_a\hspace{0.05cm}(k) = V_a\hspace{0.05cm}'(k) \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.05cm}.\]
Wilhelm refers to this representation as the $\rm L–model$, see [Wil11][5]. The constant $\beta$ depends on
- the symbol error probability $p_{\rm S}$, and
- the empirically found exponent $\alpha$ ⇒ burst factor $1- \alpha$,
such that the block error probability becomes equal to $1$ at infinite block length:
- \[\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_B(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) = p_{\rm S} \cdot \sum_{k = 1}^{n} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sum_{k = 1}^{\infty} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} = {1}/{p_{\rm S}} \hspace{0.05cm}.\]
To determine $\beta$, we use the "generating function" of ${V_a}(k)$, which we denote by ${V_a}(z)$:
- \[V_a\hspace{0.05cm}(z) = \sum_{k = 1}^{\infty}V_a\hspace{0.05cm}(k) \cdot z^k = \sum_{k = 1}^{n} \big [k^{\alpha}-(k-1)^{\alpha} \big ] \cdot {\rm e}^{- \beta \cdot (k-1)} \cdot z^k \hspace{0.05cm}.\]
In [Wil11][5], $V_a\hspace{0.05cm}(z) = 1/{\left (1- {\rm e}^{- \beta }\cdot z \right )^\alpha} $ is derived approximately. From the equation for the mean error distance follows:
- \[ {\rm E}\big[a\big] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = \sum_{k = 1}^{\infty} V_a(k) = \sum_{k = 1}^{\infty} V_a(k) \cdot 1^k = V_a(z=1) = 1/p_{\rm S}\]
- \[ \Rightarrow \hspace{0.3cm}{p_{\rm S}} = \big [V_a(z=1)\big]^{-1}= \big [1- {\rm e}^{- \beta }\cdot 1\big]^{\alpha}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm e}^{- \beta } =1 - {p_{\rm S}}^{1/\alpha}\hspace{0.05cm}.\]
Numerical comparison of the BSC model and the Wilhelm model
$\text{Conclusion:}$ Let us summarize this intermediate result. Wilhelm's $\rm L–model$ describes the error distance distribution $\rm (EDD)$ in the form
- \[V_a\hspace{0.05cm}(k) = \big [k^{\alpha}-(k-1)^{\alpha}\big ] \cdot \big [ 1 - {p_{\rm S}^{1/\alpha} }\big ]^{k-1} \hspace{0.05cm}.\]
This model will now be explained with exemplary numerical results and compared with the BSC model.
$\text{Example 6:}$ We start with the "BSC model".
- For presentation reasons, we set the falsification probability very high to $p_{\rm S} = 0.2$.
- In the second row of the table, its error distance distribution ${V_a}(k) = {\rm Pr}(a \ge k)$ is entered for $k \le 10$.
The Wilhelm model with $p_{\rm S} = 0.2$ and $\alpha = 1$ has exactly the same error distance distribution as the corresponding "BSC model". This is also shown by the calculation.
With $\alpha = 1$ one obtains from the equation in the last section:
- \[V_a\hspace{0.05cm}(k) \hspace{-0.05cm}=\hspace{-0.05cm} \big [k^{\alpha}-(k-1)^{\alpha}\big ] \hspace{-0.05cm} \cdot \hspace{-0.05cm} \big [ 1 - {p_{\rm S}^{1/\alpha} }\big ]^{k-1} \hspace{-0.1cm} = \hspace{-0.1cm} (1 - p_{\rm S} )^{k-1} \hspace{0.05cm}.\]
Thus, according to the lines 3 and 4, both models also have
- equal error distance probabilities ${\rm Pr}(a = k)= {V_a}(k-1) - {V_a}(k)$,
- equal block error probabilities $ p_{\rm B}(n)$.
With regard to the following $\text{Example 7}$ with $\alpha \ne 1$, it should be mentioned again in particular:
- The block error probabilities $ p_{\rm B}(n)$ of the Wilhelm model are basically obtained from the error distance distribution ${V_a}(k)$ according to the equation
- \[ p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} p_{\rm B}( 1) = 0.2 \cdot 1 = 0.2 \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B}(2) = 0.2 \cdot (1+0.8) = 0.36 \hspace{0.05cm}.\]
- Only in the special case $\alpha = 1$ ⇒ BSC model, $ p_{\rm B}(n)$ can also be determined by summation over the error distance probabilities ${\rm Pr}(a=k)$:
- \[ p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} {\rm Pr}(a=k) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} p_{\rm B}( 1) = 0.2 \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B}(2) = 0.2+ 0.16 = 0.36 \hspace{0.05cm}.\]
$\text{Example 7:}$ We now consider a channel with burst error characteristics.
- The graph shows as green circles the results for the Wilhelm–L model with $\alpha = 0.7$.
- The red comparison curve is valid for $\alpha = 1$ (or for the BSC channel) with the same mean symbol error probability $p_{\rm S} = 0.2$.
- Some interesting numerical values are given at the bottom right.
One can see from these plots:
- The course of the block error probability starts with $p_{\rm B}(n = 1) = p_{\rm S} = 0.2$, both for statistically independent errors ("BSC") and for burst errors ("Wilhelm").
- For the (green) burst error model, ${\rm Pr}(a=1)= 0.438$ is significantly larger than for the (red) BSC: ${\rm Pr}(a=1)= 0.2$. In addition, one can see a bent shape in the lower region.
- However, the mean error distance ${\rm E}\big [a \big ] = 1/p_{\rm S} = 5$ is identical for both models with same symbol error probability.
- The large outlier at $k=1$ is compensated by smaller probabilities for $k=2$, $k=3$ ... as well as by the fact that for large $k$ the green circles lie – even if only minimally – above the red comparison curve.
- The most important result is that the block error probability for $n > 1$ is smaller for the Wilhelm model than for the comparable BSC model, for example: $p_{\rm B}(n = 20) = 0.859$.
Error distance consideration according to the Wilhelm A model
Wilhelm has developed another approximation from the "generating function" $V_a(z)$ given above, which he calls the "A model". The approximation is based on a Taylor series expansion.
$\text{Definition:}$ Wilhelm's $\text{A model}$ describes the approximated error distance distribution $\rm (EDD)$ in the form
- \[V_a\hspace{0.05cm}(k) = \frac {1 \cdot \alpha \cdot (1+\alpha) \cdot \hspace{0.05cm} ... \hspace{0.05cm}\cdot (k-2+\alpha) }{(k-1)\hspace{0.05cm}!}\cdot \left [ 1 - {p_{\rm S}^{1/\alpha} }\right ]^{k-1} \hspace{0.05cm}.\]
- In particular, $V_a(k = 1) = 1$ and $V_a(k = 2)= \alpha \cdot (1 - p_{\rm S}^{1/\alpha})$ results.
- It should be noted here that the numerator of the prefactor consists of $k$ factors. Consequently, for $k = 1$, this prefactor results in $1$.
Now we compare the differences of the two Wilhelm models $\rm(L$ and $\rm A)$, with respect to resulting block error probability.
$\text{Example 8:}$ The adjacent graph shows the course of the block error probabilities $p_{\rm B}(n)$ for three different $\alpha$–values, recognizable by the colors
- Red: $\alpha = 1.0$ ⇒ BSC model,
- Blue: $\alpha = 0.95$ ⇒ weak bursting,
- Green: $\alpha = 0.70$ ⇒ strong bursting.
The solid lines apply to the "A model" and the dashed lines to the "L model". The numerical values for $p_{\rm B}(n = 100)$ given in the figure refer to the "A model".
For $\alpha = 1$, both the A model and the L model transition to the BSC model (red curve).
Furthermore, it should be noted:
- The symbol error probability $p_{\rm S} = 0.01$ ⇒ ${\rm E}\big[a \big ] = 100$ is assumed here $($reasonably$)$ realistic. All curves start at $p_{\rm B}(n=1) = 0.01$ ⇒ yellow point.
- The difference between two curves of the same color is small $($somewhat larger in the case of strong bursting$)$, with the solid curve always lying above the dashed curve.
- This example also shows: The stronger the bursting $($smaller $\alpha)$, the smaller the block error probability $p_{\rm B}(n)$. However, this is only true if one assumes as here a constant symbol error probability $p_{\rm S}$.
- A (poor) attempt at an explanation: Suppose that for BSC with small $p_{\rm S}$ each block error comes from one symbol error, then for the same symbol errors there are fewer block errors if two errors fall into one block.
- Another (more appropriate?) example from everyday life. It is easier to cross a street with constant traffic volume, if the vehicles come "somehow bursted".
Error correlation function of the Wilhelm A model
In addition to the error distance distribution $V_a(k)$, another form of description of the digital channel models is the "error correlation function" $\rm (ECF$ $\varphi_{e}(k)$. We assume the binary error sequence $\langle e_\nu \rangle$ ⇒ $e_\nu \in \{0, 1\}$, where with respect to the $\nu$–th bit
- $e_\nu = 0$ denotes a correct transmission, and
- $e_\nu = 1$ a bit error.
$\text{Definition:}$ The error correlation function $\varphi_{e}(k)$ gives the $($discrete-time$)$ "auto-correlation function" of the random variable $e$, which is also discrete-time.
- \[\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]
- The sweeping line in the right equation marks the time averaging.
The error correlation value $\varphi_{e}(k)$ provides statistical information about two sequence elements that are $k$ apart, e.g. about $e_{\nu}$ and $e_{\nu +k}$. The intervening elements $e_{\nu +1}$, ... , $e_{\nu +k-1}$, on the other hand, do not affect the $\varphi_{e}(k)$ value.
$\text{Without proof:}$ The error correlation function of the $\text{Wilhelm A model}$ can be approximated as follows:
- \[\varphi_e\hspace{0.05cm}(k) = p_{\rm S} \hspace{-0.03cm}\cdot \hspace{-0.03cm} \left [ 1 \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha}{1\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha \cdot (1\hspace{-0.03cm}-\hspace{-0.03cm} \alpha)}{2\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^2 \hspace{-0.03cm}-\hspace{-0.03cm} \hspace{0.05cm} \text{...} \hspace{0.05cm}\hspace{-0.03cm}-\hspace{-0.03cm} \frac {\alpha \hspace{-0.03cm}\cdot \hspace{-0.03cm} (1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) \hspace{-0.03cm}\cdot \hspace{-0.03cm} \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{-0.03cm}\cdot \hspace{-0.03cm} (k\hspace{-0.03cm}-\hspace{-0.03cm}1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) }{k\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^k \right ] \]
- Here, $C = (1-p_{\rm S})^{1/\alpha}$ is used for abbreviation. The derivation is omitted here.
In the following, the properties of the error correlation function are shown by an example.
$\text{Example 9:}$ As in $\text{Example 8}$: $p_{\rm S} = 0.01$. The error correlation functions shown here again represent
- Red: $\alpha = 1.0$ ⇒ BSC model,
- Blue: $\alpha = 0.95$ ⇒ weak bursting,
- Green: $\alpha = 0.70$ ⇒ strong bursting.
The following statements can be generalized to a large extent, see also "Gilbert-Elliott model":
- The ECF value at $k = 0$ is equal to $p_{\rm S} = 10^{-2}$ for all channels $($marked by the circle with gray filling$)$ and the limit value for $k \to \infty$ is always $p_{\rm S}^2 = 10^{-4}$.
- In the BSC model, this final value is already reached at $k = 1$ $($marked by a red filled circle$)$. Therefore, the ECF can only assume here the two values $p_{\rm S}$ and $p_{\rm S}^2$.
- Also for $\alpha < 1$ $($blue and green curves$)$, a fold can be seen at $k = 1$. After that, the ECF is monotonically decreasing. The decrease is the slower, the smaller $\alpha$ is, i.e. the more bursted the errors occur.
Analysis of error structures with the Wilhelm A model
Wilhelm developed his channel model mainly in order to be able to draw conclusions about the errors occurring from measured error sequences. From the multitude of analyses in [Wil11][5] only a few are to be quoted here, whereby always the symbol error probability $p_{\rm S} = 10^{-3}$ is the basis.
- In the diagrams, the red curve applies in each case to statistically independent errors $($BSC or $\alpha = 1)$,
- the green curve for a burst error channel with $\alpha = 0.7$. In addition, the following agreement shall apply:
$\text{Definition:}$ An "error burst" $($or "burst" for short$)$ always starts with a symbol error and ends when $k_{\rm Burst}- 1$ error-free symbols follow each other.
- $k_{\rm Burst}$ denotes the "burst end parameter".
- The "burst weight" $G_{\rm Burst}$ corresponds to the number of all symbol errors in the burst.
- For a "single error", $G_{\rm Burst}= 1$ and the "burst length" (determined by the first and last error) is also $L_{\rm Burst}= 1$.
$\text{Example 10:}\ \text{Probability }p_1\text{ of a single error in a sample of length} \ n$
For the BSC channel $(\alpha = 1)$, $p_1 = n \cdot 0.001 \cdot 0.999^{n-1}$ ⇒ red curve.
- Due to the double-logarithmic representation, these numerical values result in a (nearly) linear progression.
- Thus, with the BSC model, single errors occur in a sample of length $n = 100$ with about $9\%$ probability.
In the case of the burst error channel with $\alpha = 0.7$ ⇒ green curve, the corresponding probability is only about $0.7\%$ and the course of the curve is slightly curved here.
In the following calculation, we first assume that the single error in the sample of length $n$ occurs at position $b$:
- Thus, in the case of a single error, $n-b$ error-free symbols must then follow.
- After averaging over the possible error positions $b$, we thus obtain:
- \[p_1 = p_{\rm S} \cdot \sum_{b = 1}^{n} \hspace{0.15cm}V_a (b) \cdot V_a (n+1-b) \hspace{0.05cm}.\]
- Because of its similarity to the signal representation of a "digital filter", the sum can be called "a convolution of $V_a(b)$ with itself".
- For the generating function $V_a(z)$, the convolution becomes a product $[$or the square because of $V_a(b) \star V_a(b)]$ and the following equation is obtained:
- \[V_a(z=1) \cdot V_a(z=1) = \big [ V_a(z=1) \big ]^2 = {\big [ 1 -(1- {p_{\rm S} }^{1/\alpha})\big ]^{-2\alpha} } \hspace{0.05cm}.\]
- Thus, with the "specific error distance distribution" $V_a(z)$, we obtain the following final result:
- \[p_1 = p_{\rm S} \cdot \frac{2\alpha \cdot (2\alpha+1) \cdot \hspace{0.05cm} \text{... } \hspace{0.05cm} \cdot (2\alpha+n-2)} {(n-1)!}\cdot (1- {p_{\rm S} }^{1/\alpha})^{n-1} \hspace{0.05cm}.\]
$\text{Example 11:}\ \text{Mean number of errors } {\rm E}[G_{\rm Burst}] \text{ in a burst with end parameter }k_{\rm Burst}$
Let the mean symbol error probability still be $p_{\rm S} = 10^{-3}$, i.e. (relatively) small.
(A) Red curve for the BSC channel (or $\alpha = 1)$:
- For example, the parameter $k_{\rm Burst}= 10$ means that the burst is finished when nine error-free symbols follow after one error. The probability for an error distance $a \le 9$ is extremely small when $p_{\rm S}$ is small $($here: $10^{-3})$. It further follows that then (almost) every single error is taken as a "burst", and ${\rm E}[G_{\rm Burst}] \approx 1.01$ .
- If the burst end parameter $k_{\rm Burst}$ is larger, the probability ${\rm Pr}(a \le k_{\rm Burst})$ also increases significantly and "bursts" with more than one error occur. For example, if $k_{\rm Burst}= 100$ is chosen, a "burst" contains on average $1.1$ symbol errors.
- This means at the same time, that long error bursts $($according to our definition$)$ can also occur in the BSC model if, for a given $p_{\rm S}$, the burst end parameter is chosen too large or, for a given $k_{\rm Burst}$, the mean error probability $p_{\rm S}$ is too large.
(B) Green curve for the Wilhelm channel with $\alpha = 0.7$:
The procedure given here for the numerical determination of the mean error number ${\rm E}[G_{\rm Burst}]$ of a burst can be applied independently of the $\alpha$–value. One proceeds as follows:
- According to the error distance probabilities ${\rm Pr}(a=k)$ one generates an error sequence $\langle e_1,\ e_2,\ \text{...} ,\ e_i\rangle$, ... with the error distances $a_1$, $a_2$, ... , $a_i$, ...
- If an error distance $a_i \ge k_{\rm Burst}$, this marks the end of a burst. Such an event occurs with probability ${\rm Pr}(a \ge k_{\rm Burst}) = V_a(k_{\rm Burst} )$.
- We count such events "$a_i \ge k_{\rm Burst}$" in the entire block of length $n$. Their number is simultaneously the number of bursts $(N_{\rm Burst})$ in the block.
- At the same time, the relation $N_{\rm Burst} = N_{\rm error} \cdot V_a(k_{\rm Burst} )$ holds, where $N_{\rm error}$ is the number of all errors in the block.
- From this, the average number of errors per burst can be calculated in a simple way:
- \[{\rm E}[G_{\rm Burst}] =\frac {N_{\rm error} }{N_{\rm Burst} } =\frac {1}{V_a(k_{\rm Burst})}\hspace{0.05cm}.\]
The markings in the graph correspond to the following numerical values of the "error distance distribution":
- The green circles $($Wilhelm channel, $\alpha = 0.7)$ result from $V_a(10) = 0.394$ and $V_a(100) = 0.193$.
- The red circles $($BSC channel, $\alpha = 1)$ are the reciprocals of $V_a(10) = 0.991$ and $V_a(100) = 0906$.
Exercises for the chapter
Exercise 5.6: Error Correlation Duration
Exercise 5.6Z: Gilbert-Elliott Model
Exercise 5.7: McCullough and Gilbert-Elliott Parameters
Exercise 5.7Z: McCullough Model once more
References
- ↑ Gilbert, E. N.: Capacity of Burst–Noise Channel. In: Bell Syst. Techn. J. Vol. 39, 1960, pp. 1253–1266.
- ↑ Elliott, E.O.: Estimates of Error Rates for Codes on Burst–Noise Channels. In: Bell Syst. Techn. J., Vol. 42, (1963), pp. 1977 – 1997.
- ↑ Huber, J.: Codierung für gedächtnisbehaftete Kanäle. Dissertation – Universität der Bundeswehr München, 1982.
- ↑ McCullough, R.H.: The Binary Regenerative Channel. In: Bell Syst. Techn. J. (47), 1968.
- ↑ 5.0 5.1 5.2 Wilhelm, C.: A-Model and L-Model, New Channel Models with Formulas for Probabilities of Error Structures. Internet Publication to Channels-Networks, 2011ff.