Difference between revisions of "Aufgaben:Exercise 5.4Z: OVSF Codes"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Spreizfolgen für CDMA }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |ty…“) |
|||
| (23 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Spreading_Sequences_for_CDMA |
}} | }} | ||
| − | [[File:|right|]] | + | [[File:EN_Mod_Z_5_4.png|right|frame|Construction of an OVSF code]] |
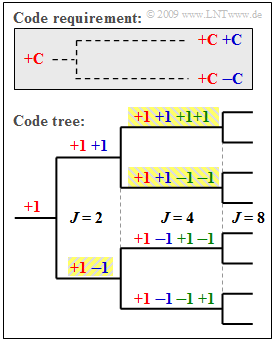
| + | The spreading codes for [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_UMTS|UMTS]] should | ||
| + | * all be orthogonal to each other in order to avoid mutual interference between subscribers, | ||
| + | * additionally allow a flexible realization of different spreading factors $J$. | ||
| − | === | + | One example of this is the so-called [[Modulation_Methods/Spreading_Sequences_for_CDMA#Codes_with_variable_spreading_factor_.28OVSF_codes.29|"Orthogonal Variable Spreading Factor" code]], which provide spreading codes with lengths from $J = 4$ to $J = 512$. |
| + | |||
| + | These can be created using a code tree, as shown in the diagram. In this process, two new codes $(+C \ +C)$ and $(+C \ -C)$ are created from a code $C$ at each branching. | ||
| + | |||
| + | The diagram illustrates the principle given here with the example $J = 4$: | ||
| + | *If the spreading sequences are numbered from $0$ to $J -1$ the spreading sequences are as follows | ||
| + | :$$\langle c_\nu^{(0)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ | ||
| + | :$$\langle c_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$ | ||
| + | *According to this nomenclature, for the spreading factor $J = 8$ there are the spreading sequences $\langle c_\nu^{(0)}\rangle $, ... , $\langle c_\nu^{(7)}\rangle $. | ||
| + | *Note that no predecessor and successor of a code may be used for another participant. | ||
| + | *So, in the example, four spreading codes with spreading factor $J = 4$ could be used or the three codes highlighted in yellow – once with $J = 2$ and twice with $J = 4$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Modulation_Methods/Spreizfolgen_für_CDMA|Spreading Sequences for CDMA]]. | ||
| + | *Reference is made in particular to the section [[Modulation_Methods/Spreading_Sequences_for_CDMA#Codes_with_variable_spreading_factor_.28OVSF_codes.29|Codes with variable spreading factor (OVSF codes)]] in the theory part. | ||
| + | * We would also like to draw your attention to the (German language) interactive SWF module [[Applets:OVSF-Codes_(Applet)|OVSF]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
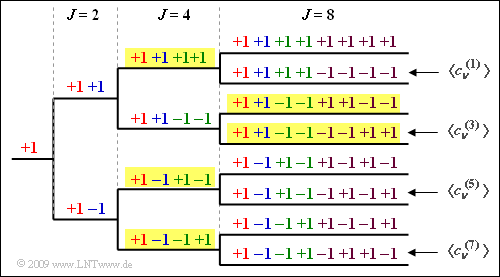
| − | { | + | {Construct the tree diagram for $J = 8$. What are the resulting OVSF codes? |
|type="[]"} | |type="[]"} | ||
| − | - | + | + '''Code word 1:''' $ \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$ |
| − | + | + | - '''Code word 3:''' $ \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1}$ , |
| + | + '''Code word 5:''' $ \langle c_\nu^{(5)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}$, | ||
| + | + '''Code word 7:''' $ \langle c_\nu^{(7)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}$. | ||
| − | { | + | {What is the maximum number of UMTS subscribers $(K_{\rm max})$ that can be served with $J = 8$ ? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $K_{\rm max} \ = \ $ { 8 } |
| − | |||
| + | {How many subscribers $(K)$ can be served if three of these subscribers are to use a spreading code with $J = 4$ ? | ||
| + | |type="{}"} | ||
| + | $K \ = \ $ { 5 } | ||
| + | {Assume a tree structure for $J = 32$. Is the following assignment feasible:<br>Twice $J = 4$, once $J = 8$, twice $J = 16$ and eight times $J = 32$? | ||
| + | |type="()"} | ||
| + | + Yes. | ||
| + | - No. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | [[File:P_ID1892__Mod_Z_5_4a.png|right|frame|OVSF tree structure for $J = 8$]] |
| − | '''2 | + | '''(1)''' The diagram shows the OVSF tree structure for $J = 8$ users. From this it can be seen that <u>solutions 1, 3 and 4</u> apply, but not the second one. |
| − | '''3 | + | |
| − | '''4 | + | |
| − | + | ||
| − | + | '''(2)''' If each user is assigned a spreading code with $J = 8$, $K_{\rm max}\hspace{0.15cm}\underline{ = 8}$ subscribers can be served. | |
| − | + | ||
| + | |||
| + | |||
| + | '''(3)''' When three subscribers are served by $J = 4$ <br> ⇒ only two subscribers can still be served by a spreading sequence with $J = 8$ (see exemplary yellow background in the diagram) ⇒ $K\hspace{0.15cm}\underline{ = 5}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' We denote by | ||
| + | * $K_4 = 2$ the number of spreading sequences with $J = 4$, | ||
| + | * $K_8 = 1$ the number of spreading sequences with $J = 8$, | ||
| + | * $K_{16} = 2$ the number of spreading sequences with $J = 16$, | ||
| + | * $K_{32} = 8$ the number of spreading sequences with $J = 32$. | ||
| + | |||
| + | |||
| + | Then the following condition must be satisfied: | ||
| + | :$$K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} K_4 \cdot8 + K_8 \cdot 4 +K_{16} \cdot 2 +K_{32} \cdot1 \le 32 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Because of $2 · 8 + 1 · 4 + 2 · 2 + 8 = 32$, the desired occupancy is just allowed ⇒ <u>answer YES</u>. | ||
| + | *For example, supplying the spreading factor $J = 4$ twice blocks the upper half of the tree. | ||
| + | *After providing one spreading $J = 8$, three of the eight branches remain to be occupied on the $J = 8$ level, and so on. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^5.3 Spread Sequences for CDMA^]] |
Latest revision as of 17:13, 1 November 2022
The spreading codes for UMTS should
- all be orthogonal to each other in order to avoid mutual interference between subscribers,
- additionally allow a flexible realization of different spreading factors $J$.
One example of this is the so-called "Orthogonal Variable Spreading Factor" code, which provide spreading codes with lengths from $J = 4$ to $J = 512$.
These can be created using a code tree, as shown in the diagram. In this process, two new codes $(+C \ +C)$ and $(+C \ -C)$ are created from a code $C$ at each branching.
The diagram illustrates the principle given here with the example $J = 4$:
- If the spreading sequences are numbered from $0$ to $J -1$ the spreading sequences are as follows
- $$\langle c_\nu^{(0)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$
- $$\langle c_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$
- According to this nomenclature, for the spreading factor $J = 8$ there are the spreading sequences $\langle c_\nu^{(0)}\rangle $, ... , $\langle c_\nu^{(7)}\rangle $.
- Note that no predecessor and successor of a code may be used for another participant.
- So, in the example, four spreading codes with spreading factor $J = 4$ could be used or the three codes highlighted in yellow – once with $J = 2$ and twice with $J = 4$.
Notes:
- The exercise belongs to the chapter Spreading Sequences for CDMA.
- Reference is made in particular to the section Codes with variable spreading factor (OVSF codes) in the theory part.
- We would also like to draw your attention to the (German language) interactive SWF module OVSF.
Questions
Solution
(1) The diagram shows the OVSF tree structure for $J = 8$ users. From this it can be seen that solutions 1, 3 and 4 apply, but not the second one.
(2) If each user is assigned a spreading code with $J = 8$, $K_{\rm max}\hspace{0.15cm}\underline{ = 8}$ subscribers can be served.
(3) When three subscribers are served by $J = 4$
⇒ only two subscribers can still be served by a spreading sequence with $J = 8$ (see exemplary yellow background in the diagram) ⇒ $K\hspace{0.15cm}\underline{ = 5}$.
(4) We denote by
- $K_4 = 2$ the number of spreading sequences with $J = 4$,
- $K_8 = 1$ the number of spreading sequences with $J = 8$,
- $K_{16} = 2$ the number of spreading sequences with $J = 16$,
- $K_{32} = 8$ the number of spreading sequences with $J = 32$.
Then the following condition must be satisfied:
- $$K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_4 \cdot8 + K_8 \cdot 4 +K_{16} \cdot 2 +K_{32} \cdot1 \le 32 \hspace{0.05cm}.$$
- Because of $2 · 8 + 1 · 4 + 2 · 2 + 8 = 32$, the desired occupancy is just allowed ⇒ answer YES.
- For example, supplying the spreading factor $J = 4$ twice blocks the upper half of the tree.
- After providing one spreading $J = 8$, three of the eight branches remain to be occupied on the $J = 8$ level, and so on.