Difference between revisions of "Aufgaben:Exercise 3.2: G-matrix of a Convolutional Encoder"
m (Textersetzung - „* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Algebraic_and_Polynomial_Description}} |
| − | [[File:P_ID2614__KC_A_3_1_neu.png|right|frame| | + | [[File:P_ID2614__KC_A_3_1_neu.png|right|frame|Predefined convolutional encoder]] |
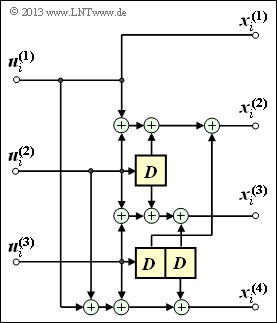
| − | + | We consider as in [[Aufgaben:Exercise_3.1:_Analysis_of_a_Convolutional_Encoder|$\text{Exercise 3.1}$]] the convolutional encoder of rate $3/4$ drawn opposite. This is characterized by the following set of equations: | |
:$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$ | :$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$ | ||
:$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$ | :$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$ | ||
| Line 8: | Line 8: | ||
:$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$ | :$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$ | ||
| − | + | Referring to the sequences $($both starting at $i = 1$ and extending in time to infinity$)$, | |
:$$\underline{\it u} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it u}_1, \underline{\it u}_2, \text{...} \hspace{0.1cm}, \underline{\it u}_i ,\text{...} \hspace{0.1cm} \right )\hspace{0.05cm},$$ | :$$\underline{\it u} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it u}_1, \underline{\it u}_2, \text{...} \hspace{0.1cm}, \underline{\it u}_i ,\text{...} \hspace{0.1cm} \right )\hspace{0.05cm},$$ | ||
:$$\underline{\it x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it x}_1, \underline{\it x}_2, \text{...} \hspace{0.1cm}, \underline{\it x}_i , \text{...} \hspace{0.1cm} \right )$$ | :$$\underline{\it x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it x}_1, \underline{\it x}_2, \text{...} \hspace{0.1cm}, \underline{\it x}_i , \text{...} \hspace{0.1cm} \right )$$ | ||
| − | + | with | |
| + | :$$\underline{u}_i = (u_i^{(1)}, u_i^{(2)}, \ \text{...} \ , u_i^{(k)}),$$ | ||
| + | :$$\underline{x}_i = (x_i^{(1)}, x_i^{(2)}, \ \text{...} \ , x_i^{(n)}),$$ | ||
| + | then the relationship between the information sequence $\underline{u}$ and the code sequence $\underline{x}$ can be expressed by the generator matrix $\mathbf{G}$ in the following form: | ||
:$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$ | :$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$ | ||
| − | + | For the generator matrix of a convolutional encoder with memory $m$ is to be set: | |
:$${ \boldsymbol{\rm G}}=\begin{pmatrix} | :$${ \boldsymbol{\rm G}}=\begin{pmatrix} | ||
{ \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ | { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ | ||
| Line 23: | Line 26: | ||
\end{pmatrix}\hspace{0.05cm}.$$ | \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | + | *Hereby denote $\mathbf{G}_0, \ \mathbf{G}_1, \ \mathbf{G}_2, \ \text{...}$ partial matrices each having $k$ rows and $n$ columns and binary matrix elements $(0$ or $1)$. | |
| + | |||
| + | *If the matrix element $\mathbf{G}_l(\kappa, j) = 1$, it means that the code bit $x_i^{(j)}$ is affected by the information bit $u_{i-l}^{(\kappa)}$ . | ||
| + | |||
| + | *Otherwise, this matrix element is $\mathbf{G}_l(\kappa, j) =0$. | ||
| + | |||
| − | + | ⇒ The goal of this exercise is to compute the code sequence $\underline{x}$ belonging to the information sequence | |
:$$\underline{u} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 | :$$\underline{u} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 | ||
\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm} | \hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm} | ||
,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})$$ | ,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})$$ | ||
| − | + | according to the above specifications. The result should match the result of [[Aufgaben:Exercise_3.1:_Analysis_of_a_Convolutional_Encoder| $\text{Exercise 3.1}$]] which was obtained in a different way. | |
| + | |||
| Line 36: | Line 45: | ||
| − | + | ||
| − | + | ||
| + | Hints: This exercise belongs to the chapter [[Channel_Coding/Algebraic_and_Polynomial_Description| "Algebraic and Polynomial Description"]]. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {From how many partial matrices $\mathbf{G}_l$ is the matrix $\mathbf{G}$ composed? |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{number of partial matrices} \ = \ ${ 3 3% } |
| − | { | + | {Which statements are true for the partial matrix $\mathbf{G}_0$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + In total, $\mathbf{G}_0$ contains eight ones. |
| − | + | + | + The first row of $\mathbf{G}_0$ is $1 \ 1 \ 0 \ 1$. |
| − | - | + | - The first row of $\mathbf{G}_0$ is $1 \ 0 \ 0$. |
| − | { | + | {Which statements are true for the partial matrix $\mathbf{G}_1$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The first row is $0 \ 0 \ 0 \ 0$. |
| − | + | + | + The second row is $0 \ 1 \ 1 \ 0$. |
| − | + | + | + The third row is $0 \ 1 \ 0 \ 0$. |
| − | { | + | {Determine the first nine rows and twelve columns of the generator matrix $\mathbf{G}$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - There is at least one row with all zeros. |
| − | - | + | - There is at least one row with all ones. |
| − | + In | + | + In each of the columns $1,\ 5,\ 9$ there is only one single one. |
| − | { | + | {What code sequence $\underline {x}$ results for $\underline {u} = (0, 1, 1, 1, 1, 0, 1, 0, 1)$? |
|type="()"} | |type="()"} | ||
| − | - | + | - It holds: $\underline{x} = (1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, \ \text{...})$. |
| − | + | + | + It holds: $\underline{x} = (0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, \ \text{...})$. |
| − | - | + | - It holds: $\underline{x} = (0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, \ \text{...})$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The memory of the considered convolutional encoder is $m = 2$. |
| + | *Thus, the generator matrix $\mathbf{G}$ is composed of the $m + 1 \ \underline {= 3}$ submatrices $\mathbf{G}_0, \mathbf{G}_1$ and $\mathbf{G}_2$. | ||
| − | '''(2)''' | + | |
| − | * | + | '''(2)''' Correct are <u>statement 1 and 2</u>: |
| + | *From the given equations | ||
:$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$ | :$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$ | ||
:$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$ | :$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$ | ||
:$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$ | :$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$ | ||
| − | :$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}$$ | + | :$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)},$$ |
| + | |||
| + | it can be seen that in the whole equation set an input value $u_i^{(j)}$ with $j ∈ \{1,\ 2,\ 3\}$ occurs exactly eight times ⇒ Statement 1 is true. | ||
| + | |||
| + | *The input value $u_i^{(1)}$ influences the outputs $x_i^{(1)}$, $x_i^{(2)}$ and $x_i^{(4)}$. Thus, the first row of $\mathbf{G}_0 \text{ is} \, 1 \ 1 \ 0 \ 1$ ⇒ Statement 2 is true too. | ||
| + | |||
| + | *In contrast, statement 3 is false: It is not the first row of $\mathbf{G}_0$ that is $1 \ 0 \ 0$, but the first column. | ||
| + | |||
| + | *This says that $x_i^{(1)}$ depends only on $u_i^{(1)}$, but not on $u_i^{(2)}$ or on $u_i^{(3)}$. It is a systematic code. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' <u>All statements are accurate</u>: | ||
| + | *In the equation set, an input value $u_{i–1}^{(j)}$ with $j ∈ \{1,\ 2,\ 3\}$ occurs three times. Thus, $\mathbf{G}_1$ contains a total of three ones. | ||
| − | + | *The input value $u_{i-1}^{(2)}$ influences the outputs $x_i^{(2)}$ and $x_i^{(3)}$, while $u_{i-1}^{(3)}$ is used only for the calculation of $x_i^{(2)}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
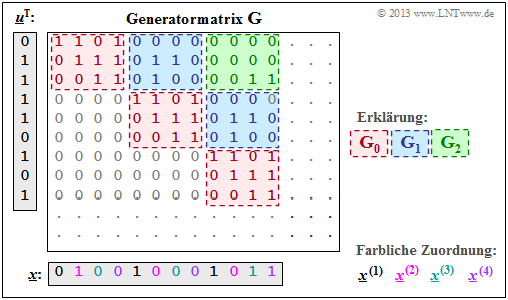
| + | [[File:P_ID2615__KC_A_3_2d_v1.png|right|frame|Generator matrix of a convolutional code with $k = 4, \ n = 4, \ m = 2$.]] | ||
| + | '''(4)''' Only <u>statement 3</u> is correct: | ||
| + | *The following graph shows the upper left beginning $($rows 1 to 9 and columns 1 to 12$)$ of the generator matrix $\mathbf{G}$. | ||
| + | |||
| + | *From this it can be seen that the first two statements are false. | ||
| + | |||
| + | *This result holds for any systematic code with parameters $k = 3$ and $n = 4$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' | + | '''(5)''' Correct is <u>statement 2</u>: |
| − | * | + | *Generally, $\underline{x} = \underline{u} \cdot \mathbf{G}$, where $\underline{u}$ and $\underline{x}$ are sequences, that is, they continue to infinity. |
| − | * | + | |
| − | * | + | *Accordingly, the generator matrix $\mathbf{G}$ is not limited downward or to the right. |
| − | * | + | |
| + | *If the information sequence $\underline{u}$ is limited $($here to $9$ bits$)$, the code sequence $\underline{x}$ is also limited. | ||
| + | |||
| + | *If one is only interested in the first bits, it is sufficient to look only at the upper left section of the generator matrix as in the sample solution to subtask '''(4)'''. | ||
| + | |||
| + | *Using this graph, the result of the matrix equation $\underline{x} = \underline{u} \cdot \mathbf{G}$ can be read off. | ||
| + | |||
| + | *Correct is $\underline{x} = (0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, \ ...)$ and thus answer 2. | ||
| + | |||
| + | We obtained the same result in the; subtask '''(4)'''  of [[Aufgaben:Exercise_3.1:_Analysis_of_a_Convolutional_Encoder|$\text{Exercise 3.1}$]]. | ||
| − | + | *Shown here are only $9$ information bits and $9 \cdot n/k = 12$ code bits. | |
| − | * | + | *Due to the partial matrices $\mathbf{G}_1$ and $\mathbf{G}_2$, however, (partial) ones would still result here for the code bits 13 to 20. |
| − | * | + | *The code sequence $\underline{x}$ is composed of the four subsequences $\underline{x}^{(1)}, \ \text{...} \ , \ \underline{x}^{(4)}$, which can be read in the graphic due to different coloring. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^3.2 Polynomial Description^]] |
Latest revision as of 15:31, 9 November 2022
We consider as in $\text{Exercise 3.1}$ the convolutional encoder of rate $3/4$ drawn opposite. This is characterized by the following set of equations:
- $$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$
- $$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$
- $$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$
- $$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$
Referring to the sequences $($both starting at $i = 1$ and extending in time to infinity$)$,
- $$\underline{\it u} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it u}_1, \underline{\it u}_2, \text{...} \hspace{0.1cm}, \underline{\it u}_i ,\text{...} \hspace{0.1cm} \right )\hspace{0.05cm},$$
- $$\underline{\it x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it x}_1, \underline{\it x}_2, \text{...} \hspace{0.1cm}, \underline{\it x}_i , \text{...} \hspace{0.1cm} \right )$$
with
- $$\underline{u}_i = (u_i^{(1)}, u_i^{(2)}, \ \text{...} \ , u_i^{(k)}),$$
- $$\underline{x}_i = (x_i^{(1)}, x_i^{(2)}, \ \text{...} \ , x_i^{(n)}),$$
then the relationship between the information sequence $\underline{u}$ and the code sequence $\underline{x}$ can be expressed by the generator matrix $\mathbf{G}$ in the following form:
- $$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$
For the generator matrix of a convolutional encoder with memory $m$ is to be set:
- $${ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \ddots & \ddots & & & \ddots \end{pmatrix}\hspace{0.05cm}.$$
- Hereby denote $\mathbf{G}_0, \ \mathbf{G}_1, \ \mathbf{G}_2, \ \text{...}$ partial matrices each having $k$ rows and $n$ columns and binary matrix elements $(0$ or $1)$.
- If the matrix element $\mathbf{G}_l(\kappa, j) = 1$, it means that the code bit $x_i^{(j)}$ is affected by the information bit $u_{i-l}^{(\kappa)}$ .
- Otherwise, this matrix element is $\mathbf{G}_l(\kappa, j) =0$.
⇒ The goal of this exercise is to compute the code sequence $\underline{x}$ belonging to the information sequence
- $$\underline{u} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm} ,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})$$
according to the above specifications. The result should match the result of $\text{Exercise 3.1}$ which was obtained in a different way.
Hints: This exercise belongs to the chapter "Algebraic and Polynomial Description".
Questions
Solution
- Thus, the generator matrix $\mathbf{G}$ is composed of the $m + 1 \ \underline {= 3}$ submatrices $\mathbf{G}_0, \mathbf{G}_1$ and $\mathbf{G}_2$.
(2) Correct are statement 1 and 2:
- From the given equations
- $$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$
- $$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$
- $$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$
- $$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)},$$
it can be seen that in the whole equation set an input value $u_i^{(j)}$ with $j ∈ \{1,\ 2,\ 3\}$ occurs exactly eight times ⇒ Statement 1 is true.
- The input value $u_i^{(1)}$ influences the outputs $x_i^{(1)}$, $x_i^{(2)}$ and $x_i^{(4)}$. Thus, the first row of $\mathbf{G}_0 \text{ is} \, 1 \ 1 \ 0 \ 1$ ⇒ Statement 2 is true too.
- In contrast, statement 3 is false: It is not the first row of $\mathbf{G}_0$ that is $1 \ 0 \ 0$, but the first column.
- This says that $x_i^{(1)}$ depends only on $u_i^{(1)}$, but not on $u_i^{(2)}$ or on $u_i^{(3)}$. It is a systematic code.
(3) All statements are accurate:
- In the equation set, an input value $u_{i–1}^{(j)}$ with $j ∈ \{1,\ 2,\ 3\}$ occurs three times. Thus, $\mathbf{G}_1$ contains a total of three ones.
- The input value $u_{i-1}^{(2)}$ influences the outputs $x_i^{(2)}$ and $x_i^{(3)}$, while $u_{i-1}^{(3)}$ is used only for the calculation of $x_i^{(2)}$.
(4) Only statement 3 is correct:
- The following graph shows the upper left beginning $($rows 1 to 9 and columns 1 to 12$)$ of the generator matrix $\mathbf{G}$.
- From this it can be seen that the first two statements are false.
- This result holds for any systematic code with parameters $k = 3$ and $n = 4$.
(5) Correct is statement 2:
- Generally, $\underline{x} = \underline{u} \cdot \mathbf{G}$, where $\underline{u}$ and $\underline{x}$ are sequences, that is, they continue to infinity.
- Accordingly, the generator matrix $\mathbf{G}$ is not limited downward or to the right.
- If the information sequence $\underline{u}$ is limited $($here to $9$ bits$)$, the code sequence $\underline{x}$ is also limited.
- If one is only interested in the first bits, it is sufficient to look only at the upper left section of the generator matrix as in the sample solution to subtask (4).
- Using this graph, the result of the matrix equation $\underline{x} = \underline{u} \cdot \mathbf{G}$ can be read off.
- Correct is $\underline{x} = (0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, \ ...)$ and thus answer 2.
We obtained the same result in the; subtask (4)  of $\text{Exercise 3.1}$.
- Shown here are only $9$ information bits and $9 \cdot n/k = 12$ code bits.
- Due to the partial matrices $\mathbf{G}_1$ and $\mathbf{G}_2$, however, (partial) ones would still result here for the code bits 13 to 20.
- The code sequence $\underline{x}$ is composed of the four subsequences $\underline{x}^{(1)}, \ \text{...} \ , \ \underline{x}^{(4)}$, which can be read in the graphic due to different coloring.