Channel Coding/Examples of Binary Block Codes

1. Channel Coding
2. Binary Block Codes for Channel Coding
3. Examples of Binary Block Codes

• Previous page
• Next page

• Previous page
• Next page

Single Parity-check Codes

The  »Single parity-check code«  $\rm (SPC)$  adds to the information block  $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$  a parity bit  $p$:

Various single parity-check codes  $(n = k + 1)$

$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$

$$\Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.$$

The graphic shows three coding examples:

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \hspace{0.15cm} (k = 2)$,

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \hspace{0.15cm} (k = 3)$,

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \hspace{0.15cm} (k = 4)$.

This very simple code can be characterized as follows:

• From  $n = k + 1$  follows for the  »code rate«  $R = k/n = (n-1)/n$  and for the  »redundancy«  $1-R = 1/n$.  For  $k = 2$,  for example,  the code rate is  $2/3$  and the relative redundancy is  $33.3\%$.

• The parity bit is obtained by  »modulo–2«  addition.  This is the addition in the  $\text{Galois field}$  to the base  $2$   ⇒   $\rm GF(2)$,  so that  $1 \oplus 1 = 0$  results:

\[p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.\]

• Thus every valid code word  $\underline{x}$  contains an even number of ones.  Expressed as  $\oplus$  or in simplified notation according to the second equation,  this condition reads:

\[ x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm or:}\hspace{0.5cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}. \]

• For  $k = 2$   ⇒   $n = 3$  the following four code words result,  where the parity bit  $p$  is marked by a small arrow in each case:

\[\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.\]

• This code  $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$  is  »linear« since the sum of any two code words again gives a valid code word,  for example:

$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$

• For any  $k$   ⇒   $n = k+1$  each code word differs from all others at an even number of positions.  Thus,  the minimum distance of the code is 

$$d_{\rm min} = 2.$$

$\text{Definition:}$  Each  $\text{single parity-check code (SPC)}$  can be formally described as follows:

\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm with \hspace{0.15cm}even\hspace{0.15cm} number\hspace{0.15cm} of\hspace{0.15cm} ones\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.\]

• With the general code name  $(n, \ k, \ d_{\rm min})$  any single parity–check code can also be named  $\text{SPC }(n, \ n-1, \ 2)$ .

• The top graph thus shows the  $\text{SPC (3, 2, 2)}$,  the  $\text{SPC (4, 3, 2)}$,  and the  $\text{SPC (5, 4, 2)}$.

The digital channel may change the code word  $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$  to the received word  $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. With the error vector  $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$  holds:

$$\underline{y}= \underline{x} \oplus \underline{e}.$$

For  $\text{decoding the single parity-check code}$  one forms the so-called  »syndrome«:

\[s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.\]

The result  $s=1$  then indicates  (at least)  one bit error within the code word,  while  $s=0$  should be interpreted as follows:

• The transmission was error-free, or:
  
• the number of bit errors is even.
  
  

$\text{Example 1:}$  We consider the  $\text{SPC (4, 3, 2)}$  and assume that the all-zero word was sent.  The table shows all possibilities that  $f$  bits are corrupted KORREKTUR: falsified and gives the respective syndrome  $s \in \{0, 1\}$. 

Possible received values at the  $\text{SPC (4, 3, 2)}$

For the  $\text{BSC model}$  with the crossover probability  $\varepsilon = 1\%$  the following probabilities then result:

• The information word is correctly decoded  (blue background):

\[{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.\]

• The decoder detects that transmission errors have occurred  (green background):

$${\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm odd} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f}$$

$$\Rightarrow \hspace{0.3cm} {\rm Pr}(s=1) \hspace{-0.1cm} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.$$

• The information word is decoded incorrectly  (red background):

\[{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.\]

We refer here to the HTML5/JavaScript applet  $\text{Binomial and Poisson Distribution}$.  The results obtained here are also discussed in  $\text{Exercise 1.5}$.

$\text{Example 2:}$  Error correction of the single parity–check code is not possible for the BSC model unlike the  $\text{BEC model}$  ("Binary Erasure Channel").

Bit errors are excluded with this one.  If only one bit is erased  $($"erasure",  $\rm E)$,  then due to the fact  "the number of ones in the code word is even",  error correction is also possible,  for example for the  $\text{SPC (5, 4, 2)}$:

\[\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},\] \[\underline{y}=(0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},\] \[\underline{y} = (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.\]

$\text{Example 3:}$  Also with the  $\text{AWGN model}$  error correction is possible when applying  "soft decision".  For the following we assume bipolar signaling:

To clarify  "soft decision"  at AWGN

• $x=0$   ⇒   $\tilde{x}= +1$,  as well as
• $x=1$   ⇒   $\tilde{x}= -1$.
  

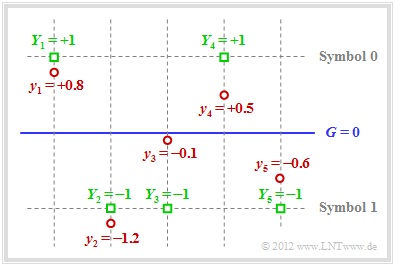
The graphic illustrates the facts presented here:

• For example,  the received vector is  (red dots):

\[\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.\]

• With a hard decision  $($threshold  $G = 0$,  only the signs are evaluated$)$  one would arrive at the following binary result  $($green squares  $Y_i = y_i/ \vert y_i \vert)$:

\[\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.\]

• In symbol notation,  this gives  $(0, 1, 1, 0, 1)$,  which is not a valid code word of  $\text{SPC (5, 4, 2)}$  ⇒   syndrome  $s = 1$.  So one,  three or five bits must have been corrupted KORREKTUR: falsified.
  

• The probability for three or five bit errors,  however,  is orders of magnitude smaller than that for a single error.  The assumption of  "one bit error"  is therefore not unreasonable.
  

• Since the received value  $y_3$  is very close to the threshold  $G = 0$  it is assumed that exactly this bit has been corrupted KORREKTUR: falsified.  Thus,  with "soft decision",  the decision is for  $\underline{z} = (0, 1, 0, 0, 1)$   ⇒   $\underline{v} = (0, 1, 0, 0)$.  The block error probability  ${\rm Pr}(\underline{v} \ne \underline{u})$  is thus lowest.

Repetition Codes

$\text{Definition:}$  A  $\text{repetition code}$  ($\rm RC)$  is a linear binary  $(n, \, k)$  block code of the form

\[\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.25cm}{\rm for \hspace{0.25cm}all\hspace{0.35cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.\]

• The code parameter  $n$  denotes the code length.  Independent of  $n$  always holds  $k = 1$.

• Accordingly,  there exist only the two code words  $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$  and  $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$, which differ in  $n$  binary places.

• From this follows for the minimum distance  $d_{\rm min} = n$.

The graphic shows repetition codes for  $n=3$,  $n=4$  and  $n=5$.  Such a repetition code has the following properties:

Various repetition codes

• This  $(n, \, 1, \, n)$  block code has the very small code rate  $R = 1/n$.

• So,  such a code is only suitable for transferring or storing small files.

• On the other hand,  the repetition code is very robust.

• In particular,  in the  $\text{BEC channel}$  ("Binary Erasure Channel"),  a single correctly transmitted bit at any position  (all other bits may be erased)  is sufficient to correctly decode the information word.
  

$\text{Example 4: Decoding and error probabilities of the repetition code at the BSC channel}$

The  $\text{BSC channel}$  with  $\varepsilon = 10\%$  applies.  The decoding is based on the majority principle.

• For odd  $n$   ⇒   $e=n-1$ bit errors can be detected and  $t=(n-1)/2$  bit errors can be corrected.

• This gives for the probability of correct decoding of the information bit  $u$:

\[{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.\]

• The following numerical values are valid for  $n = 5$. That means:   There are  $t = 2$  bit errors correctable:

\[{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%\]

\[\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.\]

• On the other hand,  with even  $n$  only  $t=n/2-1$  errors can be corrected.  If  $n$  is increased from  $5$  to  $6$,  then only two bit errors within a code word can be corrected.  A third bit error cannot be corrected,  but at least it can be recognized:

\[{\rm Pr}({\rm not\hspace{0.15cm} correctable\hspace{0.15cm} error}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}. \]

• An  (undetected)  decoding error  $(v \ne u)$  results only when four or more bits have been corrupted KORREKTUR: falsified within the six bit word.  As an approximation,  assuming that five or six bit errors are much less likely than four:

\[{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.\]

• It is interesting to note that for  $\text{RC(6, 1, 6)}$  the probability  ${\rm Pr}(v = u)$  for a possible and correct decoding with  $98.42\%$  is smaller than for  $\text{RC (5, 1, 5)}$.
  For the latter:   ${\rm Pr}(v = u) \approx 99.15\%.$

$\text{Example 5: Performance of the repetition code at the AWGN channel}$

We now consider the  $\text{AWGN channel}$.  For uncoded transmission  $($or the repetition code with  $n=1)$  the received value is  $y = \tilde{x}+\eta$ , where  $\tilde{x} \in \{+1, -1\}$  denotes the information bit in bipolar signaling and  $\eta$  denotes the noise term.  To avoid confusion with the code parameter  $n$  we have renamed the noise:   $n → \eta$.

For the error probability, with the  $\text{complementary Gaussian error integral}$  ${\rm Q}(x)$

\[{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},\]

where the following physical quantities are to be used:

• the signal-to-noise ratio  $\rm (SNR)$  $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,
  

• the energy  $E_{\rm S}$  per code symbol   ⇒   "symbol energy",
  

• the normalized standard deviation  $\sigma$  of the noise,  valid for the bipolar information bit  $\tilde{x} \in \{+1, -1\}$,  and
  

• the constant  (one-sided)  noise power density  $N_0$  of the AWGN noise.
  
  

Error probability of the repetition code at the AWGN channel

In contrast,  for a  $(n,\ 1,\ n)$  repetition code,  the input value of the maximum likelihood decoder  $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$  with the following properties:

\[\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fold \hspace{0.15cm}amplitude}\]

\[\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fold \hspace{0.15cm}power}\hspace{0.05cm},\]

\[\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fold \hspace{0.15cm}variance:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},\]

\[\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.\]

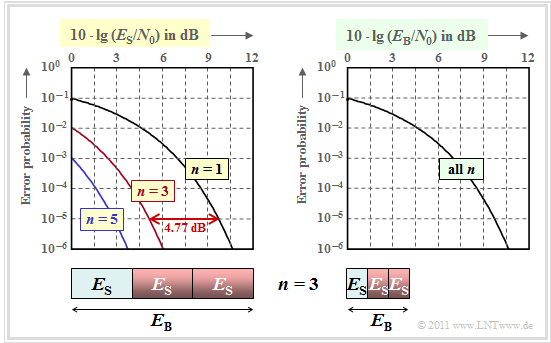
The error probability in double logarithmic representation is shown in the left graph.

1. As abscissa is  $10 \cdot \lg \, (E_{\rm S}/N_0)$  plotted.
2. The energy per bit  $(E_{\rm B})$  is  $n$  times larger than the symbol energy  $E_{\rm S}$,  as illustrated in the graph for  $n=3$ .

This set of curves can be interpreted as follows:

• If one plots the error probability over the abscissa  $10 \cdot \lg \, (E_{\rm S}/N_0)$  then  $n$–times repetition over uncoded transmission  $(n=1)$  results in a significant improvement.
  

• The curve for the repetition factor  $n$  is obtained by left shifting by  $10 \cdot \lg \, n$  $($in  $\rm dB)$  with respect to the comparison curve. 
  The gain is  $4.77 \ {\rm dB} \ (n = 3)$  or  $\approx 5 \ {\rm dB} \ (n = 5)$.
  

• However,  a comparison at constant  $E_{\rm S}$  is not fair,  since with the repetition code  $\text{RC (5, 1, 5)}$  one spends a factor  $n$  larger energy for the transmission of an information bit than with uncoded transmission:   $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$

From the graph on the right,  we can see that all the curves lie exactly on top of each other when plotted on the abscissa  $10 \cdot \lg \, (E_{\rm B}/N_0)$.

$\text{Conclusion regarding repetition codes on the AWGN channel:}$

• The error probability is independent of the repetition factor  $n$  for a fair comparison:     ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) \hspace{0.05cm}.$

• For the AWGN channel,  no  $\text{coding gain}$  can be achieved by a repetition code.

Hamming Codes

In 1962  $\text{Richard Wesley Hamming}$  specified a class of binary block codes that differ in the number  $m = 2, 3, \text{...} $  of added  "parity bits".  For this code class:

• The code length always results in  $n = 2^m -1$.  Consequently,  only the lengths  $n = 3$,  $n = 7$,  $n = 15$,  $n = 31$,  $n = 63$,  $n = 127$,  $n = 255$, etc. are possible.
  

• An information word consists of  $k = n-m$  bits.  The code rate is therefore equal to

\[R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} \text{...} \hspace{0.05cm} \}\hspace{0.05cm}.\]

• All Hamming codes have the minimum distance  $d_{\rm min} = 3$.  With larger code length  $n$  one reaches  $d_{\rm min} = 3$  already with less redundancy, i.e. with larger code rate  $R$.
  

• It further follows from the statement  $d_{\rm min} = 3$  that here only  $e = d_{\rm min} -1 =2$  errors can be detected and only one error can  $t = (d_{\rm min} -1)/2 = 1$  correct errors.
  

• The Hamming code  $\text{HC (3, 1, 3)}$  is identical to the repetition code  $\text{RP (3, 1, 3)}$  and is:

\[\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.25cm}, (1, 1, 1) \big \}\hspace{0.05cm}. \]

• In systematic coding,  the first  $k$  digits of each Hamming code word  $\underline{x}$  are identical to the information word  $\underline{u}$.  This is then followed by  $m = n-k$  parity bits:

\[\underline{x} = ( x_1,\ x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm},\ x_n) = ( u_1,\ u_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ u_k,\ p_1,\ p_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ p_{n-k}) \hspace{0.05cm}.\]

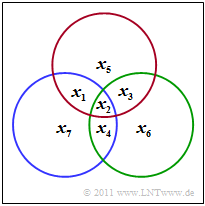
$\text{Example 6: Parity equations of the (7, 4, 3) Hamming code}$

Chart of the  $\text{HC (7, 4, 3)}$

The  $\text{(7, 4, 3)}$  Hamming code is illustrated by the diagram shown.  From it one can derive the three conditions:

\[x_1 \oplus x_2 \oplus x_3 \oplus x_5 = 0 \hspace{0.05cm},\]

\[x_2 \oplus x_3 \oplus x_4 \oplus x_6 = 0 \hspace{0.05cm},\]

\[x_1 \oplus x_2 \oplus x_4 \oplus x_7 = 0 \hspace{0.05cm}. \]

• In the diagram,  the red circle indicates the first test equation,  the green the second and the blue the last.

• In each circle,  the number of ones must be even.

Assignment  $\underline{u} → \underline{x}$  of the systematic $\text{(7, 4, 3)}$ Hamming code

In systematic coding of the  $\text{(7, 4, 3)}$ Hamming code

\[x_1 = u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm} x_5 = p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3 \]

are the equations of determination of the three test bits, as shown in the diagram:

\[p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},\]

\[p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},\]

\[p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.\]

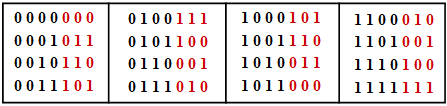
The table shows the  $2^k = 16$  allowed code words of the systematic  $\text{HC (7, 4, 3)}$:

$$\underline{x} = ( x_1,\ x_2,\ x_3,\ x_4,\ x_5,\ x_6,\ x_7) = ( u_1,\ u_2,\ u_3,\ u_4,\ p_1,\ p_2,\ p_3).$$

• The information word  $\underline{u} =( u_1,\ u_2,\ u_3,\ u_4)$  is shown in black and the check bits  $p_1$,  $p_2$  and  $p_3$  in red.

• It can be seen from this table that each two of the  $16$  possible code words differ in at least  $d_{\rm min} = 3$  binary values.

Later the  $\text{Decoding of linear block codes}$  will be covered in more detail.  The following example is intended to explain the decoding of the Hamming code rather intuitively.

$\text{Example 7: Parity equations of the HC (7, 4, 3)}$

We further assume the systematic  $\text{(7, 4, 3)}$ Hamming code and consider the received word  $\underline{y} = ( y_1,\ y_2,\ y_3,\ y_4,\ y_5,\ y_6,\ y_7)$.

For decoding,  we form the three parity equations

\[ y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} \]

\[y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)} \]

\[y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}\]

In the following  $\underline{v}$  denotes the decoding result; this should always match  $\underline{u} = (1,\ 0,\ 1,\ 0)$. 

Provided that at most one bit is corrupted KORREKTUR: falsified in each code word,  the following statements are then valid:

• The received word  $\underline{y} = (1,\ 0,\ 1,\ 0,\ 0,\ 1,\ 1)$  satisfies all three parity equations. This means that not a single transmission error has occurred   ⇒   $\underline{y} = \underline{x}$   ⇒   $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.
  

• If two of the three parity equations are satisfied,  such as for the received word  $\underline{y} =(1,\ 0,\ 1,\ 0,\ 0,\ 1,\ 0)$,  then one parity bit has been corrupted KORREKTUR: falsified and the following also applies here  $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.
  

• With  $\underline{y} = (1,\ 0,\ 1,\ 1,\ 0,\ 1,\ 1)$  only the equation  $\rm (I)$  is satisfied and the other two are not.  Thus,  the corruption of the fourth binary symbol can be corrected,  and it is also valid here  $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.
  

• A transmission error of the second bit   ⇒   $\underline{y} = (1,\ 1,\ 1,\ 0,\ 0,\ 1,\ 1)$  leads to the fact that all three parity equations are not fulfilled.  This error can also be clearly corrected since only  $u_2$  occurs in all equations.

Exercises for the chapter

Exercise 1.5: SPC (5, 4) and BEC Model

Exercise 1.5Z: SPC (5, 4) vs. RC (5, 1)

Exercise 1.6: (7, 4) Hamming Code