Difference between revisions of "Aufgaben:Exercise 3.8: Rate Compatible Punctured Convolutional Codes"
| (50 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Code_Description_with_State_and_Trellis_Diagram}} |
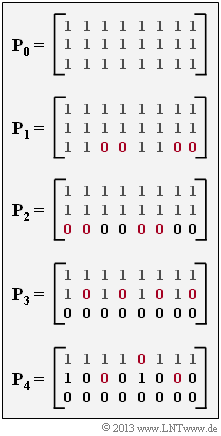
| − | [[File:P_ID2708__KC_A_3_8.png|right|frame| | + | [[File:P_ID2708__KC_A_3_8.png|right|frame|RCPC puncturing matrices]] |
| − | + | An important application for [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Punctured_convolutional_codes|$\text{punctured convolutional codes}$]] are the "Rate Compatible Punctured Convolutional Codes" $($for short: '''RCPC–Codes'''$)$ proposed by Joachim Hagenauer in '''[Hag88]'''. | |
| − | + | Starting from a mother code $\mathcal{C}_0$ with rate $R_0 = 1/n$, other codes $\mathcal{C}_l$ with higher code rate $(R_l > R_0)$ are determined by different puncturing matrices $\mathbf{P}_l$. | |
| − | + | The puncturing matrices $\mathbf{P}_0, \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \mathbf{P}_4$ to be analyzed are shown on the right. | |
| + | *If for the matrix $\mathbf{P}_l$ the matrix element $P_{ij} = 1$, the corresponding code bit is transmitted, while $P_{ij} = 0$ indicates puncturing. | ||
| + | |||
| + | *In the questionnaire, we also use the shorter notation $P_{ij}^{(l)}$ for the element $P_{ij}$ of the matrix $\mathbf{P}_l$. | ||
| − | + | *In the graph: All the zeros in the matrix $\mathbf{P}_l$ that were still ones in the matrix $\mathbf{P}_{l–1}$ are marked in red. This measure increases the code rate $R_{l}$ compared to $R_{l-1}$. | |
| − | |||
| − | |||
| − | |||
| + | The RCPC–codes are well suited for the realization of | ||
| + | * "unequal error protection" for hybrid ARQ procedures, | ||
| − | + | * systems with "incremental redundancy". This means that after conventional convolutional coding, bits corresponding to the puncturing matrix $\mathbf{P}_l$ are omitted from the code word $\underline{x}^{(0)}$ and the shortened code word $\underline{x}^{(l)}$ is transmitted: | |
| + | :*If the punctured code word cannot be correctly decoded in the receiver, the receiver requests further redundancy from the transmitter in the form of the previously punctured bits. | ||
| + | :*This prevents the transmission of redundancy that is not required and adapts the throughput to the channel conditions. | ||
| + | [[File:P_ID2709__hagenauer_kleiner.jpg|left|frame|Joachim Hagenauer]] | ||
| Line 25: | Line 30: | ||
| − | |||
| − | |||
| − | |||
| + | Hints: | ||
| + | * This exercise refers to the section [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Punctured_convolutional_codes|"Punctured convolutional codes"]] in the chapter "Code description with state and trellis diagram". | ||
| + | |||
| + | *The reference '''[Hag88]''' refers to the paper "Hagenauer, J.: Rate Compatible Punctured Convolutional Codes (RCPC codes) and their Applications. In: IEEE Transactions on Communications, vol COM-36, pp 389 - 400, 1988." | ||
| − | === | + | *Professor [https://www.ce.cit.tum.de/en/lnt/people/professors/hagenauer/ $\text{Joachim Hagenauer}$] was head of the Institute of Communications Engineering $\rm(LNT)$ at the Technical University of Munich from 1993 to 2006. The initiators of the learning tutorial $($Günter Söder and Klaus Eichin$)$ thank their long-time boss for supporting and promoting our $\rm LNTwww$ project during the first six years. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements do the given puncturing matrices provide? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The rate of the RCPC mother code is $R_0 = 1/3$. |
| − | - | + | + The puncturing period is $p = 8$. |
| + | - The memory of the RCPC code class is $M = 4$. | ||
| − | { | + | {Which code rates do the codes $\mathcal{C}_1$, ... , $\mathcal{C}_4$ have? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm matrix \ P_1} \ \Rightarrow \ {\rm code \ \mathcal{C}_1} \text{:} \hspace{0.4cm} R_1 \ = \ ${ 0.4 3% } |
| + | ${\rm matrix \ P_2} \ \Rightarrow ß {\rm code \ \mathcal{C}_2} \text{:} \hspace{0.4cm}R_2 \ = \ ${ 0.5 3% } | ||
| + | ${\rm matrix \ P_3} \ \Rightarrow \ {\rm code \ \mathcal{C}_3} \text{:} \hspace{0.4cm} R_3 \ = \ ${ 0.667 3% } | ||
| + | ${\rm matrix \ P_4} \ \Rightarrow \ {\rm code \ \mathcal{C}_4} \text{:} \hspace{0.4cm} R_4 \ = \ ${ 0.889 3% } | ||
| + | |||
| + | {Which statements are valid for the matrix elements $P_{ij}^{(l)}$? | ||
| + | |type="[]"} | ||
| + | + From $P_{ij}^{(l)} = 1$ follows $P_{ij}^{(\lambda)} = 1$ for all $\lambda < l$. | ||
| + | - From $P_{ij}^{(l)} = 1$ follows $P_{ij}^{(\lambda)} = 1$ for all $\lambda > l$. | ||
| + | - From $P_{ij}^{(l)} = 0$ follows $P_{ij}^{(\lambda)} = 0$ for all $\lambda < l$. | ||
| + | + From $P_{ij}^{(l)} = 0$ follows $P_{ij}^{(\lambda)} = 0$ for all $\lambda > l$. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 1 and 2</u>: |
| − | + | *The number of rows of the puncturing matrices gives the parameter $n$ of the $(n, \ k = 1)$ RCPC mother code. | |
| − | + | ||
| − | '''( | + | *From this, its rate is $R_0 = 1/3$. The column number is equal to the puncturing period $p$. For the class of codes under consideration: $p = 8$. |
| − | + | ||
| − | {{ | + | * In contrast, the puncturing matrices do not provide any information about the memory of the code. |
| + | |||
| + | |||
| + | '''(2)''' For the rate of code $\mathcal{C}_l = p/N_l$, where $N_l$ denotes the number of all ones in the puncturing matrix $\mathbf{P}_l$ and $p$ denotes the puncturing period. | ||
| + | |||
| + | Starting from the rate $R_0 = 1/3$ of the mother code $\mathcal{C}_0$, we obtain: | ||
| + | * $R_1 = 8/20 = 2/5 = \underline{0.400}$, | ||
| + | * $R_2 = 8/16 = 1/2 = \underline{0.500}$, | ||
| + | * $R_3 = 8/12 = 2/3 = \underline{0.667}$, | ||
| + | * $R_4 = 8/9 = \underline{0.889}$. | ||
| + | '''(3)''' Correct are the <u>solutions 1 and 4</u>: | ||
| + | *All ones in the matrix $\mathbf{P}_4$ are also in the matrices $\mathbf{P}_3, \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, \ \mathbf{P}_0$. | ||
| + | |||
| + | *In the matrix $\mathbf{P}_3$ three ones are added compared to $\mathbf{P}_4$, in the matrix $\mathbf{P}_2$ compared to $\mathbf{P}_3$ again four, etc. | ||
| + | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^3.3 State and Trellis Diagram^]] |
Latest revision as of 14:39, 19 November 2022
An important application for $\text{punctured convolutional codes}$ are the "Rate Compatible Punctured Convolutional Codes" $($for short: RCPC–Codes$)$ proposed by Joachim Hagenauer in [Hag88].
Starting from a mother code $\mathcal{C}_0$ with rate $R_0 = 1/n$, other codes $\mathcal{C}_l$ with higher code rate $(R_l > R_0)$ are determined by different puncturing matrices $\mathbf{P}_l$.
The puncturing matrices $\mathbf{P}_0, \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \mathbf{P}_4$ to be analyzed are shown on the right.
- If for the matrix $\mathbf{P}_l$ the matrix element $P_{ij} = 1$, the corresponding code bit is transmitted, while $P_{ij} = 0$ indicates puncturing.
- In the questionnaire, we also use the shorter notation $P_{ij}^{(l)}$ for the element $P_{ij}$ of the matrix $\mathbf{P}_l$.
- In the graph: All the zeros in the matrix $\mathbf{P}_l$ that were still ones in the matrix $\mathbf{P}_{l–1}$ are marked in red. This measure increases the code rate $R_{l}$ compared to $R_{l-1}$.
The RCPC–codes are well suited for the realization of
- "unequal error protection" for hybrid ARQ procedures,
- systems with "incremental redundancy". This means that after conventional convolutional coding, bits corresponding to the puncturing matrix $\mathbf{P}_l$ are omitted from the code word $\underline{x}^{(0)}$ and the shortened code word $\underline{x}^{(l)}$ is transmitted:
- If the punctured code word cannot be correctly decoded in the receiver, the receiver requests further redundancy from the transmitter in the form of the previously punctured bits.
- This prevents the transmission of redundancy that is not required and adapts the throughput to the channel conditions.
Hints:
- This exercise refers to the section "Punctured convolutional codes" in the chapter "Code description with state and trellis diagram".
- The reference [Hag88] refers to the paper "Hagenauer, J.: Rate Compatible Punctured Convolutional Codes (RCPC codes) and their Applications. In: IEEE Transactions on Communications, vol COM-36, pp 389 - 400, 1988."
- Professor $\text{Joachim Hagenauer}$ was head of the Institute of Communications Engineering $\rm(LNT)$ at the Technical University of Munich from 1993 to 2006. The initiators of the learning tutorial $($Günter Söder and Klaus Eichin$)$ thank their long-time boss for supporting and promoting our $\rm LNTwww$ project during the first six years.
Questions
Solution
- The number of rows of the puncturing matrices gives the parameter $n$ of the $(n, \ k = 1)$ RCPC mother code.
- From this, its rate is $R_0 = 1/3$. The column number is equal to the puncturing period $p$. For the class of codes under consideration: $p = 8$.
- In contrast, the puncturing matrices do not provide any information about the memory of the code.
(2) For the rate of code $\mathcal{C}_l = p/N_l$, where $N_l$ denotes the number of all ones in the puncturing matrix $\mathbf{P}_l$ and $p$ denotes the puncturing period.
Starting from the rate $R_0 = 1/3$ of the mother code $\mathcal{C}_0$, we obtain:
- $R_1 = 8/20 = 2/5 = \underline{0.400}$,
- $R_2 = 8/16 = 1/2 = \underline{0.500}$,
- $R_3 = 8/12 = 2/3 = \underline{0.667}$,
- $R_4 = 8/9 = \underline{0.889}$.
(3) Correct are the solutions 1 and 4:
- All ones in the matrix $\mathbf{P}_4$ are also in the matrices $\mathbf{P}_3, \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, \ \mathbf{P}_0$.
- In the matrix $\mathbf{P}_3$ three ones are added compared to $\mathbf{P}_4$, in the matrix $\mathbf{P}_2$ compared to $\mathbf{P}_3$ again four, etc.