Difference between revisions of "Theory of Stochastic Signals/Poisson Distribution"
From LNTwww
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Diskrete Zufallsgrößen |Vorherige Seite=Binomialverteilung |Nächste Seite=Erzeugung von diskreten Zufallsgrößen }} ==Wahrscheinlich…“) |
|||
| Line 14: | Line 14: | ||
*Im Gegensatz zur Binomialverteilung (0 ≤ $μ$ ≤ I) kann hier die Zufallsgröße beliebig große (ganzzahlige, positive) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung. | *Im Gegensatz zur Binomialverteilung (0 ≤ $μ$ ≤ I) kann hier die Zufallsgröße beliebig große (ganzzahlige, positive) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung. | ||
*Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$: | *Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$: | ||
| − | $$p_\mu = \rm Pr (\it z=\mu) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu)!} \cdot(\frac{\lambda}{I})^\mu \cdot (\rm 1-\frac{\lambda}{I})^{I-\mu}.$$ | + | $$p_\mu = \rm Pr (\it z=\mu \rm ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot \rm (I-\mu \rm )!} \cdot\rm (\frac{\lambda}{I} \rm )^\mu \cdot \rm (\rm 1-\frac{\lambda}{I})^{I-\mu}.$$ |
Daraus erhält man nach einigen algebraischen Umformungen: | Daraus erhält man nach einigen algebraischen Umformungen: | ||
$$p_\mu = \frac{\it \lambda^\mu}{\mu!}\cdot \rm e^{-\lambda}.$$ | $$p_\mu = \frac{\it \lambda^\mu}{\mu!}\cdot \rm e^{-\lambda}.$$ | ||
| Line 23: | Line 23: | ||
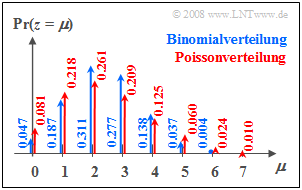
*Binomialverteilung (mit $I =$ 6, $p =$ 0.4) | *Binomialverteilung (mit $I =$ 6, $p =$ 0.4) | ||
*und Poissonverteilung (mit $λ =$ 2.4) | *und Poissonverteilung (mit $λ =$ 2.4) | ||
| + | |||
sind nebenstehender Grafik zu entnehmen: | sind nebenstehender Grafik zu entnehmen: | ||
| Line 28: | Line 29: | ||
*Bei der Poissonverteilung (rote Pfeile) sind die äußeren Werte wahrscheinlicher als bei der Binomialverteilung. | *Bei der Poissonverteilung (rote Pfeile) sind die äußeren Werte wahrscheinlicher als bei der Binomialverteilung. | ||
*Zudem sind auch Zufallsgrößen $z$ > 6 möglich, auch wenn deren Wahrscheinlichkeiten bei der gewählten Rate eher klein sind. | *Zudem sind auch Zufallsgrößen $z$ > 6 möglich, auch wenn deren Wahrscheinlichkeiten bei der gewählten Rate eher klein sind. | ||
| + | |||
| + | |||
{{end}} | {{end}} | ||
Revision as of 20:00, 26 May 2016
Wahrscheinlichkeiten der Poissonverteilung
Die Poissonverteilung ist ein Grenzfall der Binomialverteilung, wobei
- zum einen von den Grenzübergängen $I → ∞$ und $p →$ 0 ausgegangen wird,
- zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt.
Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die Rate bezeichnet. Weiter ist zu vermerken:
- Im Gegensatz zur Binomialverteilung (0 ≤ $μ$ ≤ I) kann hier die Zufallsgröße beliebig große (ganzzahlige, positive) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung.
- Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$:
$$p_\mu = \rm Pr (\it z=\mu \rm ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot \rm (I-\mu \rm )!} \cdot\rm (\frac{\lambda}{I} \rm )^\mu \cdot \rm (\rm 1-\frac{\lambda}{I})^{I-\mu}.$$ Daraus erhält man nach einigen algebraischen Umformungen: $$p_\mu = \frac{\it \lambda^\mu}{\mu!}\cdot \rm e^{-\lambda}.$$
- Binomialverteilung (mit $I =$ 6, $p =$ 0.4)
- und Poissonverteilung (mit $λ =$ 2.4)
sind nebenstehender Grafik zu entnehmen:
- Beide Verteilungen besitzen den gleichen Mittelwert $m_1 =$ 2.4.
- Bei der Poissonverteilung (rote Pfeile) sind die äußeren Werte wahrscheinlicher als bei der Binomialverteilung.
- Zudem sind auch Zufallsgrößen $z$ > 6 möglich, auch wenn deren Wahrscheinlichkeiten bei der gewählten Rate eher klein sind.