Difference between revisions of "Aufgaben:Exercise 4.08: Repetition to the Convolutional Codes"
| (7 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
[[File:P_ID3033__KC_A_4_8_v2.png|right|frame|State transition diagram of a non-recursive code]] | [[File:P_ID3033__KC_A_4_8_v2.png|right|frame|State transition diagram of a non-recursive code]] | ||
| − | The turbo codes are based on convolutional codes, which are discussed in detail in the chapter [[Channel_Coding/Basics_of_Convolutional_Coding| "Basics of Convolutional Coding"]] | + | The turbo codes are based on convolutional codes, which are discussed in detail in the chapter [[Channel_Coding/Basics_of_Convolutional_Coding| "Basics of Convolutional Coding"]]. |
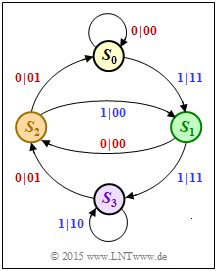
| − | Starting from the adjacent state transition diagram, essential properties and characteristics of the considered rate $1/2$ convolutional code shall be determined, and we explicitly refer to the following theory | + | Starting from the adjacent state transition diagram, essential properties and characteristics of the considered rate $1/2$ convolutional code shall be determined, and we explicitly refer to the following theory sections: |
#[[Channel_Coding/Algebraic_and_Polynomial_Description#Systematic_convolutional_codes|"Systematic convolutional codes"]] | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Systematic_convolutional_codes|"Systematic convolutional codes"]] | ||
| Line 11: | Line 11: | ||
#[[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance|"Definition of the free distance"]] | #[[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance|"Definition of the free distance"]] | ||
#[[Channel_Coding/Algebraic_and_Polynomial_Description#GF.282.29_description_forms_of_a_digital_filter|"GF(2) description forms of a digital filter"]] | #[[Channel_Coding/Algebraic_and_Polynomial_Description#GF.282.29_description_forms_of_a_digital_filter|"GF(2) description forms of a digital filter"]] | ||
| − | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Application_of_the_D.E2.80.93transform_to_rate_.7F.27.22.60UNIQ- | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Application_of_the_D.E2.80.93transform_to_rate_.7F.27.22.60UNIQ-MathJax158-QINU.60.22.27.7F_convolution_encoders| "Application of $D$–transform to rate $1/n$ convolutional codes."]] |
| − | In the state transition diagram, | + | In the state transition diagram, two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds: |
| − | * The first | + | * The first encoded bit is identical to the information bit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}.$ |
| − | * The second | + | |
| + | * The second encoded bit is the parity-check bit: $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$. | ||
| Line 25: | Line 26: | ||
Hints: | Hints: | ||
| − | * The exercise refers to the chapter [[Channel_Coding/The_Basics_of_Turbo_Codes| "Basics of Turbo Codes"]]. | + | * The exercise refers to the chapter [[Channel_Coding/The_Basics_of_Turbo_Codes| "Basics of Turbo Codes"]]. |
| + | |||
* The following semi–infinite vectors are used in the questions for this exercise: | * The following semi–infinite vectors are used in the questions for this exercise: | ||
:* information sequence $\ \underline{u} = (u_1, \, u_2, \text{ ...})$, | :* information sequence $\ \underline{u} = (u_1, \, u_2, \text{ ...})$, | ||
| − | :* parity sequence $\ \underline{p} = (p_1, \, p_2, \text{ ...})$, | + | :* parity-check sequence $\ \underline{p} = (p_1, \, p_2, \text{ ...})$, |
| − | :* impulse response $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; this is equal to the parity sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{ ...})$. | + | :* impulse response $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; this is equal to the parity-check sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{ ...})$. |
| Line 38: | Line 40: | ||
{What is the impulse response $\underline{g} $? | {What is the impulse response $\underline{g} $? | ||
|type="()"} | |type="()"} | ||
| − | - $\underline{g} = (1, \, 1, \,1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \text{ ...})$ | + | - $\underline{g} = (1, \, 1, \,1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \text{ ...})$. |
| − | + $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{ ...})$ | + | + $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{ ...})$. |
| − | {Now let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ with $u_7 ∈ \{0, \, 1\}$. Which statements are true for the parity sequence $\underline{p}$ ? | + | {Now let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ be with $u_7 ∈ \{0, \, 1\}$. Which statements are true for the parity-check sequence $\underline{p}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + The first six bits of the parity sequence are "$1, \, 0, \, 1, \, 1, \, 0, \, 1$". | + | + The first six bits of the parity-check sequence are "$1, \, 0, \, 1, \, 1, \, 0, \, 1$". |
+ With $u_7 = 0$ holds $p_i = 0$ for $i > 6$. | + With $u_7 = 0$ holds $p_i = 0$ for $i > 6$. | ||
- With $u_7 = 1$ holds $p_i = 0$ for $i > 8$. | - With $u_7 = 1$ holds $p_i = 0$ for $i > 8$. | ||
| Line 53: | Line 55: | ||
- It holds $\mathbf{G}(D) = \big [1 + D^2 \big ]$. | - It holds $\mathbf{G}(D) = \big [1 + D^2 \big ]$. | ||
| − | {Now consider the | + | {Now consider the limited input sequence $\underline{u} = (1, \, 0, \, 1, \, 0, \, 0, \, 1)$. Which statements hold for the then also limited parity-check sequence $\underline{p}$? |
|type="[]"} | |type="[]"} | ||
| − | - The first eight bits of the parity sequence are "$1, \, 0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0$. | + | - The first eight bits of the parity-check sequence are "$1, \, 0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0$". |
| − | + The first eight bits of the parity sequence are "$1, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1$". | + | + The first eight bits of the parity-check sequence are "$1, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1$". |
| − | + It holds $p_i = 0$ for $i ≥ 9$. | + | + It holds $p_i = 0$ for $i ≥ 9$. |
{What is the free distance $d_{\rm F}$ of the considered convolutional code? | {What is the free distance $d_{\rm F}$ of the considered convolutional code? | ||
| Line 66: | Line 68: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct is the <u>proposed solution 2</u>: | + | '''(1)''' Correct is the <u>proposed solution 2</u>: |
| − | *The impulse response $\underline{g}$ is equal to the output sequence $\underline{p}$ for the input sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \text{ ...})$. | + | *The impulse response $\underline{g}$ is equal to the output sequence $\underline{p}$ for the input sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \text{ ...})$. |
| − | *Based on the state $S_0$, the state transition diagram results in the following transitions: | + | |
| + | *Based on the state $S_0$, the state transition diagram results in the following transitions: | ||
:$$S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \text{ ...} \hspace{0.6cm} \Rightarrow \hspace{0.5cm} {\rm impulse\:response} \text{:} \hspace{0.2cm} \underline{g} = (1, \, 0, \, 1, \, 0, \, 0) \, .$$ | :$$S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \text{ ...} \hspace{0.6cm} \Rightarrow \hspace{0.5cm} {\rm impulse\:response} \text{:} \hspace{0.2cm} \underline{g} = (1, \, 0, \, 1, \, 0, \, 0) \, .$$ | ||
| − | *For a non-recursive filter with memory $m$ | + | *For a non-recursive filter with memory $m$ ⇒ $g_i ≡ 0$ holds for $i > m$. In our example, $m = 2$. |
| − | *In contrast, the proposed solution 1 applies to the recursive filter (RSC) corresponding to [[Aufgaben:Exercise_4.09:_Recursive_Systematic_Convolutional_Codes| | + | |
| + | *In contrast, the proposed solution 1 applies to the recursive filter $\rm (RSC)$ corresponding to [[Aufgaben:Exercise_4.09:_Recursive_Systematic_Convolutional_Codes| $\text{Exercise 4.9}$]]. | ||
| − | '''(2)''' Let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ and $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. Then the following holds for the parity sequence due to linearity: | + | '''(2)''' Let be $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ and $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. |
| + | *Then the following holds for the parity-check sequence due to linearity: | ||
:$$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | :$$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
(\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) | (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) | ||
| Line 84: | Line 89: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Correct are therefore the <u>proposed solutions 1 and 2</u> in contrast to the answer 3: | + | *Correct are therefore the <u>proposed solutions 1 and 2</u> in contrast to the answer 3: |
| − | *For $u_7 = 1$ | + | |
| + | *For $u_7 = 1$ holds $p_7 = 1, \ p_8 = 0, \ p_9 = 1$ and $p_i ≡ 0$ for $i > 9$. | ||
| + | |||
| + | |||
| + | '''(3)''' Correct is the <u>proposed solution 2</u>: | ||
| + | *From the state transition diagram one can see the code parameters $k = 1$ and $n = 2$. | ||
| + | |||
| + | *This means: The transfer function matrix $\mathbf{G}(D)$ consists of two elements ⇒ the proposition 3 is wrong. | ||
| + | * The first component of $\mathbf{G}(D)$ is actually $1$, since there is a systematic code: $\ \underline{x}^{(1)} ≡ \underline{z}$. | ||
| − | + | * The second component of $\mathbf{G}(D)$ is equal to the $D$–transform of the impulse response $\underline{g}$, where the dummy variable $D$ indicates a delay of one bit: | |
| − | * | ||
| − | |||
| − | |||
| − | |||
:$$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | :$$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
G^{(2)}(D) = 1+ D^2\hspace{0.05cm}. $$ | G^{(2)}(D) = 1+ D^2\hspace{0.05cm}. $$ | ||
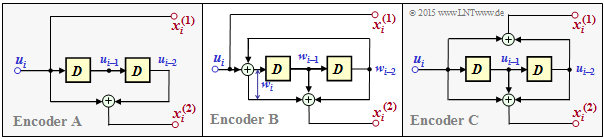
| + | [[File:EN_KC_A_4_8c_v1.png|right|frame|Three examples of rate 1/2 convolutional encoders]] | ||
| − | Going beyond the question, we also consider here the filter structure at hand | + | Going beyond the question, we also consider here the filter structure at hand. In the diagram, the encoder considered here is shown as coder $\rm A$ on the left. |
| − | + | * This is systematic like the encoder $\rm B$. But, unlike encoder $\rm B$, it is based on a non-recursive filter. | |
| − | |||
| − | + | *The encoder $\rm C$ has also a non-recursive structure, but it is not systematic. The equivalent systematic representation of encoder $\rm C$ is encoder $\rm B$. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' Correct are the <u>proposed solutions 2 and 3</u>: | + | '''(4)''' Correct are the <u>proposed solutions 2 and 3</u>: |
| − | *The exercise could be solved in the same way as subtask (2). | + | *The exercise could be solved in the same way as subtask '''(2)'''. However, we choose here for a change the way about the $D$–transform: |
| − | |||
:$$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | :$$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
U(D) = 1+ D^2 + D^5$$ | U(D) = 1+ D^2 + D^5$$ | ||
| Line 121: | Line 125: | ||
| − | '''(5)''' The free distance $d_{\rm F}$ of a convolutional encoder is equal to the minimum number of bits by which any two sequences of this code differ. | + | '''(5)''' The free distance $d_{\rm F}$ of a convolutional encoder is equal to the minimum number of bits by which any two sequences of this code differ. |
| − | *If we take as a reference the zero sequence | + | *If we take as a reference the zero sequence $\underline{0}\ \Rightarrow \ S_0 → S_0 → S_0 → S_0 → \ \text{ ...} \ $, as is commonly done then $d_{\rm F}$ is simultaneously obtained as the minimum Hamming weight $($number of "ones"$)$ of an admissible encoded sequence $\underline{x} ≠ \underline{0}$. |
| − | *From the state transition diagram, we can see that the free distance | + | *From the state transition diagram, we can see that the free distance e.g. is given by the path |
:$$ S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \text{ ...}$$ | :$$ S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \text{ ...}$$ | ||
| − | :thus identified by the | + | :thus identified by the encoded sequence $00 \hspace{0.1cm} 11 \hspace{0.1cm} 00 \hspace{0.1cm} 01 \hspace{0.1cm} 00 \text{ ...} \ .$ |
| − | *Accordingly, for the free distance of this | + | *Accordingly, for the free distance of this non-recursive code ⇒ $\hspace{0.2cm} d_{\rm F} \ \underline{= 3}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:59, 19 December 2022
The turbo codes are based on convolutional codes, which are discussed in detail in the chapter "Basics of Convolutional Coding".
Starting from the adjacent state transition diagram, essential properties and characteristics of the considered rate $1/2$ convolutional code shall be determined, and we explicitly refer to the following theory sections:
- "Systematic convolutional codes"
- "Representation in the state transition diagram"
- "Definition of the free distance"
- "GF(2) description forms of a digital filter"
- "Application of $D$–transform to rate $1/n$ convolutional codes."
In the state transition diagram, two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds:
- The first encoded bit is identical to the information bit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}.$
- The second encoded bit is the parity-check bit: $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$.
Hints:
- The exercise refers to the chapter "Basics of Turbo Codes".
- The following semi–infinite vectors are used in the questions for this exercise:
- information sequence $\ \underline{u} = (u_1, \, u_2, \text{ ...})$,
- parity-check sequence $\ \underline{p} = (p_1, \, p_2, \text{ ...})$,
- impulse response $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; this is equal to the parity-check sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{ ...})$.
Questions
Solution
- The impulse response $\underline{g}$ is equal to the output sequence $\underline{p}$ for the input sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \text{ ...})$.
- Based on the state $S_0$, the state transition diagram results in the following transitions:
- $$S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \text{ ...} \hspace{0.6cm} \Rightarrow \hspace{0.5cm} {\rm impulse\:response} \text{:} \hspace{0.2cm} \underline{g} = (1, \, 0, \, 1, \, 0, \, 0) \, .$$
- For a non-recursive filter with memory $m$ ⇒ $g_i ≡ 0$ holds for $i > m$. In our example, $m = 2$.
- In contrast, the proposed solution 1 applies to the recursive filter $\rm (RSC)$ corresponding to $\text{Exercise 4.9}$.
(2) Let be $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ and $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$.
- Then the following holds for the parity-check sequence due to linearity:
- $$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0 ,\hspace{0.05cm} 0,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...})= $$
- $$\ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...}\hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) $$
- $$\Rightarrow \hspace{0.3cm}\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.$$
- Correct are therefore the proposed solutions 1 and 2 in contrast to the answer 3:
- For $u_7 = 1$ holds $p_7 = 1, \ p_8 = 0, \ p_9 = 1$ and $p_i ≡ 0$ for $i > 9$.
(3) Correct is the proposed solution 2:
- From the state transition diagram one can see the code parameters $k = 1$ and $n = 2$.
- This means: The transfer function matrix $\mathbf{G}(D)$ consists of two elements ⇒ the proposition 3 is wrong.
- The first component of $\mathbf{G}(D)$ is actually $1$, since there is a systematic code: $\ \underline{x}^{(1)} ≡ \underline{z}$.
- The second component of $\mathbf{G}(D)$ is equal to the $D$–transform of the impulse response $\underline{g}$, where the dummy variable $D$ indicates a delay of one bit:
- $$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G^{(2)}(D) = 1+ D^2\hspace{0.05cm}. $$
Going beyond the question, we also consider here the filter structure at hand. In the diagram, the encoder considered here is shown as coder $\rm A$ on the left.
- This is systematic like the encoder $\rm B$. But, unlike encoder $\rm B$, it is based on a non-recursive filter.
- The encoder $\rm C$ has also a non-recursive structure, but it is not systematic. The equivalent systematic representation of encoder $\rm C$ is encoder $\rm B$.
(4) Correct are the proposed solutions 2 and 3:
- The exercise could be solved in the same way as subtask (2). However, we choose here for a change the way about the $D$–transform:
- $$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D^2 + D^5$$
- $$\Rightarrow \hspace{0.3cm} P(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} U(D) \cdot G(D) = (1+ D^2 + D^5) \cdot (1+ D^2 ) =1+ D^2 + D^5 + D^2 + D^4 + D^7 = 1+ D^4 + D^5 + D^7$$
- $$\Rightarrow \hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})\hspace{0.05cm}.$$
(5) The free distance $d_{\rm F}$ of a convolutional encoder is equal to the minimum number of bits by which any two sequences of this code differ.
- If we take as a reference the zero sequence $\underline{0}\ \Rightarrow \ S_0 → S_0 → S_0 → S_0 → \ \text{ ...} \ $, as is commonly done then $d_{\rm F}$ is simultaneously obtained as the minimum Hamming weight $($number of "ones"$)$ of an admissible encoded sequence $\underline{x} ≠ \underline{0}$.
- From the state transition diagram, we can see that the free distance e.g. is given by the path
- $$ S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \text{ ...}$$
- thus identified by the encoded sequence $00 \hspace{0.1cm} 11 \hspace{0.1cm} 00 \hspace{0.1cm} 01 \hspace{0.1cm} 00 \text{ ...} \ .$
- Accordingly, for the free distance of this non-recursive code ⇒ $\hspace{0.2cm} d_{\rm F} \ \underline{= 3}$.