Difference between revisions of "Exercise 3.5: Kullback-Leibler Distance and Binomial Distribution"
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables |
}} | }} | ||
[[File:EN_Inf_A_3_4_A.png|right|frame|Given probabilities]] | [[File:EN_Inf_A_3_4_A.png|right|frame|Given probabilities]] | ||
| − | We assume here the [[Theory_of_Stochastic_Signals/Binomialverteilung|binomial distribution]] | + | We assume here the [[Theory_of_Stochastic_Signals/Binomialverteilung|binomial distribution]], which is characterised by the parameters $I$ and $p$ <br>⇒ see the book [[Theory_of_Stochastic_Signals|"Theory of Stochastic Signals"]]: |
* Range of Values: | * Range of Values: | ||
| Line 15: | Line 15: | ||
* Variance: | * Variance: | ||
:$$\sigma_X^2 = I \cdot p \cdot (1-p)\hspace{0.05cm}.$$ | :$$\sigma_X^2 = I \cdot p \cdot (1-p)\hspace{0.05cm}.$$ | ||
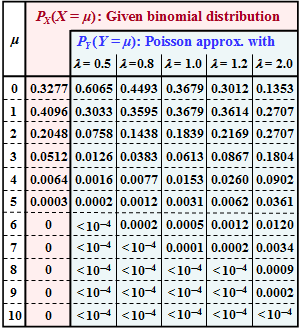
| − | In the part of the table highlighted in red, the probabilities $P_X(X = \mu$) of the binomial distribution under consideration are given. In subtask '''(1)''' you are to determine the corresponding distribution parameters $I$ and $p$ | + | In the part of the table highlighted in red, the probabilities $P_X(X = \mu$) of the binomial distribution under consideration are given. In subtask '''(1)''' you are to determine the corresponding distribution parameters $I$ and $p$. |
| − | This given binomial distribution is to be approximated here by a [[Theory_of_Stochastic_Signals/Poissonverteilung|Poisson distribution]] $Y$ | + | This given binomial distribution is to be approximated here by a [[Theory_of_Stochastic_Signals/Poissonverteilung|Poisson distribution]] $Y$, characterised by the rate $\lambda$: |
* Range of values: | * Range of values: | ||
| Line 24: | Line 24: | ||
2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm}\}\hspace{0.05cm},$$ | 2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm}\}\hspace{0.05cm},$$ | ||
* Probabilites: | * Probabilites: | ||
| − | :$$P_Y (Y = \mu) = \frac{\lambda^{\mu}}{\mu !} \cdot {\rm e}^{\lambda} \hspace{0.05cm},$$ | + | :$$P_Y (Y = \mu) = \frac{\lambda^{\mu}}{\mu !} \cdot {\rm e}^{-\lambda} \hspace{0.05cm},$$ |
* Expected values: | * Expected values: | ||
:$$m_Y = \sigma_Y^2 = \lambda\hspace{0.05cm}.$$ | :$$m_Y = \sigma_Y^2 = \lambda\hspace{0.05cm}.$$ | ||
| − | In order to assess whether the probability function $P_X(X)$ is sufficiently well approximated by $P_Y(Y)$ | + | In order to assess whether the probability mass function $P_X(X)$ is sufficiently well approximated by $P_Y(Y)$, one can resort to the so-called <b>Kullback–Leibler distances</b> $\rm (KLD)$, sometimes also called "relative entropies" in the literature. |
Adapted to the present example, these are: | Adapted to the present example, these are: | ||
| Line 34: | Line 34: | ||
[[File:EN_Inf_A_3_4_B.png|right|frame|Enclosed results table]] | [[File:EN_Inf_A_3_4_B.png|right|frame|Enclosed results table]] | ||
:$$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{\infty} P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$ | :$$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{\infty} P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$ | ||
| − | If $\log_2$ is used, the pseudo–unit | + | If $\log_2$ is used, the pseudo–unit "bit" must be added to the numerical value. |
| − | |||
| − | |||
| − | |||
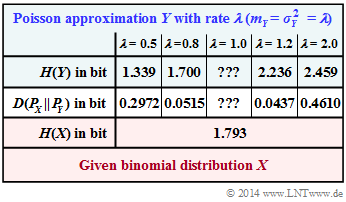
| + | In the adjacent table, the Kullback–Leibler–distance $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ (in "bit") between the binomial PMF $P_X(\cdot)$ and some Poisson approximations $P_Y(\cdot)$ $($with five different rates $\lambda)$ is entered. | ||
| + | *The respective entropy $H(Y)$, which also depends on the rate $\lambda$, is given in the first row. | ||
*The columns for $\lambda = 1$ are to be completed in subtasks '''(3)''' and '''(4)''' . | *The columns for $\lambda = 1$ are to be completed in subtasks '''(3)''' and '''(4)''' . | ||
*In subtask '''(6)''' these results are to be interpreted. | *In subtask '''(6)''' these results are to be interpreted. | ||
| Line 46: | Line 45: | ||
Hints: | Hints: | ||
| − | *The | + | *The exercise belongs to the chapter [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables|Some preliminary remarks on two-dimensional random variables]]. |
| − | *In particular, reference is made to the | + | *In particular, reference is made to the section [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Informational_divergence_-_Kullback-Leibler_distance|Relative entropy – Kullback-Leibler distance]]. |
| − | |||
*To keep the numerical calculations within limits, the following auxiliary quantities are given; here $\rm \lg$ denotes the logarithm to base $10$: | *To keep the numerical calculations within limits, the following auxiliary quantities are given; here $\rm \lg$ denotes the logarithm to base $10$: | ||
| − | :$$A' = | + | :$$A\hspace{0.05cm}' = |
0.4096 \cdot {\rm lg} \hspace{0.1cm} \frac{0.4096}{0.3679} + | 0.4096 \cdot {\rm lg} \hspace{0.1cm} \frac{0.4096}{0.3679} + | ||
0.2048 \cdot {\rm lg} \hspace{0.1cm} \frac{0.2048}{0.1839} + | 0.2048 \cdot {\rm lg} \hspace{0.1cm} \frac{0.2048}{0.1839} + | ||
| Line 56: | Line 54: | ||
0.0064 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0064}{0.0153} + | 0.0064 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0064}{0.0153} + | ||
0.0003 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0003}{0.0031} \hspace{0.05cm},$$ | 0.0003 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0003}{0.0031} \hspace{0.05cm},$$ | ||
| − | :$$B' = | + | :$$B\hspace{0.05cm}' = |
0.1839 \cdot {\rm lg} \hspace{0.1cm} (0.1839) + | 0.1839 \cdot {\rm lg} \hspace{0.1cm} (0.1839) + | ||
0.0613 \cdot {\rm lg} \hspace{0.1cm} (0.0613) + | 0.0613 \cdot {\rm lg} \hspace{0.1cm} (0.0613) + | ||
| Line 63: | Line 61: | ||
0.0005 \cdot {\rm lg} \hspace{0.1cm} (0.0005) + | 0.0005 \cdot {\rm lg} \hspace{0.1cm} (0.0005) + | ||
0.0001 \cdot {\rm lg} \hspace{0.1cm} (0.0001)$$ | 0.0001 \cdot {\rm lg} \hspace{0.1cm} (0.0001)$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm} A' \hspace{0.15cm} \underline {= 0.021944} \hspace{0.05cm},\hspace{0.5cm} | + | :$$\Rightarrow \hspace{0.3cm} A\hspace{0.05cm}' \hspace{0.15cm} \underline {= 0.021944} \hspace{0.05cm},\hspace{0.5cm} |
| − | B' \hspace{0.15cm} \underline {= -0.24717} \hspace{0.05cm}.$$ | + | B\hspace{0.05cm}' \hspace{0.15cm} \underline {= -0.24717} \hspace{0.05cm}.$$ |
| Line 70: | Line 68: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What are the characteristics of the present binomial distribution? | + | {What are the characteristics of the present binomial distribution? Hint: Enter (at most) one decimal place. |
|type="{}"} | |type="{}"} | ||
$I \hspace{0.47cm} = \ $ { 5 3% } | $I \hspace{0.47cm} = \ $ { 5 3% } | ||
| Line 86: | Line 84: | ||
| − | {Calculate the appropriate Kullback–Leibler distance $($abbreviated here as $D | + | {Calculate the appropriate Kullback–Leibler distance $($abbreviated here as $D)$ for $\lambda = 1$. Consider the auxiliary quantity $A\hspace{0.05cm}'$. |
|type="{}"} | |type="{}"} | ||
$D \ = \ $ { 0.0182 3% } $\ \rm bit$ | $D \ = \ $ { 0.0182 3% } $\ \rm bit$ | ||
| Line 98: | Line 96: | ||
{Which of the following statements are true? | {Which of the following statements are true? | ||
|type="[]"} | |type="[]"} | ||
| − | + In the $H(Y)$ calculation, all terms have the same sign. | + | + In the $H(Y)$ calculation, all terms have the same sign. |
| − | - In the $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ calculation all terms have the same sign. | + | - In the $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ calculation all terms have the same sign. |
{How do you interpret the completed results table? | {How do you interpret the completed results table? | ||
|type="[]"} | |type="[]"} | ||
| − | + According Kullback–Leibler distance, you should choose $\lambda = 1$ | + | + According Kullback–Leibler distance, you should choose $\lambda = 1$. |
- $\lambda = 1$ guarantees the best approximation $H(Y) ≈ H(X)$. | - $\lambda = 1$ guarantees the best approximation $H(Y) ≈ H(X)$. | ||
| Line 113: | Line 111: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With the binomial distribution, all probabilities are ${\rm Pr}(X > I) = 0$ ⇒ $\underline{I = 5}$. Thus, for the probability that $X =I = 5$, we get: |
:$${\rm Pr} (X = 5) = {5 \choose 5} \cdot p^{5} = p^{5} \approx 0.0003 \hspace{0.05cm}.$$ | :$${\rm Pr} (X = 5) = {5 \choose 5} \cdot p^{5} = p^{5} \approx 0.0003 \hspace{0.05cm}.$$ | ||
Thus one obtains for | Thus one obtains for | ||
| Line 127: | Line 125: | ||
*Using $D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X)$ would always result in an infinite value regardless of $λ$ since for $\mu ≥ 6$ : | *Using $D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X)$ would always result in an infinite value regardless of $λ$ since for $\mu ≥ 6$ : | ||
:$$P_X (X = \mu) = 0 \hspace{0.05cm},\hspace{0.3cm}P_Y (Y = \mu) \ne 0 \hspace{0.05cm}.$$ | :$$P_X (X = \mu) = 0 \hspace{0.05cm},\hspace{0.3cm}P_Y (Y = \mu) \ne 0 \hspace{0.05cm}.$$ | ||
| − | *Even though the probabilities $P_Y (Y = \mu)$ become very small for large $μ$ they are still | + | *Even though the probabilities $P_Y (Y = \mu)$ become very small for large $μ$ they are still "infinitely larger" than $P_X (X = \mu)$. |
| Line 134: | Line 132: | ||
'''(3)''' We use the first Kullback–Leibler distance: | '''(3)''' We use the first Kullback–Leibler distance: | ||
:$$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =\hspace{0.2cm} \sum_{\mu = 0}^{5} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm}.$$ | :$$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =\hspace{0.2cm} \sum_{\mu = 0}^{5} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm}.$$ | ||
| − | *Using the logarithm of base ten $(\lg)$  | + | *Using the logarithm of base ten $(\lg)$, we obtain for the Poisson approximation with $\lambda = 1$: |
:$$D \hspace{0.05cm}' = 0.3277 \cdot {\rm lg} \hspace{0.1cm} \frac{0.3277}{0.3679} + A \hspace{0.05cm}' = | :$$D \hspace{0.05cm}' = 0.3277 \cdot {\rm lg} \hspace{0.1cm} \frac{0.3277}{0.3679} + A \hspace{0.05cm}' = | ||
-0.016468 + 0.021944 = 0.005476 \hspace{0.05cm}.$$ | -0.016468 + 0.021944 = 0.005476 \hspace{0.05cm}.$$ | ||
| Line 144: | Line 142: | ||
:$$H\hspace{0.05cm}'(Y) = -{\rm E} \left [{\rm lg} \hspace{0.1cm} {P_Y(Y)} \right ] | :$$H\hspace{0.05cm}'(Y) = -{\rm E} \left [{\rm lg} \hspace{0.1cm} {P_Y(Y)} \right ] | ||
= -2 \cdot 0.3679 \cdot {\rm lg} \hspace{0.1cm} (0.3679) - B\hspace{0.05cm}' = 0.31954 + 0.24717 = 0.56126.$$ | = -2 \cdot 0.3679 \cdot {\rm lg} \hspace{0.1cm} (0.3679) - B\hspace{0.05cm}' = 0.31954 + 0.24717 = 0.56126.$$ | ||
| − | *Converting to | + | *Converting to "bit" gives the result we are looking for: |
:$$H(Y) = \frac{0.56126}{{\rm lg} \hspace{0.1cm}(2)} | :$$H(Y) = \frac{0.56126}{{\rm lg} \hspace{0.1cm}(2)} | ||
\hspace{0.15cm} \underline {= 1.864\ {\rm (bit)}} \hspace{0.05cm}.$$ | \hspace{0.15cm} \underline {= 1.864\ {\rm (bit)}} \hspace{0.05cm}.$$ | ||
| Line 151: | Line 149: | ||
'''(5)''' Correct is <u>statement 1</u>. In the numerical calculation of the Kullback–Leibler distance | '''(5)''' Correct is <u>statement 1</u>. In the numerical calculation of the Kullback–Leibler distance | ||
| − | * the contribution of the $μ$–th term is positive if $P_Y(\mu) > P_X(\mu)$, | + | * the contribution of the $μ$–th term is positive, if $P_Y(\mu) > P_X(\mu)$, |
| − | * the contribution of the $μ$–th term is negative if $P_Y(\mu) < P_X(\mu)$. | + | * the contribution of the $μ$–th term is negative, if $P_Y(\mu) < P_X(\mu)$. |
| Line 167: | Line 165: | ||
* With $λ = 1$ , the <u>linear means</u> of the two random variables coincide: | * With $λ = 1$ , the <u>linear means</u> of the two random variables coincide: | ||
:$$m_X = m_Y= 1.$$ | :$$m_X = m_Y= 1.$$ | ||
| − | * With $λ = 0.9$ the <u> | + | * With $λ = 0.9$ the <u>second moments</u> agree: |
:$$m_X + \sigma_X^2 = m_Y + \sigma_Y^2= 1.8.$$ | :$$m_X + \sigma_X^2 = m_Y + \sigma_Y^2= 1.8.$$ | ||
| − | Whether this statement is relevant, we leave undecided. Because: Due to the steady increase of $H(Y)$ with increasing $λ$ , it is clear that for some $λ$–value $H(Y) = H(X)$ must indeed hold. | + | Whether this statement is relevant, we leave undecided. |
| + | |||
| + | Because: Due to the steady increase of $H(Y)$ with increasing $λ$ , it is clear that for some $λ$–value $H(Y) = H(X)$ must indeed hold. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:19, 18 January 2023
We assume here the binomial distribution, which is characterised by the parameters $I$ and $p$
⇒ see the book "Theory of Stochastic Signals":
- Range of Values:
- $$X = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.15cm} 1\hspace{0.05cm},\hspace{0.15cm} 2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} I\hspace{0.05cm}\}\hspace{0.05cm},$$
- Probabilities:
- $$P_X (X = \mu) = {I \choose \mu} \cdot p^{\mu} \cdot (1-p)^{I-\mu} \hspace{0.05cm},$$
- Linear mean:
- $$m_X = I \cdot p \hspace{0.05cm},$$
- Variance:
- $$\sigma_X^2 = I \cdot p \cdot (1-p)\hspace{0.05cm}.$$
In the part of the table highlighted in red, the probabilities $P_X(X = \mu$) of the binomial distribution under consideration are given. In subtask (1) you are to determine the corresponding distribution parameters $I$ and $p$.
This given binomial distribution is to be approximated here by a Poisson distribution $Y$, characterised by the rate $\lambda$:
- Range of values:
- $$Y = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.15cm} 1\hspace{0.05cm},\hspace{0.05cm} 2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm}\}\hspace{0.05cm},$$
- Probabilites:
- $$P_Y (Y = \mu) = \frac{\lambda^{\mu}}{\mu !} \cdot {\rm e}^{-\lambda} \hspace{0.05cm},$$
- Expected values:
- $$m_Y = \sigma_Y^2 = \lambda\hspace{0.05cm}.$$
In order to assess whether the probability mass function $P_X(X)$ is sufficiently well approximated by $P_Y(Y)$, one can resort to the so-called Kullback–Leibler distances $\rm (KLD)$, sometimes also called "relative entropies" in the literature.
Adapted to the present example, these are:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{I} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm},$$
- $$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{\infty} P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$
If $\log_2$ is used, the pseudo–unit "bit" must be added to the numerical value.
In the adjacent table, the Kullback–Leibler–distance $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ (in "bit") between the binomial PMF $P_X(\cdot)$ and some Poisson approximations $P_Y(\cdot)$ $($with five different rates $\lambda)$ is entered.
- The respective entropy $H(Y)$, which also depends on the rate $\lambda$, is given in the first row.
- The columns for $\lambda = 1$ are to be completed in subtasks (3) and (4) .
- In subtask (6) these results are to be interpreted.
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
- In particular, reference is made to the section Relative entropy – Kullback-Leibler distance.
- To keep the numerical calculations within limits, the following auxiliary quantities are given; here $\rm \lg$ denotes the logarithm to base $10$:
- $$A\hspace{0.05cm}' = 0.4096 \cdot {\rm lg} \hspace{0.1cm} \frac{0.4096}{0.3679} + 0.2048 \cdot {\rm lg} \hspace{0.1cm} \frac{0.2048}{0.1839} + 0.0512 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0512}{0.0613} + 0.0064 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0064}{0.0153} + 0.0003 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0003}{0.0031} \hspace{0.05cm},$$
- $$B\hspace{0.05cm}' = 0.1839 \cdot {\rm lg} \hspace{0.1cm} (0.1839) + 0.0613 \cdot {\rm lg} \hspace{0.1cm} (0.0613) + 0.0153 \cdot {\rm lg} \hspace{0.1cm} (0.0153) + 0.0031 \cdot {\rm lg} \hspace{0.1cm} (0.0031) + 0.0005 \cdot {\rm lg} \hspace{0.1cm} (0.0005) + 0.0001 \cdot {\rm lg} \hspace{0.1cm} (0.0001)$$
- $$\Rightarrow \hspace{0.3cm} A\hspace{0.05cm}' \hspace{0.15cm} \underline {= 0.021944} \hspace{0.05cm},\hspace{0.5cm} B\hspace{0.05cm}' \hspace{0.15cm} \underline {= -0.24717} \hspace{0.05cm}.$$
Questions
Solution
- $${\rm Pr} (X = 5) = {5 \choose 5} \cdot p^{5} = p^{5} \approx 0.0003 \hspace{0.05cm}.$$
Thus one obtains for
- the characteristic probability: $p= (0.0003)^{1/5} = 0.1974 \hspace{0.15cm} \underline {\approx 0.2}\hspace{0.05cm},$
- the linear mean (expected value): $m_X = I \cdot p \hspace{0.15cm} \underline {= 1}\hspace{0.05cm},$
- the variance: $\sigma_X^2 = I \cdot p \cdot (1-p) \hspace{0.15cm} \underline {= 0.8}\hspace{0.05cm}.$
(2) Proposed solution 2 is correct:
- Using $D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X)$ would always result in an infinite value regardless of $λ$ since for $\mu ≥ 6$ :
- $$P_X (X = \mu) = 0 \hspace{0.05cm},\hspace{0.3cm}P_Y (Y = \mu) \ne 0 \hspace{0.05cm}.$$
- Even though the probabilities $P_Y (Y = \mu)$ become very small for large $μ$ they are still "infinitely larger" than $P_X (X = \mu)$.
(3) We use the first Kullback–Leibler distance:
- $$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =\hspace{0.2cm} \sum_{\mu = 0}^{5} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm}.$$
- Using the logarithm of base ten $(\lg)$, we obtain for the Poisson approximation with $\lambda = 1$:
- $$D \hspace{0.05cm}' = 0.3277 \cdot {\rm lg} \hspace{0.1cm} \frac{0.3277}{0.3679} + A \hspace{0.05cm}' = -0.016468 + 0.021944 = 0.005476 \hspace{0.05cm}.$$
- After converting to the logarithm of base two $(\log_2)$ , we finally obtain:
- $$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{0.005476}{{\rm lg} \hspace{0.1cm}(2)} \hspace{0.15cm} \underline {\approx 0.0182\ {\rm (bit)}}\hspace{0.05cm}.$$
(4) Using the logarithm of base ten, the entropy of the Poisson approximation $(\lambda = 1)$:
- $$H\hspace{0.05cm}'(Y) = -{\rm E} \left [{\rm lg} \hspace{0.1cm} {P_Y(Y)} \right ] = -2 \cdot 0.3679 \cdot {\rm lg} \hspace{0.1cm} (0.3679) - B\hspace{0.05cm}' = 0.31954 + 0.24717 = 0.56126.$$
- Converting to "bit" gives the result we are looking for:
- $$H(Y) = \frac{0.56126}{{\rm lg} \hspace{0.1cm}(2)} \hspace{0.15cm} \underline {= 1.864\ {\rm (bit)}} \hspace{0.05cm}.$$
(5) Correct is statement 1. In the numerical calculation of the Kullback–Leibler distance
- the contribution of the $μ$–th term is positive, if $P_Y(\mu) > P_X(\mu)$,
- the contribution of the $μ$–th term is negative, if $P_Y(\mu) < P_X(\mu)$.
(6) Proposed solution 1 is correct:
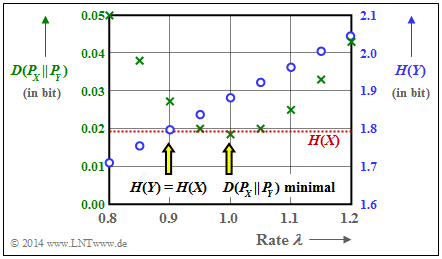
- It can also be seen from the graph that $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =0.0182$ bit is not undercut by any $λ$–value other than $λ = 1$ (green crosses).
- Furthermore, one can see from this plot that a better entropy approximation is achieved with $λ = 0.9$ than with $λ = 1$ (blue circles):
- $$H(Y) = 1.795\ {\rm bit} \hspace{0.15cm}\approx \hspace{0.15cm} H(X) = 1.793\ {\rm bit}\hspace{0.05cm}.$$
- The second proposed solution is therefore wrong.
- With $λ = 1$ , the linear means of the two random variables coincide:
- $$m_X = m_Y= 1.$$
- With $λ = 0.9$ the second moments agree:
- $$m_X + \sigma_X^2 = m_Y + \sigma_Y^2= 1.8.$$
Whether this statement is relevant, we leave undecided.
Because: Due to the steady increase of $H(Y)$ with increasing $λ$ , it is clear that for some $λ$–value $H(Y) = H(X)$ must indeed hold.