Difference between revisions of "Aufgaben:Exercise 4.7: Spectra of ASK and BPSK"
| Line 58: | Line 58: | ||
|type="[]"} | |type="[]"} | ||
+ The continuous part of $ {\it Φ}_q(f)$ is equal in form to $|G_q(f)|^2$. | + The continuous part of $ {\it Φ}_q(f)$ is equal in form to $|G_q(f)|^2$. | ||
| − | - ${\it Φ}_q(f)$ contains a single Dirac line at ASK for BPSK $($at $f = 0)$. | + | - ${\it Φ}_q(f)$ contains a single Dirac delta line at ASK for BPSK $($at $f = 0)$. |
| − | - ${\it Φ}_q(f)$ contains a single Dirac line at BPSK for BPSK $($at $f = 0)$. | + | - ${\it Φ}_q(f)$ contains a single Dirac delta line at BPSK for BPSK $($at $f = 0)$. |
</quiz> | </quiz> | ||
| Line 76: | Line 76: | ||
'''(2)''' The spectrum $Z(f)$ of a cosine signal $z(t)$ consists of two Dirac delta functions at $\pm f_{\rm T}$, each with weight $1/2$. | '''(2)''' The spectrum $Z(f)$ of a cosine signal $z(t)$ consists of two Dirac delta functions at $\pm f_{\rm T}$, each with weight $1/2$. | ||
| − | *The power-spectral density ${\it Φ}_z(f)$ also consists of the two Dirac delta | + | *The power-spectral density ${\it Φ}_z(f)$ also consists of the two Dirac delta functions, but now with respective weights $1/4$. |
*The convolution ${\it Φ}_q(f) ∗ {\it Φ}_z(f)$ gives the power-spectral density ${\it Φ}_s(f)$ of the transmitted signal. It follows that: | *The convolution ${\it Φ}_q(f) ∗ {\it Φ}_z(f)$ gives the power-spectral density ${\it Φ}_s(f)$ of the transmitted signal. It follows that: | ||
:$$C = {A}/{4} \hspace{0.15cm}\underline { = 0.25 \cdot 10^{-6} \,{\rm | :$$C = {A}/{4} \hspace{0.15cm}\underline { = 0.25 \cdot 10^{-6} \,{\rm | ||
| Line 92: | Line 92: | ||
'''(3)''' For BPSK, the source signal $q(t)$ is to be bipolar. | '''(3)''' For BPSK, the source signal $q(t)$ is to be bipolar. | ||
| − | *Therefore, the Dirac line is missing in the power-spectral density ⇒ $\underline{B = 0}$. | + | *Therefore, the Dirac delta line is missing in the power-spectral density ⇒ $\underline{B = 0}$. |
* The continuous PSD component is four times larger than with ASK: | * The continuous PSD component is four times larger than with ASK: | ||
:$$A = {s_0^2 \cdot T }\hspace{0.15cm}\underline { = 4 \cdot 10^{-6} \,{\rm V^{2}/Hz}}.$$ | :$$A = {s_0^2 \cdot T }\hspace{0.15cm}\underline { = 4 \cdot 10^{-6} \,{\rm V^{2}/Hz}}.$$ | ||
| Line 105: | Line 105: | ||
'''(5)''' Only the <u>first statement</u> is correct: | '''(5)''' Only the <u>first statement</u> is correct: | ||
| − | * For BPSK, ${\it Φ}_q(f)$ does not contain a single Dirac line even if $g_q(t)$ deviates from the rectangular form (assuming equally probable symbols). | + | * For BPSK, ${\it Φ}_q(f)$ does not contain a single Dirac delta line even if $g_q(t)$ deviates from the rectangular form (assuming equally probable symbols). |
| − | *In contrast, the unipolar ASK source signal contains infinitely many Dirac lines at all multiples of $1/T$. | + | *In contrast, the unipolar ASK source signal contains infinitely many Dirac delta lines at all multiples of $1/T$. |
*For more information on this topic, see the page "ACF and PSD for unipolar binary signals" in the book "Digital Signal Transmission". | *For more information on this topic, see the page "ACF and PSD for unipolar binary signals" in the book "Digital Signal Transmission". | ||
Latest revision as of 13:31, 18 January 2023
The transmitted signals of $\rm ASK$ ("Amplitude Shift Keying") and $\rm BPSK$ ("Binary Phase Shift Keying") can both be expressed in the form
- $$s(t) = q(t) · z(t),$$
where the carrier $z(t)$ represents a harmonic oscillation with frequency $f_{\rm T}$ and amplitude $1$. The carrier phase $ϕ_{\rm T}$ is not important for the power-spectral densities considered here.
- In each case, the source is redundancy-free, which means that the two possible symbols are equally probable and the symbols are statistically independent of each other.
- For ASK, the unipolar amplitude coefficients – that is: $a_ν ∈ \{0, 1\}$ – of the source signal are
- $$ q(t) = \sum_{\nu = - \infty}^{+\infty}a_\nu \cdot g_q (t - \nu \cdot T)$$
- while in the case of BPSK $a_ν ∈ \{-1, +1\}$ has to be considered.
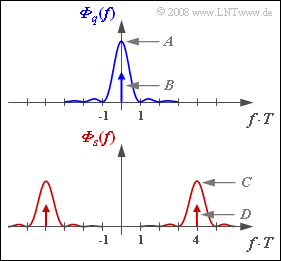
In the diagram, the power-spectral densities ${\it Φ}_q(f)$ and ${\it Φ}_s(f)$ of the source signal and the transmitted signal are given, respectively, for an NRZ rectangular pulse $g_q(t)$ with amplitude $s_0 = 2 \ \rm V$ and duration $T = 1 \ \rm µ s$. Thus the spectral function is:
- $$G_q(f) = s_0 \cdot T \cdot {\rm si}(\pi f T)\hspace{0.05cm}.$$
The constants $A$, $B$, $C$ and $D$ for the $\rm ASK$ and $\rm BPSK$ modulation methods are to be determined.
Notes:
- The exercise belongs to the chapter Linear Digital Modulation.
- Reference is also made to the chapter Basics of Coded Transmission in the book "Digital Signal Transmission".
- The powers are to be specified in $\rm V^2$; they thus refer to the reference resistance $R = 1 \ \rm \Omega$.
Questions
Solution
- Without this DC component, the stochastic signal $q(t) - m_q ∈ \{+s_0/2, -s_0/2\}$ would be obtained.
- This DC-free signal has the continuous PSD component $(s_0/2)^2 · T · {\rm sinc}^2(fT)$.
- From this, the value we are looking for at frequency $f = 0$ can be determined:
- $$A = \frac {s_0^2 \cdot T }{4} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{4}\hspace{0.15cm}\underline {= 10^{-6} \,{\rm V^{2}/Hz}}.$$
(2) The spectrum $Z(f)$ of a cosine signal $z(t)$ consists of two Dirac delta functions at $\pm f_{\rm T}$, each with weight $1/2$.
- The power-spectral density ${\it Φ}_z(f)$ also consists of the two Dirac delta functions, but now with respective weights $1/4$.
- The convolution ${\it Φ}_q(f) ∗ {\it Φ}_z(f)$ gives the power-spectral density ${\it Φ}_s(f)$ of the transmitted signal. It follows that:
- $$C = {A}/{4} \hspace{0.15cm}\underline { = 0.25 \cdot 10^{-6} \,{\rm V^{2}/Hz}},\hspace{0.2cm}D = {B}/{4}\hspace{0.15cm}\underline { = 0.25 \,{\rm V^{2}}}.$$
Note: The power per bit is obtained as the integral over ${\it Φ}_s(f)$:
- $$P_{\rm S} = \int_{ - \infty }^\infty \hspace{-0.3cm} {{\it \Phi}_s(f)}\hspace{0.1cm} {\rm d}f = 2 \cdot \int_{ 0 }^\infty \hspace{-0.3cm} {\left [ C \cdot {\rm sinc}^2(f T) + D \cdot \delta (f - f_{\rm T}]\right ]}\hspace{0.1cm} {\rm d}f= 2 \cdot \left [ \frac{C}{T} + D \right ] = 2 \cdot \left [ \frac{0.25 \cdot 10^{-6} \,{\rm V^{2}/Hz}}{10^{-6} \,{\rm s}} + 0.25 \,{\rm V^{2}} \right ] \hspace{0.15cm}\underline {= 1 \,{\rm V^{2}}}.$$
(3) For BPSK, the source signal $q(t)$ is to be bipolar.
- Therefore, the Dirac delta line is missing in the power-spectral density ⇒ $\underline{B = 0}$.
- The continuous PSD component is four times larger than with ASK:
- $$A = {s_0^2 \cdot T }\hspace{0.15cm}\underline { = 4 \cdot 10^{-6} \,{\rm V^{2}/Hz}}.$$
(4) For the PSD parameters of the BPSK transmitted signal, the following applies analogously to the ASK:
- $$C = \frac {A}{4}\hspace{0.15cm}\underline { = 10^{-6} \,{\rm V^{2}/Hz}},\hspace{0.2cm}D = \frac {B}{4} \hspace{0.15cm}\underline {= 0}.$$
(5) Only the first statement is correct:
- For BPSK, ${\it Φ}_q(f)$ does not contain a single Dirac delta line even if $g_q(t)$ deviates from the rectangular form (assuming equally probable symbols).
- In contrast, the unipolar ASK source signal contains infinitely many Dirac delta lines at all multiples of $1/T$.
- For more information on this topic, see the page "ACF and PSD for unipolar binary signals" in the book "Digital Signal Transmission".