Difference between revisions of "Aufgaben:Exercise 4.2Z: Multiplication with a Sine Signal"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Differences_and_Similarities_of_Low-Pass_and_Band-Pass_Signals |
}} | }} | ||
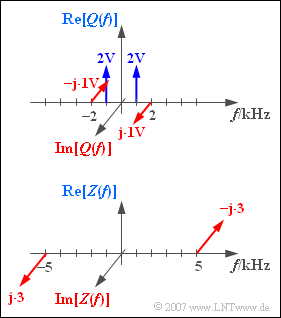
[[File:P_ID697__Sig_Z_4_2_neu.png|right|frame|Spectral functions $Q(f)$ and $Z(f)$]] | [[File:P_ID697__Sig_Z_4_2_neu.png|right|frame|Spectral functions $Q(f)$ and $Z(f)$]] | ||
| − | A periodic message signal $q(t)$is considered, whose spectral function $Q(f)$ can be seen in the upper graph. | + | A periodic message signal $q(t)$ is considered, whose spectral function $Q(f)$ can be seen in the upper graph. |
A multiplication with the dimensionless carrier $z(t)$, whose spectrum $Z(f)$ is also shown, leads to the signal $s(t) = q(t) \cdot z(t).$ | A multiplication with the dimensionless carrier $z(t)$, whose spectrum $Z(f)$ is also shown, leads to the signal $s(t) = q(t) \cdot z(t).$ | ||
| Line 17: | Line 17: | ||
''Hint:'' | ''Hint:'' | ||
| − | *This exercise belongs to the | + | *This exercise belongs to the chapter [[Signal_Representation/Differences_and_Similarities_of_Low-Pass_and_Band-Pass_Signals|Differences and Similarities of Low-Pass and Band-Pass Signals]]. |
| Line 26: | Line 26: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Give the source signal $q(t)$ in analytical form. Which values result for $t = 0$ und $t = 0.125\, \text{ms}$? | + | {Give the source signal $q(t)$ in analytical form. Which values result for $t = 0$ und $t = 0.125\, \text{ms}$? |
|type="{}"} | |type="{}"} | ||
$q(t = 0)\ = \ $ { 4 3% } $\text{V}$ | $q(t = 0)\ = \ $ { 4 3% } $\text{V}$ | ||
| Line 32: | Line 32: | ||
| − | {What is the (dimensionless) carrier signal $z(t)$? What is its maximum value? | + | {What is the (dimensionless) carrier signal $z(t)$? What is its maximum value? |
|type="{}"} | |type="{}"} | ||
$z_{\rm max}\ = \ $ { 6 3% } | $z_{\rm max}\ = \ $ { 6 3% } | ||
| − | {Calculate the spectrum $S(f)$ separately for real and imaginary parts. At which frequencies are there lines with a non-zero real part? | + | {Calculate the spectrum $S(f)$ separately for real and imaginary parts. At which frequencies are there lines with a non-zero real part? |
|type="[]"} | |type="[]"} | ||
+ $3\ \text{kHz},$ | + $3\ \text{kHz},$ | ||
| Line 61: | Line 61: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The | + | '''(1)''' The source signal can be represented with the abbreviations $f_1 = 1\ \text{kHz}$ and $T_1 = 1/f_1 = 1 \ \text{ms}$ as follows $($ $f_2 = 2f_1 applies)$: |
:$$q(t ) = 4\hspace{0.05cm}{\rm V} | :$$q(t ) = 4\hspace{0.05cm}{\rm V} | ||
\cdot {\cos} ( 2 \pi f_1 t) - 2\hspace{0.05cm}{\rm V} | \cdot {\cos} ( 2 \pi f_1 t) - 2\hspace{0.05cm}{\rm V} | ||
| Line 82: | Line 82: | ||
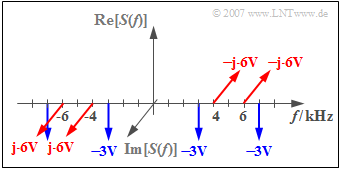
| − | [[File:EN_Sig_Z_4_2_c_neu.png|right|frame|Discrete | + | [[File:EN_Sig_Z_4_2_c_neu.png|right|frame|Discrete band-pass spectrum]] |
'''(3)''' The spectral function $S(f)$ results from the convolution between $Q(f)$ and $Z(f)$. One obtains: | '''(3)''' The spectral function $S(f)$ results from the convolution between $Q(f)$ and $Z(f)$. One obtains: | ||
:$$S(f) = - 3{\rm j} \cdot Q(f- f_{\rm T}) + 3{\rm j} \cdot Q(f+ | :$$S(f) = - 3{\rm j} \cdot Q(f- f_{\rm T}) + 3{\rm j} \cdot Q(f+ | ||
| Line 99: | Line 99: | ||
| − | '''(4)''' Imaginary lines appear at $\underline{\pm 4 \ \text{kHz}}$ <u>and</u> $\underline{\pm 6 \ \text{kHz}}$ | + | '''(4)''' Imaginary lines appear at $\underline{\pm 4 \ \text{kHz}}$ <u>and</u> $\underline{\pm 6 \ \text{kHz}}$. |
An alternative way to solve this problem is to use trigonometric equations. | An alternative way to solve this problem is to use trigonometric equations. | ||
| − | In the following, for example, $f_5 = 5 \text{ kHz}$. Then it applies: | + | In the following, for example, $f_5 = 5 \text{ kHz}$. Then it applies: |
:$$4\hspace{0.05cm}{\rm V} | :$$4\hspace{0.05cm}{\rm V} | ||
\cdot {\cos} ( 2 \pi f_1 \hspace{0.03cm}t) \cdot 3 | \cdot {\cos} ( 2 \pi f_1 \hspace{0.03cm}t) \cdot 3 | ||
| Line 121: | Line 121: | ||
:* at $+f_6$ and $-f_6$ with weights $–{\rm j} \cdot 3 \ {\rm V}$ bzw. $+{\rm j} \cdot 3 \ {\rm V}$ respectively. | :* at $+f_6$ and $-f_6$ with weights $–{\rm j} \cdot 3 \ {\rm V}$ bzw. $+{\rm j} \cdot 3 \ {\rm V}$ respectively. | ||
| − | *The second equation gives a total of four | + | *The second equation gives a total of four Dirac delta lines (all $6 \ {\rm V}$, real and negative) at $\pm f_3$ and $\pm f_7$. |
| Line 129: | Line 129: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^4.1 Differences between Low-Pass and Band-Pass^]] |
Latest revision as of 14:21, 18 January 2023
A periodic message signal $q(t)$ is considered, whose spectral function $Q(f)$ can be seen in the upper graph.
A multiplication with the dimensionless carrier $z(t)$, whose spectrum $Z(f)$ is also shown, leads to the signal $s(t) = q(t) \cdot z(t).$
In this task, the spectral function $S(f)$ of this signal is to be determined, whereby the solution can be either in the time or frequency domain.
Hint:
- This exercise belongs to the chapter Differences and Similarities of Low-Pass and Band-Pass Signals.
Questions
Solution
- $$q(t ) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_1 t) - 2\hspace{0.05cm}{\rm V} \cdot {\sin} ( 4 \pi f_1 t)= 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi {t}/{T_1}) - 2\hspace{0.05cm}{\rm V} \cdot {\sin} ( 4 \pi {t}/{T_1}) .$$
- At time $t = 0$ , the second component disappears and $q(t = 0)\; \underline{= 4 \ \text{V}}$.
- On the other hand, for $t = 0.125 \ \text{ms} = T_1/8$ is obtained:
- $$q(t = 0.125{\rm ms}) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( {\pi}/{4}) - 2\hspace{0.05cm}{\rm V} \cdot {\sin} ( {\pi}/{2}) = \frac {4\hspace{0.05cm}{\rm V}}{\sqrt{2}} - 2\hspace{0.05cm}{\rm V} \hspace{0.15 cm}\underline{= 0.828 \hspace{0.05cm}{\rm V}}.$$
(2) According to the purely imaginary spectrum $Z(f)$ and the impulse weights $\pm 3$ must hold:
- $$z(t ) = 6 \cdot {\sin} ( 2 \pi \cdot 5\hspace{0.05cm}{\rm kHz})\hspace{0.5cm}\Rightarrow \hspace{0.5cm} z_{\rm max}\hspace{0.15 cm}\underline{ = 6} .$$
(3) The spectral function $S(f)$ results from the convolution between $Q(f)$ and $Z(f)$. One obtains:
- $$S(f) = - 3{\rm j} \cdot Q(f- f_{\rm T}) + 3{\rm j} \cdot Q(f+ f_{\rm T}).$$
This results in spectral lines at
- $3\ \text{kHz}\ (–3\ {\rm V})$,
- $4\ \text{kHz} (–{\rm j} \cdot 6\ {\rm V})$,
- $6\ \text{kHz} (–{\rm j} \cdot 6\ {\rm V})$,
- $7\ \text{kHz}\ (–3\ {\rm V})$.
Plus the conjugate-complex components at negative frequencies.
Lines with real weights at $\underline{\pm 3 \ \text{kHz}}$ and $\underline{\pm 7 \ \text{kHz}}$.
(4) Imaginary lines appear at $\underline{\pm 4 \ \text{kHz}}$ and $\underline{\pm 6 \ \text{kHz}}$.
An alternative way to solve this problem is to use trigonometric equations.
In the following, for example, $f_5 = 5 \text{ kHz}$. Then it applies:
- $$4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_1 \hspace{0.03cm}t) \cdot 3 \cdot {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)= \frac{12\hspace{0.05cm}{\rm V}}{2}\cdot \big[{\sin} ( 2 \pi f_4 \hspace{0.03cm} t)+ {\sin} ( 2 \pi f_6 \hspace{0.03cm} t)\big],$$
- $$-2\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi f_2 \hspace{0.03cm}t) \cdot 3 \cdot {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)= \frac{-6\hspace{0.05cm}{\rm V}}{2}\cdot \big[{\cos} ( 2 \pi f_3 \hspace{0.03cm} t)+ {\cos} ( 2 \pi f_7 \hspace{0.03cm} t)\big].$$
- From the first equation, the following spectral lines are obtained:
- at $+f_4$ and $-f_4$ with weights $–{\rm j} \cdot 3\ {\rm V}$ bzw. $+{\rm j}\cdot 3 \ {\rm V}$ respectively,
- at $+f_6$ and $-f_6$ with weights $–{\rm j} \cdot 3 \ {\rm V}$ bzw. $+{\rm j} \cdot 3 \ {\rm V}$ respectively.
- The second equation gives a total of four Dirac delta lines (all $6 \ {\rm V}$, real and negative) at $\pm f_3$ and $\pm f_7$.
A comparison with the sketch above shows that both solutions lead to the same result.