Difference between revisions of "Aufgaben:Exercise 2.3: DSB-AM Realization"
| (13 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
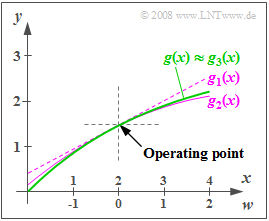
| − | [[File:EN_Mod_A_2_3.png|right|frame| | + | [[File:EN_Mod_A_2_3.png|right|frame|Nonlinear characteristic curve <br>for DSB-AM realization]] |
| − | + | In order to realize the so-called "Double-Sideband Amplitude Modulation $\text{(DSB-AM)}$ with carrier", an amplifier with the following characteristic curve must be used: | |
:$$y = g(x) = U \cdot \left( 1 -{\rm e} ^{-x/U}\right)$$ | :$$y = g(x) = U \cdot \left( 1 -{\rm e} ^{-x/U}\right)$$ | ||
| − | + | *Here, $x = x(t)$ and $y = y(t)$ are time-dependent voltages at the input and output of the amplifier, respectively. | |
| + | *The parameter $U = 3 \ \rm V$ indicates the saturation voltage of the amplifier. | ||
| − | + | ||
| + | This curve is used at the operating point $A_0 = 2\ \rm V$. This is achieved, for example, by the input signal | ||
:$$x(t) = A_0 + z(t) + q(t)\hspace{0.05cm}.$$ | :$$x(t) = A_0 + z(t) + q(t)\hspace{0.05cm}.$$ | ||
| − | + | Assume cosine oscillations for both the carrier and the source signal: | |
:$$ z(t) = A_{\rm T} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} A_{\rm T} = 1\,{\rm V},\hspace{0.2cm} f_{\rm T} = 30\,{\rm kHz},$$ | :$$ z(t) = A_{\rm T} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} A_{\rm T} = 1\,{\rm V},\hspace{0.2cm} f_{\rm T} = 30\,{\rm kHz},$$ | ||
:$$ q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} A_{\rm N} = 1\,{\rm V},\hspace{0.2cm} f_{\rm N} = 3\,{\rm kHz}\hspace{0.05cm}.$$ | :$$ q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} A_{\rm N} = 1\,{\rm V},\hspace{0.2cm} f_{\rm N} = 3\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| − | + | In solving this problem, use the auxiliary quantity | |
:$$w(t) = x(t) - A_0 = z(t) + q(t)\hspace{0.05cm}.$$ | :$$w(t) = x(t) - A_0 = z(t) + q(t)\hspace{0.05cm}.$$ | ||
| − | + | The nonlinear characteristic curve can be developed according to a "Taylor series" around the operating point: | |
:$$y(x) = y(A_0) + \frac{1}{1!} \cdot y\hspace{0.08cm}{\rm '}(A_0) \cdot (x - A_0)+ \frac{1}{2!} \cdot y\hspace{0.08cm}''(A_0) \cdot (x - A_0)^2+ | :$$y(x) = y(A_0) + \frac{1}{1!} \cdot y\hspace{0.08cm}{\rm '}(A_0) \cdot (x - A_0)+ \frac{1}{2!} \cdot y\hspace{0.08cm}''(A_0) \cdot (x - A_0)^2+ | ||
\frac{1}{3!} \cdot y\hspace{0.08cm}'''(A_0) \cdot (x - A_0)^3 + \text{ ...}$$ | \frac{1}{3!} \cdot y\hspace{0.08cm}'''(A_0) \cdot (x - A_0)^3 + \text{ ...}$$ | ||
| − | + | The output signal can then also be represented as depending on the auxiliary quantity $w(t)$ as follows: | |
:$$y(t) = c_0 + c_1 \cdot w(t) + c_2 \cdot w^2(t)+ c_3 \cdot w^3(t) +\text{ ...}$$ | :$$y(t) = c_0 + c_1 \cdot w(t) + c_2 \cdot w^2(t)+ c_3 \cdot w^3(t) +\text{ ...}$$ | ||
| − | + | *The DSB–AM signal $s(t)$ is obtained by band-limiting $y(t)$ to the frequency range from $\text{23 kHz}$ to $\text{37 kHz}$. | |
| − | + | *That is, all frequencies other than $f_{\rm T}$, $f_{\rm T}±f_{\rm N}$ and $f_{\rm T}±2f_{\rm N}$ are removed by the band-pass. | |
| − | |||
| − | |||
| − | |||
| + | The graph shows the characteristic curve $g(x)$ and the approximations $g_1(x)$, $g_2(x)$ and $g_3(x)$, when the Taylor series is truncated after the first, second, or third term. It can be seen that the approximation $g_3(x)$ is indistinguishable from $g(x)$ in the range shown. | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Double-Sideband_Amplitude_Modulation|Double-Sideband Amplitude Modulation]]. |
| − | * | + | *Reference will also be made to the chapter [[Linear_and_Time_Invariant_Systems/Nonlinear_Distortions#Description_of_nonlinear_systems|Description of nonlinear systems]] in the book "Linear and Time Invariant Systems". |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | {In | + | {In what range can the input signal $x(t)$ vary? Give the minimum and maximum values of the auxiliary variable $w(t) = x(t) - A_0$. |
|type="{}"} | |type="{}"} | ||
$w_{\rm min} \ = \ $ { -2.06--1.94 } $\ \text{V}$ | $w_{\rm min} \ = \ $ { -2.06--1.94 } $\ \text{V}$ | ||
$w_{\rm max} \ = \ ${ 2 3% }$\ \text{V}$ | $w_{\rm max} \ = \ ${ 2 3% }$\ \text{V}$ | ||
| − | { | + | {Calculate the coefficients $c_0$ and $c_1$ of the Taylor series. |
|type="{}"} | |type="{}"} | ||
$c_0 \ = \ $ { 1.46 3% } $\ \text{V}$ | $c_0 \ = \ $ { 1.46 3% } $\ \text{V}$ | ||
$c_1 \ = \ $ { 0.513 3% } | $c_1 \ = \ $ { 0.513 3% } | ||
| − | { | + | {What are the coefficients $c_2$ and $c_3$ of the nonlinear characteristic curve? |
|type="{}"} | |type="{}"} | ||
$c_2\ = \ $ { -0.088--0.084 } $\ \rm V^{ -1 }$ | $c_2\ = \ $ { -0.088--0.084 } $\ \rm V^{ -1 }$ | ||
$c_3\ = \ $ { 0.0095 3% } $\ \rm V^{ -2 }$ | $c_3\ = \ $ { 0.0095 3% } $\ \rm V^{ -2 }$ | ||
| − | { | + | {Show that a "DSB-AM with carrier" constellation results when $c_3$ is considered negligibly small. What is the modulation depth $m$? |
|type="{}"} | |type="{}"} | ||
$m \ = \ $ { 0.335 3% } | $m \ = \ $ { 0.335 3% } | ||
| − | { | + | {Assuming that $c_3$ cannot be considered negligibly small, which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The weight of the spectral line at $f_{\rm T}$ is unchanged. |
| − | + $s(t)$ | + | + $s(t)$ now includes Dirac delta lines at $f_{\rm T} ± 2f_{\rm N}$. |
| − | + | + | + The cubic term leads to nonlinear distortions. |
| − | - | + | - The cubic term leads to linear distortions. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From $x(t) = A_0 + z(t) + q(t)$, with $A_0 = 2\ \rm V$ and $A_{\rm T} = A_{\rm N} = 1 \ \rm V$, we get the possible range $0 \ {\rm V} ≤ x(t) ≤ 4\ \rm V$. |
| − | * | + | *Thus, the auxiliary quantity $w(t)$ can take values between $w_{\rm min}\hspace{0.15cm}\underline{ = -2 \ \rm V}$ and $w_{\rm max}\hspace{0.15cm}\underline{ = +2 \ \rm V}$. |
| − | '''(2)''' | + | '''(2)''' The coefficient $c_0$ is equal to the characteristic value at the operating point. Using $A_0 = 2 \ \rm V$ and $U = 3 \ \rm V$ we obtain: |
:$$c_0 = y(A_0) = U \cdot \left( 1 -{\rm e} ^{-A_0/U}\right) \hspace{0.15cm}\underline {= 1.460\,{\rm V}}\hspace{0.05cm}.$$ | :$$c_0 = y(A_0) = U \cdot \left( 1 -{\rm e} ^{-A_0/U}\right) \hspace{0.15cm}\underline {= 1.460\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | * | + | *Accordingly, for the Taylor coefficient $c_1$: |
:$$c_1 = y\hspace{0.06cm}'(A_0)= {\rm e} ^{-A_0/U}\hspace{0.15cm}\underline { = 0.513}\hspace{0.05cm}.$$ | :$$c_1 = y\hspace{0.06cm}'(A_0)= {\rm e} ^{-A_0/U}\hspace{0.15cm}\underline { = 0.513}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The further derivatives $(n ≥ 2)$ are: |
:$$y^{(n)}(A_0)= \frac{(-1)^{n-1}}{U^{n-1}} \cdot {\rm e} ^{-A_0/U} \hspace{0.05cm}.$$ | :$$y^{(n)}(A_0)= \frac{(-1)^{n-1}}{U^{n-1}} \cdot {\rm e} ^{-A_0/U} \hspace{0.05cm}.$$ | ||
| − | * | + | *This results in the following coefficients: |
:$$ c_2 = \frac{1}{2!} \cdot y^{(2)}(A_0)= \frac{1}{2U} \cdot {\rm e}^{-A_0/U} \hspace{0.15cm}\underline {= -0.086\,{\rm V^{-1}}}\hspace{0.05cm},$$ | :$$ c_2 = \frac{1}{2!} \cdot y^{(2)}(A_0)= \frac{1}{2U} \cdot {\rm e}^{-A_0/U} \hspace{0.15cm}\underline {= -0.086\,{\rm V^{-1}}}\hspace{0.05cm},$$ | ||
:$$c_3 = \frac{1}{3!} \cdot y^{(3)}(A_0)= \frac{1}{6U^2} \cdot {\rm e}^{-A_0/U}\hspace{0.15cm}\underline { = 0.0095\,{\rm V^{-2}}}\hspace{0.05cm}.$$ | :$$c_3 = \frac{1}{3!} \cdot y^{(3)}(A_0)= \frac{1}{6U^2} \cdot {\rm e}^{-A_0/U}\hspace{0.15cm}\underline { = 0.0095\,{\rm V^{-2}}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Setting $c_3 = 0$, the output signal of the amplifier is: |
:$$y(t) = c_0 + c_1 \cdot (z(t) + q(t)) + c_2 \cdot (z^2(t) + q^2(t) + 2 \cdot z(t) \cdot q(t))\hspace{0.05cm}.$$ | :$$y(t) = c_0 + c_1 \cdot (z(t) + q(t)) + c_2 \cdot (z^2(t) + q^2(t) + 2 \cdot z(t) \cdot q(t))\hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, after the band-pass, the following signal components remain: |
:$$s(t) = c_1 \cdot z(t) + 2 \cdot c_2 \cdot z(t) \cdot q(t) | :$$s(t) = c_1 \cdot z(t) + 2 \cdot c_2 \cdot z(t) \cdot q(t) | ||
= \left[c_1 \cdot A_{\rm T} + 2 \cdot c_2 \cdot A_{\rm T} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} t)\right] \cdot \cos(\omega_{\rm T} t)\hspace{0.05cm}.$$ | = \left[c_1 \cdot A_{\rm T} + 2 \cdot c_2 \cdot A_{\rm T} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} t)\right] \cdot \cos(\omega_{\rm T} t)\hspace{0.05cm}.$$ | ||
| − | * | + | *The modulation depth is then determined as the quotient of the "amplitude of the message oscillation" over the "amplitude of the carrier": |
:$$m = \frac{2 \cdot |c_2| \cdot A_{\rm T} \cdot A_{\rm N}}{|c_1| \cdot A_{\rm T}} = \frac{2 \cdot |c_2| \cdot A_{\rm N}}{|c_1| }= \frac{2 \cdot 0.086 \cdot 1\,{\rm V}}{0.513 }\hspace{0.15cm}\underline { = 0.335}\hspace{0.05cm}.$$ | :$$m = \frac{2 \cdot |c_2| \cdot A_{\rm T} \cdot A_{\rm N}}{|c_1| \cdot A_{\rm T}} = \frac{2 \cdot |c_2| \cdot A_{\rm N}}{|c_1| }= \frac{2 \cdot 0.086 \cdot 1\,{\rm V}}{0.513 }\hspace{0.15cm}\underline { = 0.335}\hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' <u>Answers 2 and 3</u> are correct: |
| − | * | + | *Considering the cubic part, $y(t)$ includes the following other components: |
:$$y_3(t) = c_3 \cdot (z(t) + q(t))^3 | :$$y_3(t) = c_3 \cdot (z(t) + q(t))^3 | ||
= c_3 \cdot z^3(t) + 3 \cdot c_3 \cdot z^2(t) \cdot q(t)+ 3 \cdot c_3 \cdot z(t) \cdot q^2(t) + c_3 \cdot q^3(t) \hspace{0.05cm}.$$ | = c_3 \cdot z^3(t) + 3 \cdot c_3 \cdot z^2(t) \cdot q(t)+ 3 \cdot c_3 \cdot z(t) \cdot q^2(t) + c_3 \cdot q^3(t) \hspace{0.05cm}.$$ | ||
| − | * | + | *The first term results in components at $f_{\rm T}$ and $3f_{\rm T}$, and the last term results in components at $f_{\rm N}$ and $3f_{\rm N}$. |
| + | *The second term gives a component at $f_{\rm N}$ and others at $2f_{\rm T} ± f_{\rm N}$: | ||
:$$3 \cdot c_3 \cdot z^2(t) \cdot q(t)= {3}/{2 } \cdot A_{\rm T}^2 \cdot A_{\rm N} \cdot \left[ \cos(\omega_{\rm N} t) + \cos(2\omega_{\rm T} t) \cdot \cos(\omega_{\rm N} t)\right] \hspace{0.05cm}.$$ | :$$3 \cdot c_3 \cdot z^2(t) \cdot q(t)= {3}/{2 } \cdot A_{\rm T}^2 \cdot A_{\rm N} \cdot \left[ \cos(\omega_{\rm N} t) + \cos(2\omega_{\rm T} t) \cdot \cos(\omega_{\rm N} t)\right] \hspace{0.05cm}.$$ | ||
| − | * | + | *Accordingly, the third summand in the above equation leads to |
:$$3 \cdot c_3 \cdot z(t) \cdot q^2(t)= {3}/{2 } \cdot A_{\rm T} \cdot A_{\rm N}^2 \cdot \left[ \cos(\omega_{\rm T} t) + \cos(\omega_{\rm T} t)\cdot \cos(2 \omega_{\rm N} t)\right] \hspace{0.05cm}.$$ | :$$3 \cdot c_3 \cdot z(t) \cdot q^2(t)= {3}/{2 } \cdot A_{\rm T} \cdot A_{\rm N}^2 \cdot \left[ \cos(\omega_{\rm T} t) + \cos(\omega_{\rm T} t)\cdot \cos(2 \omega_{\rm N} t)\right] \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, within the frequency range from $\text{23 kHz}$ to $\text{37 kHz}$, there is indeed a change in the spectral line at $f_{\rm T}$ <br>and new Dirac delta lines are formed at $f_{\rm T} ± 2f_{\rm N}$, i.e., at $\text{24 kHz}$ and $\text{36 kHz}$. |
| − | * | + | *The resulting distortions are thus nonlinear ⇒ Answer 3 ist correct and Answer 4 is wrong. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 114: | Line 115: | ||
| − | [[Category:Modulation Methods: Exercises|^2.1 | + | [[Category:Modulation Methods: Exercises|^2.1 Double Sideband Amplitude Modulation^]] |
Latest revision as of 15:18, 18 January 2023
In order to realize the so-called "Double-Sideband Amplitude Modulation $\text{(DSB-AM)}$ with carrier", an amplifier with the following characteristic curve must be used:
- $$y = g(x) = U \cdot \left( 1 -{\rm e} ^{-x/U}\right)$$
- Here, $x = x(t)$ and $y = y(t)$ are time-dependent voltages at the input and output of the amplifier, respectively.
- The parameter $U = 3 \ \rm V$ indicates the saturation voltage of the amplifier.
This curve is used at the operating point $A_0 = 2\ \rm V$. This is achieved, for example, by the input signal
- $$x(t) = A_0 + z(t) + q(t)\hspace{0.05cm}.$$
Assume cosine oscillations for both the carrier and the source signal:
- $$ z(t) = A_{\rm T} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} A_{\rm T} = 1\,{\rm V},\hspace{0.2cm} f_{\rm T} = 30\,{\rm kHz},$$
- $$ q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} A_{\rm N} = 1\,{\rm V},\hspace{0.2cm} f_{\rm N} = 3\,{\rm kHz}\hspace{0.05cm}.$$
In solving this problem, use the auxiliary quantity
- $$w(t) = x(t) - A_0 = z(t) + q(t)\hspace{0.05cm}.$$
The nonlinear characteristic curve can be developed according to a "Taylor series" around the operating point:
- $$y(x) = y(A_0) + \frac{1}{1!} \cdot y\hspace{0.08cm}{\rm '}(A_0) \cdot (x - A_0)+ \frac{1}{2!} \cdot y\hspace{0.08cm}''(A_0) \cdot (x - A_0)^2+ \frac{1}{3!} \cdot y\hspace{0.08cm}'''(A_0) \cdot (x - A_0)^3 + \text{ ...}$$
The output signal can then also be represented as depending on the auxiliary quantity $w(t)$ as follows:
- $$y(t) = c_0 + c_1 \cdot w(t) + c_2 \cdot w^2(t)+ c_3 \cdot w^3(t) +\text{ ...}$$
- The DSB–AM signal $s(t)$ is obtained by band-limiting $y(t)$ to the frequency range from $\text{23 kHz}$ to $\text{37 kHz}$.
- That is, all frequencies other than $f_{\rm T}$, $f_{\rm T}±f_{\rm N}$ and $f_{\rm T}±2f_{\rm N}$ are removed by the band-pass.
The graph shows the characteristic curve $g(x)$ and the approximations $g_1(x)$, $g_2(x)$ and $g_3(x)$, when the Taylor series is truncated after the first, second, or third term. It can be seen that the approximation $g_3(x)$ is indistinguishable from $g(x)$ in the range shown.
Hints:
- This exercise belongs to the chapter Double-Sideband Amplitude Modulation.
- Reference will also be made to the chapter Description of nonlinear systems in the book "Linear and Time Invariant Systems".
Questions
Solution
- Thus, the auxiliary quantity $w(t)$ can take values between $w_{\rm min}\hspace{0.15cm}\underline{ = -2 \ \rm V}$ and $w_{\rm max}\hspace{0.15cm}\underline{ = +2 \ \rm V}$.
(2) The coefficient $c_0$ is equal to the characteristic value at the operating point. Using $A_0 = 2 \ \rm V$ and $U = 3 \ \rm V$ we obtain:
- $$c_0 = y(A_0) = U \cdot \left( 1 -{\rm e} ^{-A_0/U}\right) \hspace{0.15cm}\underline {= 1.460\,{\rm V}}\hspace{0.05cm}.$$
- Accordingly, for the Taylor coefficient $c_1$:
- $$c_1 = y\hspace{0.06cm}'(A_0)= {\rm e} ^{-A_0/U}\hspace{0.15cm}\underline { = 0.513}\hspace{0.05cm}.$$
(3) The further derivatives $(n ≥ 2)$ are:
- $$y^{(n)}(A_0)= \frac{(-1)^{n-1}}{U^{n-1}} \cdot {\rm e} ^{-A_0/U} \hspace{0.05cm}.$$
- This results in the following coefficients:
- $$ c_2 = \frac{1}{2!} \cdot y^{(2)}(A_0)= \frac{1}{2U} \cdot {\rm e}^{-A_0/U} \hspace{0.15cm}\underline {= -0.086\,{\rm V^{-1}}}\hspace{0.05cm},$$
- $$c_3 = \frac{1}{3!} \cdot y^{(3)}(A_0)= \frac{1}{6U^2} \cdot {\rm e}^{-A_0/U}\hspace{0.15cm}\underline { = 0.0095\,{\rm V^{-2}}}\hspace{0.05cm}.$$
(4) Setting $c_3 = 0$, the output signal of the amplifier is:
- $$y(t) = c_0 + c_1 \cdot (z(t) + q(t)) + c_2 \cdot (z^2(t) + q^2(t) + 2 \cdot z(t) \cdot q(t))\hspace{0.05cm}.$$
- Thus, after the band-pass, the following signal components remain:
- $$s(t) = c_1 \cdot z(t) + 2 \cdot c_2 \cdot z(t) \cdot q(t) = \left[c_1 \cdot A_{\rm T} + 2 \cdot c_2 \cdot A_{\rm T} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} t)\right] \cdot \cos(\omega_{\rm T} t)\hspace{0.05cm}.$$
- The modulation depth is then determined as the quotient of the "amplitude of the message oscillation" over the "amplitude of the carrier":
- $$m = \frac{2 \cdot |c_2| \cdot A_{\rm T} \cdot A_{\rm N}}{|c_1| \cdot A_{\rm T}} = \frac{2 \cdot |c_2| \cdot A_{\rm N}}{|c_1| }= \frac{2 \cdot 0.086 \cdot 1\,{\rm V}}{0.513 }\hspace{0.15cm}\underline { = 0.335}\hspace{0.05cm}.$$
(5) Answers 2 and 3 are correct:
- Considering the cubic part, $y(t)$ includes the following other components:
- $$y_3(t) = c_3 \cdot (z(t) + q(t))^3 = c_3 \cdot z^3(t) + 3 \cdot c_3 \cdot z^2(t) \cdot q(t)+ 3 \cdot c_3 \cdot z(t) \cdot q^2(t) + c_3 \cdot q^3(t) \hspace{0.05cm}.$$
- The first term results in components at $f_{\rm T}$ and $3f_{\rm T}$, and the last term results in components at $f_{\rm N}$ and $3f_{\rm N}$.
- The second term gives a component at $f_{\rm N}$ and others at $2f_{\rm T} ± f_{\rm N}$:
- $$3 \cdot c_3 \cdot z^2(t) \cdot q(t)= {3}/{2 } \cdot A_{\rm T}^2 \cdot A_{\rm N} \cdot \left[ \cos(\omega_{\rm N} t) + \cos(2\omega_{\rm T} t) \cdot \cos(\omega_{\rm N} t)\right] \hspace{0.05cm}.$$
- Accordingly, the third summand in the above equation leads to
- $$3 \cdot c_3 \cdot z(t) \cdot q^2(t)= {3}/{2 } \cdot A_{\rm T} \cdot A_{\rm N}^2 \cdot \left[ \cos(\omega_{\rm T} t) + \cos(\omega_{\rm T} t)\cdot \cos(2 \omega_{\rm N} t)\right] \hspace{0.05cm}.$$
- Thus, within the frequency range from $\text{23 kHz}$ to $\text{37 kHz}$, there is indeed a change in the spectral line at $f_{\rm T}$
and new Dirac delta lines are formed at $f_{\rm T} ± 2f_{\rm N}$, i.e., at $\text{24 kHz}$ and $\text{36 kHz}$. - The resulting distortions are thus nonlinear ⇒ Answer 3 ist correct and Answer 4 is wrong.