Difference between revisions of "Aufgaben:Exercise 3.4Z: Continuous Phase Frequency Shift Keying"
| (7 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
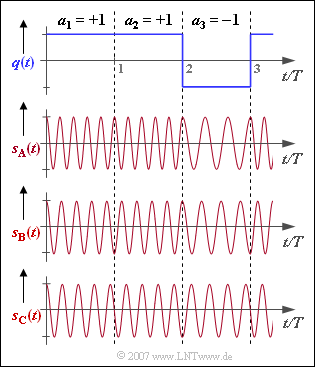
| − | [[File:P_ID1231__Bei_Z_3_4.png|right|frame|Signals for $\ | + | [[File:P_ID1231__Bei_Z_3_4.png|right|frame|Signals for $\text{CP-FSK}$]] |
| − | The graph shows three FSK | + | The graph shows three frequency shift keying $\rm (FSK)$ transmitted signals which differ with respect to the frequency deviation $\Delta f_{\rm A}$ distinguish and thus also by their modulation index |
| − | :$$h = 2 \cdot \Delta f_{\rm A} \cdot T$$ | + | :$$h = 2 \cdot \Delta f_{\rm A} \cdot T.$$ |
| − | + | ||
| − | The digital source signal $q(t)$ underlying the signals $s_{\rm A}(t), s_{\rm B}(t)$ and $s_{\rm C}(t)$ is shown above. All considered signals are normalized to amplitude $1$ and time duration $T$ and | + | The digital source signal $q(t)$ underlying the signals $s_{\rm A}(t), s_{\rm B}(t)$ and $s_{\rm C}(t)$ is shown above. All considered signals are normalized to amplitude $1$ and time duration $T$ and based on a cosine carrier with frequency $f_{\rm T}$. |
| − | With binary FSK ( | + | With binary FSK $($"Binary Frequency Shift Keying"$)$ only two different frequencies occur, each of which remains constant over a bit duration: |
*$f_{1}$ $($if $a_{\nu} = +1)$, | *$f_{1}$ $($if $a_{\nu} = +1)$, | ||
| − | |||
| + | *$f_{2}$ $($if $a_{\nu} = -1)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | If the modulation index is not a multiple of $2$, continuous phase adjustment is required to avoid phase jumps. This is called "Continuous Phase Frequency Shift Keying" $(\text{CP-FSK)}$. | ||
| + | An important special case is represented by binary FSK with modulation index $h = 0.5$ which is also called "Minimum Shift Keying" $(\rm MSK)$. This will be discussed in this exercise. | ||
| + | <u>Hints:</u> | ||
| + | *This exercise belongs to the chapter [[Examples_of_Communication_Systems/Radio_Interface|"Radio Interface"]]. | ||
| − | + | *Reference is made in particular to the section [[Examples_of_Communication_Systems/Radio_Interface#Continuous_phase_adjustment_with_FSK|"Continuous phase adjustment with FSK]]. | |
| − | |||
| − | *Reference is made in particular to the | ||
| − | |||
| − | |||
===Questions=== | ===Questions=== | ||
| Line 39: | Line 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true for FSK and specifically for MSK? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + FSK is generally a nonlinear modulation method. |
| − | + | + | + MSK can be implemented as offset QPSK and is therefore linear. |
| − | - | + | - This results in the same bit error rate as for QPSK. |
| − | + | + | + A band limitation is less disturbing than with QPSK. |
| − | + | + | + The MSK envelope is constant even with spectral shaping. |
| − | { | + | {What frequencies $f_{1}$ $($for amplitude coefficient $a_{\nu} = +1)$ and $f_{2}$ $($for $a_{\nu} = -1)$ does the signal $s_{\rm A}(t)$ contain? |
|type="{}"} | |type="{}"} | ||
$f_{1} \cdot T \ = \ $ { 5 3% } | $f_{1} \cdot T \ = \ $ { 5 3% } | ||
$f_{2} \cdot T \ = \ $ { 3 3% } | $f_{2} \cdot T \ = \ $ { 3 3% } | ||
| − | { | + | {What are the carrier frequency $f_{\rm T}$, the frequency deviation $\Delta f_{\rm A}$ and the modulation index $h$ for signal $s_{\rm A}(t)$? |
|type="{}"} | |type="{}"} | ||
$f_{\rm T} \cdot T \ = \ $ { 4 3% } | $f_{\rm T} \cdot T \ = \ $ { 4 3% } | ||
| Line 58: | Line 53: | ||
$h \ = \ $ { 2 3% } | $h \ = \ $ { 2 3% } | ||
| − | { | + | {What is the modulation index for signal $s_{\rm B}(t)$? |
|type="{}"} | |type="{}"} | ||
$h \ = \ $ { 1 3% } | $h \ = \ $ { 1 3% } | ||
| − | { | + | {What is the modulation index for signal $s_{\rm C}(t)$? |
|type="{}"} | |type="{}"} | ||
$h \ = \ $ { 0.5 3% } | $h \ = \ $ { 0.5 3% } | ||
| − | { | + | {Which signals required continuous phase adjustment? |
|type="[]"} | |type="[]"} | ||
- $s_{\rm A}(t)$, | - $s_{\rm A}(t)$, | ||
| Line 72: | Line 67: | ||
+ $s_{\rm C}(t)$. | + $s_{\rm C}(t)$. | ||
| − | { | + | {What signals describe "Minimum Shift Keying" $\rm (MSK)$? |
|type="[]"} | |type="[]"} | ||
- $s_{\rm A}(t)$, | - $s_{\rm A}(t)$, | ||
| Line 81: | Line 76: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u> | + | '''(1)''' <u>All statements except the third are true</u>: |
| − | * | + | *Generally nonlinear FSK can only be demodulated coherently, while MSK can also use a noncoherent demodulation method. |
| − | * | + | |
| − | + | *Compared to QPSK with coherent demodulation, MSK requires $3 \ \rm dB$ more $E_{\rm B}/N_{0}$ $($energy per bit related to the noise power density$)$ for the same bit error rate. | |
| − | |||
| + | *The first zero in the power-spectral density occurs in MSK later than in QSPK, but it shows a faster asymptotic decay than in QSPK. | ||
| + | |||
| + | *The constant envelope of MSK means that nonlinearities in the transmission line do not play a role. This allows the use of simple and inexpensive power amplifiers with lower power consumption and thus longer operating times of battery-powered devices. | ||
| − | '''(2)''' | + | |
| + | '''(2)''' One can see from the graph five and three oscillations per symbol duration, respectively: | ||
:$$f_{\rm 1} \cdot T \hspace{0.15cm} \underline {= 5}\hspace{0.05cm},\hspace{0.2cm}f_{\rm 2} \cdot T \hspace{0.15cm} \underline { = 3}\hspace{0.05cm}.$$ | :$$f_{\rm 1} \cdot T \hspace{0.15cm} \underline {= 5}\hspace{0.05cm},\hspace{0.2cm}f_{\rm 2} \cdot T \hspace{0.15cm} \underline { = 3}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' For FSK with rectangular pulse shape, only the two instantaneous frequencies $f_{1} = f_{\rm T} + \Delta f_{\rm A}$ and $f_{2} = f_{\rm T} - \Delta f_{\rm A}$ occur. |
| − | * | + | *With the result from subtask '''(2)''' we thus obtain: |
:$$f_{\rm T} \ = \ \frac{f_{\rm 1}+f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm T} \cdot T \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$ | :$$f_{\rm T} \ = \ \frac{f_{\rm 1}+f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm T} \cdot T \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$ | ||
:$$ \Delta f_{\rm A} \ = \ \frac{f_{\rm 1}-f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline { = 1}\hspace{0.05cm},$$ | :$$ \Delta f_{\rm A} \ = \ \frac{f_{\rm 1}-f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline { = 1}\hspace{0.05cm},$$ | ||
| Line 103: | Line 101: | ||
| − | '''(4)''' | + | '''(4)''' From the graph one can see the frequencies $f_{1} \cdot T = 4.5$ and $f_{2} \cdot T = 3.5$. |
| − | * | + | *This results in the frequency deviation $\Delta f_{\rm A} \cdot T = 0.5$ and the modulation index $\underline{h = 1}$. |
| − | '''(5)''' | + | '''(5)''' Here the two $($normalized$)$ frequencies $f_{1} \cdot T = 4.25$ and $f_{2} \cdot T = 3.75$ occur, |
| − | * | + | *which results in the frequency deviation $\Delta f_{\rm A} \cdot T = 0.25$ and the modulation index $\underline{h = 0.5}$. |
| − | '''(6)''' | + | '''(6)''' Correct are the <u>solutions 2 and 3</u>: |
| − | * | + | *Only at $s_{\rm A}(t)$ was no phase adjustment made. Here, the signal waveforms in the region of the first and second bit $(a_{1} = a_{2} = +1)$ are each cosinusoidal like the carrier signal $($with respect to the symbol boundary$)$. |
| − | + | ||
| − | * | + | *In contrast, in the second symbol of $s_{\rm B}(t)$ a minus-cosine-shaped course $($initial phase $\phi_{0} = π$, corresponding to $180^\circ)$ can be seen and in the second symbol of $s_{\rm C}(t)$ a minus-sine-shaped course $(\phi_{0} = π /2$ or $90^\circ)$. |
| − | * | + | |
| + | *For $s_{\rm A}(t)$ the initial phase is always zero, for $s_{\rm B}(t)$ either zero or $π$, while for the signal $s_{\rm C}(t)$ with modulation index $h = 0.5$ a total of four initial phases are possible: $0^\circ, \ 90^\circ, \ 180^\circ$ and $270^\circ$. | ||
| − | '''(7)''' | + | '''(7)''' Correct is the <u>last proposed solution</u>, since for this signal ⇒ $h = 0.5$. |
| − | * | + | *This is the smallest possible modulation index for which there is orthogonality between $f_{1}$ and $f_{2}$ within the symbol duration $T$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:21, 22 January 2023
The graph shows three frequency shift keying $\rm (FSK)$ transmitted signals which differ with respect to the frequency deviation $\Delta f_{\rm A}$ distinguish and thus also by their modulation index
- $$h = 2 \cdot \Delta f_{\rm A} \cdot T.$$
The digital source signal $q(t)$ underlying the signals $s_{\rm A}(t), s_{\rm B}(t)$ and $s_{\rm C}(t)$ is shown above. All considered signals are normalized to amplitude $1$ and time duration $T$ and based on a cosine carrier with frequency $f_{\rm T}$.
With binary FSK $($"Binary Frequency Shift Keying"$)$ only two different frequencies occur, each of which remains constant over a bit duration:
- $f_{1}$ $($if $a_{\nu} = +1)$,
- $f_{2}$ $($if $a_{\nu} = -1)$.
If the modulation index is not a multiple of $2$, continuous phase adjustment is required to avoid phase jumps. This is called "Continuous Phase Frequency Shift Keying" $(\text{CP-FSK)}$.
An important special case is represented by binary FSK with modulation index $h = 0.5$ which is also called "Minimum Shift Keying" $(\rm MSK)$. This will be discussed in this exercise.
Hints:
- This exercise belongs to the chapter "Radio Interface".
- Reference is made in particular to the section "Continuous phase adjustment with FSK.
Questions
Solution
- Generally nonlinear FSK can only be demodulated coherently, while MSK can also use a noncoherent demodulation method.
- Compared to QPSK with coherent demodulation, MSK requires $3 \ \rm dB$ more $E_{\rm B}/N_{0}$ $($energy per bit related to the noise power density$)$ for the same bit error rate.
- The first zero in the power-spectral density occurs in MSK later than in QSPK, but it shows a faster asymptotic decay than in QSPK.
- The constant envelope of MSK means that nonlinearities in the transmission line do not play a role. This allows the use of simple and inexpensive power amplifiers with lower power consumption and thus longer operating times of battery-powered devices.
(2) One can see from the graph five and three oscillations per symbol duration, respectively:
- $$f_{\rm 1} \cdot T \hspace{0.15cm} \underline {= 5}\hspace{0.05cm},\hspace{0.2cm}f_{\rm 2} \cdot T \hspace{0.15cm} \underline { = 3}\hspace{0.05cm}.$$
(3) For FSK with rectangular pulse shape, only the two instantaneous frequencies $f_{1} = f_{\rm T} + \Delta f_{\rm A}$ and $f_{2} = f_{\rm T} - \Delta f_{\rm A}$ occur.
- With the result from subtask (2) we thus obtain:
- $$f_{\rm T} \ = \ \frac{f_{\rm 1}+f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm T} \cdot T \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$
- $$ \Delta f_{\rm A} \ = \ \frac{f_{\rm 1}-f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline { = 1}\hspace{0.05cm},$$
- $$h \ = \ 2 \cdot \Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$
(4) From the graph one can see the frequencies $f_{1} \cdot T = 4.5$ and $f_{2} \cdot T = 3.5$.
- This results in the frequency deviation $\Delta f_{\rm A} \cdot T = 0.5$ and the modulation index $\underline{h = 1}$.
(5) Here the two $($normalized$)$ frequencies $f_{1} \cdot T = 4.25$ and $f_{2} \cdot T = 3.75$ occur,
- which results in the frequency deviation $\Delta f_{\rm A} \cdot T = 0.25$ and the modulation index $\underline{h = 0.5}$.
(6) Correct are the solutions 2 and 3:
- Only at $s_{\rm A}(t)$ was no phase adjustment made. Here, the signal waveforms in the region of the first and second bit $(a_{1} = a_{2} = +1)$ are each cosinusoidal like the carrier signal $($with respect to the symbol boundary$)$.
- In contrast, in the second symbol of $s_{\rm B}(t)$ a minus-cosine-shaped course $($initial phase $\phi_{0} = π$, corresponding to $180^\circ)$ can be seen and in the second symbol of $s_{\rm C}(t)$ a minus-sine-shaped course $(\phi_{0} = π /2$ or $90^\circ)$.
- For $s_{\rm A}(t)$ the initial phase is always zero, for $s_{\rm B}(t)$ either zero or $π$, while for the signal $s_{\rm C}(t)$ with modulation index $h = 0.5$ a total of four initial phases are possible: $0^\circ, \ 90^\circ, \ 180^\circ$ and $270^\circ$.
(7) Correct is the last proposed solution, since for this signal ⇒ $h = 0.5$.
- This is the smallest possible modulation index for which there is orthogonality between $f_{1}$ and $f_{2}$ within the symbol duration $T$.