Radio Interface

1 Logical channels of GSM
2 Uplink and downlink parameters
3 Realization of FDMA and TDMA
4 The different burst types in GSM
5 GSM frame structure
6 Modulation in GSM systems
7 Continuous phase adjustment with FSK
8 Minimum Shift Keying (MSK)
9 Gaussian Minimum Shift Keying (GMSK)
10 Advantages and disadvantages of GMSK
11 Radio Subsystem Link Control
12 Exercises for the chapter
13 References

Logical channels of GSM

The »radio interface« is crucial for the proper operation of the GSM network and the exchange of information between mobile and base station.

This is also called the "air interface" or "physical layer" and defines all physical channels of the GSM system as well as their assignment to the logical channels.

Furthermore, the radio interface is responsible for other functionalities such as the "radio subsystem link control".

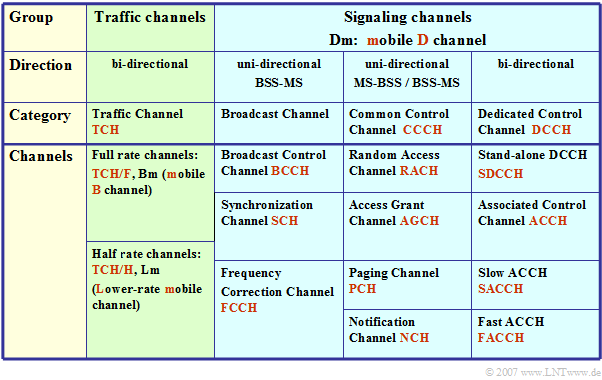
Compilation of the logical channels of GSM

Let's start with the »logical channels«. These can occupy either an entire physical channel or only a portion of a physical channel and fall into two categories:

»Traffic Channels« are used exclusively for the transmission of user data streams such as voice, fax and data. These channels are for both directions

mobile station $\rm (MS)$ ⇔ base station subsystem $\rm (BSS)$

designed and can be occupied either by a full rate traffic channel $\text{(13 kbit/s)}$ or by two half rate channels $\text{(5.6 kbit/s)}$ each.

»Control Channels« supply all active mobile stations via the radio interface by means of packet-oriented signaling in order to be able to receive messages from the base transceiver station $\rm (BTS )$» or send messages to the BTS at any time.

The table lists the logical channels of the GSM;

These differ from the logical ISDN channels by an additional "m" for "mobile".

For example, the "Bm channel" is comparable to the "B channel" of ISDN.

Uplink and downlink parameters

The logical channels are mapped to »physical channels« which describe all physical aspects of data transport:

Frequency ranges of the standardized GSM systems

the frequency ranges for »uplink« $($radio link mobile station ⇒ base station$)$ and »downlink« $($radio link base station ⇒ mobile station$)$,

the division between »Time Division Multiple Access« $\rm (TDMA)$» and »Frequency Division Multiple Access« $\rm (FDMA)$,

the »burst structure«, i.e. the occupancy of a TDMA time slot in different applications $($user and signaling data, synchronization marks, etc.$)$,

the »modulation method« "Gaussian Minimum Shift Keying" $\rm (GMSK)$, a variant of "Continuous Phase – Frequency Shift Keying" $\text{(CP-FSK)}$ with large bandwidth efficiency.

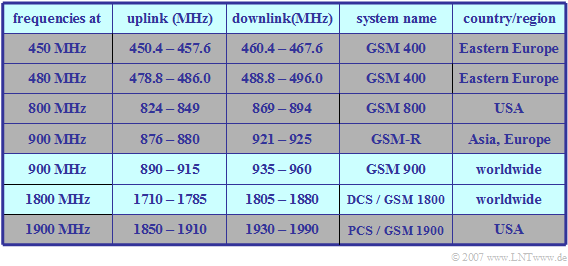
The table shows the frequency ranges of the standardized GSM systems:

To prevent intermodulation interference between the two directions, there is a "guard band" between the bands for uplink and downlink, the so-called "duplex spacing".

$\text{Example 1:}$ With system $\text{GSM 900}$ $($"D-network"$)$ the uplink starts at $\text{890 MHz}$ and the downlink at $\text{935 MHz}$.

The duplex spacing is thus $\text{45 MHz}$.

Both the uplink and the downlink have a bandwidth of $\text{25 MHz}$.

After subtracting the guard bands of $\text{100 kHz}$ at each of the two edges there remain $\text{24.8 MHz}$, which are divided into $124$ FDMA channels of $\text{200 kHz}$ each.

⇒ The $\text{DCS band}$ $($"E-network"$)$ in the range around $\text{1800 MHz}$ has a duplex spacing of $\text{95 MHz}$ and a respective bandwidth of $\text{75 MHz}$.

Taking into account the guard bands, this results in $374$ FDMA channels at $\text{200 kHz}$ each.

Realization of FDMA and TDMA

Interaction between FDMA and TDMA in GSM

In the GSM system, two multiple access methods are used in parallel:

Frequency Division Multiple Access $\rm (FDMA)$, and
Time division multiple access $\rm (TDMA)$.

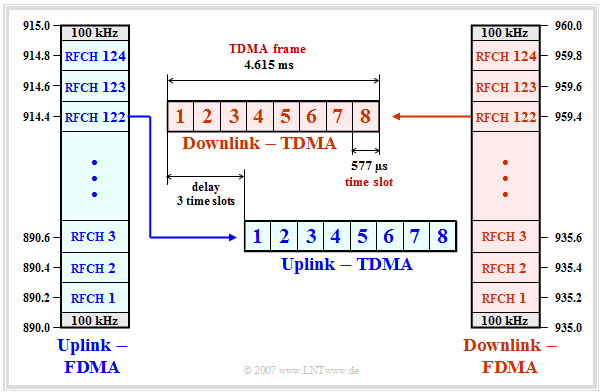
The graphic and description apply to the $\text{GSM 900}$ system. Comparable statements apply to the other GSM systems. We also refer here to the section "GSM frame structure" and "Exercise 3.3".

In both the uplink and downlink, the transmission of signaling and traffic data occurs in parallel in $124$ frequency channels, designated "RFCH1" to "RFCH124".

The center frequency of the uplink channel $n \ ( = 1$, ... , $124)$ is at

$$f_n= 890 \ {\rm MHz} + n \cdot 0.2 \ {\rm MHz}.$$

At the upper and lower ends of the $25 \ {\rm MHz}$ band, there are guard bands of $100 \ {\rm kHz}$ each.

The channel $n$ in the downlink is above the channel $n$ in the uplink by the duplex spacing of $45 \ {\rm MHz}$. The channels are designated in the same way as those in the uplink. Center frequencies:

$$f_n =935 \ {\rm MHz} + n \cdot 0.2 \ {\rm MHz}.$$

Each cell is assigned some frequencies per "cell allocation" $\rm (CA)$. In adjacent cells one uses different frequencies.

A subset of the CAs is reserved for logical channels. The remaining channels are allocated to a mobile station as "mobile allocation" $\rm (MA)$.

This is used, for example, for "frequency hopping", where the data is sent over different frequency channels. This makes the transmission more stable against channel fluctuations. In most cases, frequency hopping is performed in packets.

The individual GSM frequency channels are further subdivided by time division multiplexing $\rm (TDMA)$. Each FDMA channel is periodically divided into so-called "TDMA frames" which in turn each comprise eight time slots.

The "time slots" $($"TDMA channels"$)$ are cyclically assigned to the individual subscribers and each contain a so-called "burst" of $156.25$ bit periods in length. Each GSM user has exactly one of the eight time slots available in each TDMA frame.

The TDMA frames of the uplink are sent with three time slots delay compared to those of the downlink. This has the advantage that the same hardware of a mobile station can be used for both sending and receiving a message.

The duration of a "time slot" $($German: "Zeitschlitz" ⇒ subscript "Z"$)$ is $T_{\rm Z} ≈ 577 \rm µ s$, that of a TDMA frame $4.615 \rm ms$. These values result from the GSM frame structure. In total $26$ TDMA frames are combined into a so-called "multiframe" of duration $120 \ \rm ms$:

$$T_{\rm Z} = \frac{120\,{\rm ms}}{8 \cdot 26} \approx 576.9\,{\rm µ s }\hspace{0.05cm}. $$

The different burst types in GSM

The different burst types with GSM

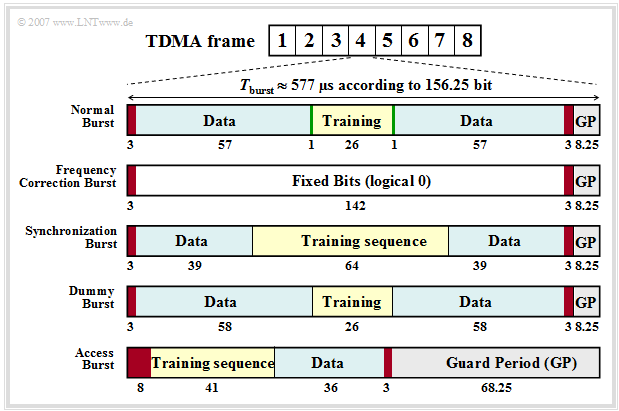
As just shown, a »burst« contains $156.25$ bits each and has duration

$$T_{\rm burst} = T_{\rm Z} ≈ 577 \rm µ s.$$

From this, the bit duration is calculated to

$$T_{\rm B} ≈ \frac{T_{\rm burst} }{156.25} \approx3.69 \rm µ s.$$

To avoid overlapping of bursts due to different propagation times between mobile and base station, a »Guard Period« $\rm (GP)$» is inserted at the end of each burst. This guard period is $8.25$ bit durations, so

$$T_{\rm GP}= 8.25 \cdot \cdot T_{\rm B} = 8.25 \cdot 3.69 \ {\rm µ s} \approx 30.5 \ {\rm µ s}.$$

⇒ There are five different types of bursts, as shown in the figure on the right:

Normal Burst $\rm (NB)$,
Frequency Correction Burst $\rm (FB)$,
Synchronization Burst $\rm (SB)$,
Dummy Burst $\rm (DB)$,
Access Burst $\rm (AB)$.

(1) The »Normal Burst« is used to transmit data from traffic and signaling channels. The error protection encoded user data $($blue, two times $57$ bits$)$ together with three tail bits each $($red, during this time the transmitted power is regulated$)$, two signaling bits $($green) and $26$ bits for the training sequence $($yellow, required for channel estimation and synchronization$)$ result in a total of $148$ bits. Added to this is the Guard Period of $8.25$ bits $($gray$)$.

The two $($green$)$ signaling bits – also called "stealing flags" – indicate whether the burst transports only user data or high-priority signaling information, which is always to be transmitted without delay. The "training sequence" is used to estimate the channel, which is a prerequisite for applying an equalizer to reduce intersymbol interference.

(2) The »Frequency Correction Burst« is used to frequency synchronize a mobile station. All bits except the tail bits and the guard period are here set to logical "$0$". The repeated broadcast of such a burst on the "frequency correction channel" $\rm (FCCH)$ corresponds to an unmodulated carrier signal with frequency $f_{\rm T} + Δf_{\rm A}$ $($carrier frequency + frequency deviation$)$. This value results from the fact that the modulation method $\text{Gaussian Minimum Shift Keying}$ is a FSK special case.

(3) The »Synchronization Burst« is used to transmit information that helps a mobile station synchronize in time with the base transceiver station. Besides a long midamble of $64$ bits, the synchronization burst contains the TDMA frame number and the "base transceiver station identity code" $\rm (BSIC)$. When such a burst is repeatedly broadcast, it is referred to as the "synchronization channel" $\rm (SCH)$.

(4) The »Dummy Burst« is transmitted by each base transceiver station $\rm (BTS)$ on a frequency specially allocated to it $($"cell allocation"$)$ when there are no other bursts to be transmitted. This ensures that a mobile station can always take power measurements.

(5) The »Access Burst« is used for random multiple access on the "random access channel" $\rm (RACH)$. To keep the probability of collisions on the RACH low, the "access burst" has a substantially longer "guard period" of $68.25$ bit durations than the other bursts.

GSM frame structure

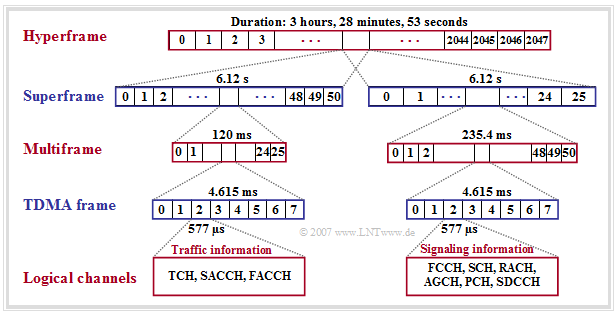
The GSM frame structure

The GSM frame structure is used to map logical channels to physical channels. Here a distinction is made between

the »mapping in frequency«, based on

"cell allocation" $\rm (CA)$,
"mobile allocation" $\rm (MA)$,
the "TDMA frame number" $\rm (FN)$, and
the rules for the $($optional$)$ "frequency hopping";

the »mapping in time«, where the TDMA frames are grouped into

multiframes,
superframes, and
hyperframes,

each with eight time slots for transmitting the bursts.

⇒ According to this graphic, the following statements are valid:

(1) »Multiframes« are used for mapping logical channels to physical channels. Two types can be distinguished here,

those with $26$ TDMA frames and a cycle duration of $120 \ \rm ms$, and

those with $51$ TDMA frames and a duration of $235.4 \ \rm ms$.

⇒ The bursts of the traffic channels $\rm (TCH)$ and the associated control channels $\rm (SACCH, FACCH)$ are transmitted in $26$ successive TDMA frames each. Only one time slot per TDMA frame is always considered for the respective multiframe.

⇒ Of the gross data rate $\text{(approx. 33.9 kbit/s)}$ per user are $\text{9.2 kbit/s}$ reserved for synchronization, signaling and guard period and $\text{1.9 kbit/s}$ for $\rm SACCH$ and $\rm IDLE$. The $($encoded and encrypted$)$ user data occupy here only $\text{22.8 kbit/s}$.

⇒ The multiframe structure with $51$ frames $($right half of the graph$)$ is used to multiplex several logical channels onto one physical channel. In $51$ consecutive TDMA frames, all data of the signaling channels $($except $\rm FACCH$ and $\rm SACCH)$ are transmitted respectively.

(2) One »superframe« consists of $1326$ consecutive TDMA frames $(51$ multiframes with each $26$ TDMA frame or $26$ multiframes with each $51$ TDMA frame$)$ and lasts approximately $T_{\rm superframe}=6.12$ seconds.

(3) A »hyperframe« groups $2048$ superframes $(2\hspace{0.08cm}715{\hspace0.08cm}648$ TDMA frames$)$ together and is used with its long cycle duration to synchronize the payload encryption. This is:

$$T_{\rm hyperframe}=\text{3 hours, 28 minutes and 53.760 seconds}.$$

Modulation in GSM systems

According to the statements of the last sections, $156.25$ bits per time slot $(0.5769 \ \rm ms)$ must be transmitted in one frequency channel.

This corresponds to a total bit rate $($for eight TDMA users including channel coding, signaling and synchronization information, etc.$)$ of $R_{\rm total} = 270\hspace{0.08cm}833 \rm bit/s$.
For this bit rate, a bandwidth of $B = 200 \ \rm kHz$ is available for GSM ⇒ required is a modulation method with a bandwidth efficiency of at least $β =R_{\rm ges}/B = 1.35$.
In GSM mobile radio, the modulation method »Gaussian Minimum Shift Keying« $\rm (GMSK)$ is used.

Here follows a brief, bullet-point description:

GMSK is a modified form of "Frequency Shift Keying" $\rm (FSK)$. This results from driving a $\text{Frequency Modulator}$ with a binary bipolar rectangular input signal.

Such an FSK signal $s(t)$ contains within each symbol duration $T$ only a single instantaneous frequency at a time; $f_{\rm A}(t) = \rm const. $

If the $($normalized$)$ input signal is equal $+1$, then $f_{\rm A}(t)$ is equal to the sum of the carrier frequency $f_{\rm T}$ and the frequency deviation $Δf_{\rm A}$.

Correspondingly, for the normalized input signal $-1$: $f_{\rm A}(t) = f_{\rm T} - Δf_{\rm A}$.

To allow easy demodulation, the two signals with frequencies $f_{\rm T} ± Δf$ should be orthogonal to each other within the symbol duration $T$. Consequently:

$$\int^{T} _{0} \cos \big(2 \pi t \cdot (f_{\rm T}+ \Delta f_{\rm A} )\big)\cdot \cos \big(2 \pi t \cdot (f_{\rm T}- \Delta f_{\rm A} )\big)\,{\rm d}t= 0\hspace{0.05cm}. $$

This results in the requirement for the "frequency deviation":

$$\Delta f_{\rm A} = \frac{k}{4 \cdot T}\hspace{0.4cm}{\rm with}\hspace{0.4cm}k = 1,\ 2,\ 3,\ \text{...}$$

In FSK systems the "modulation index" is defined to $h = 2 \cdot Δf_{\rm A} \cdot T$, it follows $h = k/2$.

Thus, the smallest modulation index under compliance with the orthogonality conditions is $h_{\rm mim} = 0.5$.

An FSK system with $h = 0.5$ ⇒ $Δf_{\rm A}$ = ${1}/{4T}$ is called $\text{Minimum Shift Keying}$ $\rm (MSK)$.

This is used in all GSM systems, because a larger modulation index than $h = 0.5$ would require a significantly larger bandwidth.

A very narrow spectrum results, if phase jumps are avoided at the symbol boundaries by phase matching ⇒ MSK belongs to the "continuous phase FSK" techniques.

An additional low-pass filter with Gaussian characteristics is inserted before the frequency modulator ⇒ further reducing the GSM bandwidth.

This modulation type is called $\text{Gaussian Minimum Shift Keying}$ $\rm (GMSK)$.

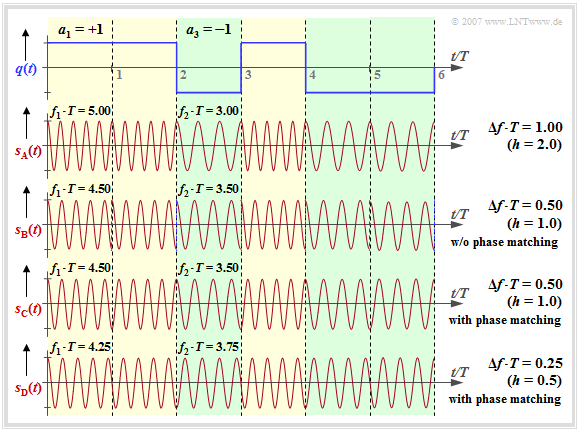
Continuous phase adjustment with FSK

Starting from the rectangular wave signal $q(t)$ and the carrier frequency $f_{\rm T} = 4/T$ we consider the FSK signals $s_{\rm A}(t)$, ... , $s_{\rm D}(t)$ at different frequency deviation $Δf_{\rm A}$ ⇒ modulation index $h = 2 \cdot Δf_{\rm A} \cdot T$.

Example signals for continuous phase adjustment

Regarding the signal characteristics shown on the right, it is to be noted $($we also refer to the $($German language$)$ SWF applet "Frequency Shift Keying & Continuous Phase Modulation"):

The signal $s_{\rm A}(t)$ results in $Δf_{\rm A} = 1/T$ ⇒ modulation index $h = 2$. One can see the higher frequency $f_1 = 5/T$ $($for $a_ν = +1)$ compared to the frequency $f_2 = 3/T$ $($for $a_ν = -1)$.
With $Δf_{\rm A} = 0.5/T$ $($signal $s_{\rm {\rm B}}(t)$, $h = 1)$ holds $f_1 = 4.5/T$ and $f_2 = 3.5/T$. At each symbol boundary, a phase jump of $π$ occurs if no phase adjustment is made as for the signal $s_{\rm C}(t)$.
When $s_{\rm C}(t)$ is applied in the range $0$ ... $T$ the coefficient $a_1 = +1$ is represented by $\cos(2π-f_1-t)$ while $a_2 = +1$ in the range $T$ ... $2T$ leads to the signal $-\cos(2π-f_1\hspace{0.01cm}-\hspace{0.01cm}(t-T))$. Phase jumps are thus avoided by this adjustment.
The signal $s_{\rm D}(t)$ describes the MSK signal $($frequency deviation $Δf_{\rm A} = 0.25/T$ ⇒ modulation index $h = 0.5)$ with phase adjustment. Here, at each symbol boundary four different initial phases are possible – depending on the previous symbols.
For the $\rm GSM \ 900$ system the carrier frequency is $f_{\rm T} = 900\ \rm MHz$ and the symbol duration is $T ≈ 3.7 \ \rm µ s$. With the modulation index $h = 0.5$ ⇒ $Δf_{\rm A} ≈ 68 \ \rm kHz$. Thus, the two frequencies are very close to each other: $f_1 = 900.068\ \rm MHz$, $f_2 = 899.932\ \rm MHz$.

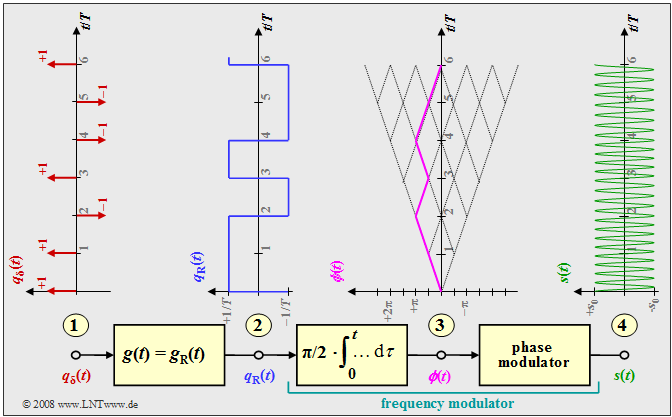
Minimum Shift Keying (MSK)

The diagram shows the model for generating an MSK modulation and typical signal characteristics. One recognizes:

Block diagram for generating an MSK and corresponding signal characteristics

At point (1) the digital source signal consisting of a sequence of Dirac delta pulses at distance $T$ weighted by the amplitude coefficients $a_ν ∈ \{-1, +1\}$:

$$q_\delta(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot \delta (t - \nu \cdot T)\hspace{0.05cm}; $$

at point (2): the rectangular source signal $q_{\rm R}(t)$ after convolution with the rectangular pulse $g(t)$ the duration $T$ and the height $1/T$ $($the amplitude was chosen this way for compatibility with later sections$)$:

$$q_{\rm R}(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (t - \nu \cdot T)\hspace{0.05cm}; $$

at point (3): the frequency modulator, which can be realized according to the description in chapter "Signal characteristics in FM" as an integrator followed by a phase modulator. For the signal at point (3) holds:

$$\phi(t) = \frac{\pi}{2}\cdot \int_{0}^{t} q_{\rm R}(\tau)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$

The phase values at $\nu \cdot T$ are multiples of $π/2 \ (90^\circ)$, taking into account the modulation index $h = 0.5$ valid for MSK. The phase response is linear.

From this, at the point (4) of the block diagram, the MSK signal is given by

$$s(t) = s_0 \cdot \cos \big(2 \pi f_{\rm T} \hspace{0.05cm}t + \phi(t)\big) = s_0 \cdot \cos \big(2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} )\big) \hspace{0.05cm}.$$

Note:

The realization of "Minimum Shift Keying" $\rm (MSK)$ by a special variant of "Offset-QPSK" is illustrated by the (German language) SWF applet "QPSK and Offset-QPSK".

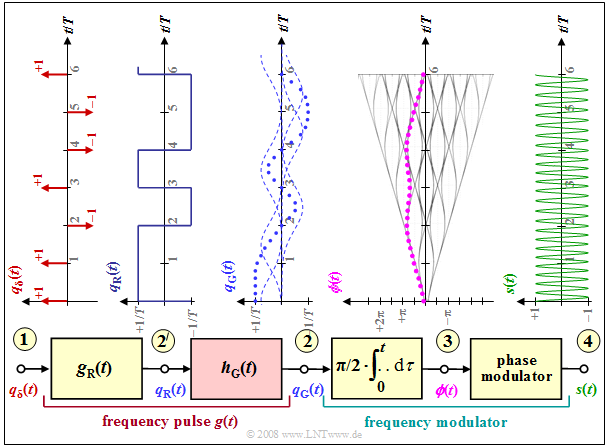
Gaussian Minimum Shift Keying (GMSK)

One advantage of MSK over other modulation types is the lower bandwidth requirement. Minor modifications to the $\text{Gaussian Minimum Shift Keying}$ - $\rm (GMSK)$ result in a narrower spectrum.

One can see from the block diagram the following differences to "Minimum Shift Keying" $\rm (MSK)$:

Block diagram for generating a GMSK and corresponding signal characteristics

The frequency pulse $g(t)$ is now no longer rectangular like the pulse $g_{\rm R}(t)$, but has flatter edges.

Consequently, there is also a smoother phase progression at point (3) than with the MSK method $($see last section$)$, where $ϕ(t)$ symbolically rises or falls linearly.

These smoother phase transitions in GMSK are achieved by a »Gaussian low-pass filter«

with "frequency response"

$$H_{\rm G}(f) = {\rm e}^{-\pi \hspace{0.05cm} \cdot \hspace{0.05cm} \big({f}/(2 \hspace{0.05cm} \cdot \hspace{0.05cm} f_{\rm G})\big)^2}$$

and "impulse response"

$$ h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\hspace{0.05cm} \cdot \hspace{0.05cm} (2 \hspace{0.05cm} \cdot \hspace{0.05cm} f_{\rm G}\hspace{0.05cm} \cdot \hspace{0.05cm} t)^2}\hspace{0.05cm}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, H_{\rm G}(f)\hspace{0.2cm}.$$

For GSM, the 3dB cutoff frequency is set to $f_{\rm 3dB} = 0.3/T$. Thus, as shown in "Exercise 3.4", the system theoretic cutoff frequency:

$$f_{\rm G} ≈ 1.5 - f_{\rm 3dB} = 0.45/T.$$

The resulting frequency impulse $g(t)$ at point (2)' of the block diagram results from the convolution of the rectangular pulse $g_{\rm R}(t)$ with the impulse response $h_{\rm G}(t)$ of the Gaussian low-pass:

$$g(t) = g_{\rm R}(t) \star h_{\rm G}(t)\hspace{0.05cm}. $$

The GMSK-modulated signal $s(t)$ now no longer exhibits a constant frequency section by section $($per symbol duration$)$. However, it is difficult to see this difference from MSK from the signal waveform at point (4) of the block diagram.

Note: We refer here to the (German language) SWF applet "Frequency Shift Keying & Continuous Phase Modulation".

Advantages and disadvantages of GMSK

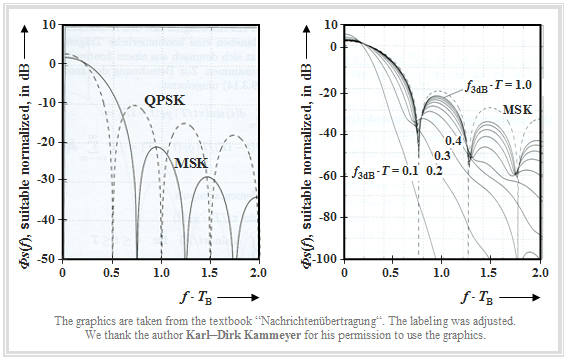
Here, the main features of the modulation method "Gaussian Minimum Shift Keying" are summarized. The following graphic was taken from the book [Kam04]^[1] .

Power-spectral densities of QPSK and MSK

⇒ The left graph shows the log power-spectral density $10 \cdot \text{lg} \ {\it Φ}_s(f)/{\it Φ}_0$ of "Minimum Shift Keying" $\rm (MSK)$ compared to "Quaternary Phase Shift Keying" $\rm (QPSK)$, where ${\it Φ}_0$ was chosen "suitable".

On the abscissa is plotted the normalized frequency $f \cdot T_{\rm B}$. For MSK, the bit duration $T_{\rm B}$ is equal to the symbol duration $T$, while for QPSK holds: $T_{\rm B} = T/2$.

One recognizes from this left representation:

The first zero in the power-spectral density $\rm (PSD)$ occurs at the normalized abscissa value $f \cdot T_{\rm B} = 0.5$ for QPSK $($dashed curve$)$, but for MSK only at $f\cdot T_{\rm B} = 0.75$.
In the further course, however, MSK results in a much faster PSD decay than the asymptotic $f^{-2}$ decay for QPSK.
Note that for MSK a cosine pulse is used for spectral shaping and for QPSK a rectangular pulse.

⇒ The right plot shows the influence of Gaussian pulse shaping in GMSK on the power-spectral density ${\it Φ}_s(f)$, where the normalized 3dB cutoff frequency is used as parameter.

In this diagram, which refers exclusively to $\rm (G)MSK$, the abscissa could also be labeled $f \cdot T$.

The smaller $f_{\rm 3\ dB}$ is, the more narrowband is the power-spectral density. In the GSM standard $f_{\rm 3\ dB} \cdot T$ = 0.3 has been specified. With this value, the bandwidth is already decisively reduced, resulting in lower interferences for adjacent channels.
On the other hand, with this cutoff frequency "intersymbol interferences" already have a serious effect. The eye opening is smaller than $50\%$ and a suitable equalization has to be provided.

$\text{Conclusions:}$ The main advantage of GMSK is its very low bandwidth requirements.

Furthermore, it should be noted:

Binary FSK – even with continuous phase matching – generally represents a nonlinear modulation process. Therefore, coherent demodulation is actually not possible.

An exception is the MSK as a special case for the modulation index $h = 0.5$, which can be realized linearly as "Offset-QPSK" and thus can also be demodulated coherently.

Without taking intersymbol interference into account, the »bit error probability« is as follows:

$$p_{\rm B} = {\rm Q} \left(\sqrt{ {E_{\rm B} }/{N_0} }\hspace{0.09cm}\right) = {1}/{2}\cdot{\rm erfc} \left(\sqrt{ {E_{\rm B} }/{2N_0} }\hspace{0.09cm}\right) \hspace{0.05cm}.$$

⇒ Compared to the QPSK, there is a degradation of $3\ \rm dB$. Note: The HTML5/JavaScript applet "Complementary Gaussian Error Functions" provides the numerical values of the functions ${\rm Q}(x)$ resp. $1/2 \cdot {\rm erfc}(x)$ used here.

An advantage of GMSK over QPSK is that a constant envelope is obtained despite the spectral shaping of the basic pulse $g(t)$. Therefore, nonlinearities on the channel do not play as large a role as in other modulation schemes. This allows the use of simple and inexpensive power amplifiers, lower power consumption and thus also longer operating times of battery-powered devices.

Radio Subsystem Link Control

Another function of the radio interface is the control of the radio link. Thus, the so-called "Radio Subsystem Link Control" performs the following tasks:

It is responsible for the measurement of the reception quality. During an established traffic or signaling connection, the channel measurement of the mobile station is performed at regular intervals with regard to received field strength and bit error rate ⇒ »Quality Monitoring«. These values are transmitted in a measurement report to the base station via the signaling channel SACCH and used by it for power control and handover.
The "Power Control" is necessary to ensure that all mobile stations only radiate with the minimum required power. The transmitted power can be adaptively controlled in steps of $2 \ \rm dBm$ between $43 \ \rm dBm$ $\text{(level 0:}$ $20\ \rm W)$ and $13 \ \rm dBm$ $\text{(level 15:}$ $20\ \rm mW)$.
Base station transmitted power is also adjusted in steps of $2 \rm dBm$ to achieve optimum network capacity. An exception is the BCCH carrier with constant transmitted power to allow mobile stations to make comparative measurements of neighboring BCCH carriers.
The »Adaptive Frame Alignment« – i.e. adaptive frame synchronization – is used to avoid collisions between uplink and downlink data to be transmitted or received by the mobile station offset by three time slots.

Adaptive Frame Alignment

This is shown in the adjacent graph. The downlink is represented in the middle area with a yellow background, where the data arrives at the mobile station $\rm (MS)$ by the time $T_{\rm R}$ $($"Round Trip Delay Time", by the time $T_{\rm R}$ $($"Round Trip Delay Time", green marking$)$ later than it was sent by the base transceiver station $\rm (BTS)$.

In the upper area, the uplink is shown without "Timing Advance".

The MS starts sending exactly three time slots after reception $($blue marker$)$.
Due to the delays in downlink and uplink, the time slot "$0$" does not reach the BTS at the time $3T_{\rm burst}$ as required, but by $2T_{\rm R}$ later $($red mark$)$.
With the "Timing Advance" uplink $($lower sketch$)$ this delay is already compensated by the mobile station by sending the data by the time $ 2T_{\rm R}$ earlier and thus they arrive exactly time synchronized at the BTS.

The stages $0 - 63$ are available for "Timing Advance", where each stage corresponds to one bit duration $T_{\rm B}$.

The maximum timing advance is thus $\rm 63 \cdot 3.7 \ µ s ≈ 233 \ µs$, giving the maximum allowable runtime in one direction to $T_{\rm R} ≈ 116\ {\rm µ s}$.
From this, the allowed cell radius of GSM $($distance between BTS and MS$)$ can be calculated:

$$116\ \rm µ s · 3 · 10^8 \ m/s ≈ 35 \ km.$$

Exercises for the chapter

Exercise 3.3: GSM Frame Structure

Exercise 3.3Z: GSM 900 and GSM 1800

Exercise 3.4: GMSK Modulation

Exercise 3.4Z: Continuous Phase Frequency Shift Keying

References

↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4th edition, 2004.

[Kam04-1] Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4th edition, 2004.

[1]