Aufgaben:Exercise 3.6: Adaptive Multi Rate Codec

• Return to book

Tracks of the AMR codec

In the late 1990s, a very flexible, adaptive speech codec was developed and standardised in the form of the AMR codec. This provides a total of eight different modes with data rates between  $4.75 \ \rm kbit/s$  and  $12.2 \ \rm kbit/s$ .

The AMR codec, like the full rate codec (FRC) discussed in  "Exercise 3.5" , includes both a short-term prediction (LPC) and a long-term prediction (LTP). However, these two components are realised differently from FRC.

The main difference between AMR and FRC is the coding of the residual signal (after LPC and LTP):

• Instead of "Regular Pulse Excitation" (RPE), the "Algebraic Code Excitation Linear Prediction" (ACELP) procedure is used for the AMR code.
• From the fixed codebook (FCB), for each subframe of  $5 \ \rm ms$  duration, the FCB pulse and FCB gain that best match the residual signal (for which the mean square error of the difference signal becomes minimum) is selected.

Each entry in the fixed codebook identifies a pulse where exactly  $10$  of  $40$  positions are occupied by  $\pm1$ . In this regard it should be noted:

• The pulse is divided into five tracks with eight possible positions each, where track  $1$  contains the positions  $1,\ 6,\ 11$, ... , $36$  of the subframe and track  $5$  the positions  $5,\ 10,\ 15$, ... , $40$  describes.
• In each track there are exactly two values  $\pm1$, while all the other six values are  $0$ . The two  $±1$-positions are each assigned three bits - i.e. with  $000$, ... ,  $111$ - are coded.
• Another bit is used for the sign of the first-mentioned pulse, where a "$1$" indicates a positive sign and a "$0$" a negative sign.
• If the pulse position of the second pulse is greater than that of the first pulse, the second pulse has the same sign as the first, otherwise the opposite.
• Thus, seven bits per track are transmitted to the receiver, plus five bits for the so-called FCB amplification.

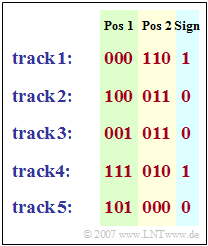
In the diagram, the  $35$  bits describing an FCB pulse are given as an example.

Track 1 includes.

• a positive pulse  $({\rm VZ} = 1)$  at  $1$  (first possible position for track 1)  $\hspace{0.2cm}\text{plus}\hspace{0.2cm}0$ (bit specification for " 000") $= 1$,
• another positive pulse (since $110 > 000$) at position $1 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5$ (pulse spacing in each track) $\hspace{0.2cm}\text{mal}\hspace{0.2cm}6$ (bit specification for " 110") = $31\hspace{0.05cm}.$

Track 2 includes.

• a negative pulse (${\rm VZ} = 0$) at $2$ (first possible position for track 2) $\hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{mal}\hspace{0.2cm}4$ (bit specification for " 100") = $22\hspace{0.05cm},$
• a positive pulse (sign reversal due to $011 > 100$) at position $2 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{mal}\hspace{0.2cm}3$ (bit specification for " 011") = $17\hspace{0.05cm}.$

Hint:

• This exercise belongs to the chapter  "Speech Coding".

• When entering the pulse positions  $N_{1}$  denotes the first triple of bits and  $N_{2}$  the second.
• For example, for track  $2$  one would have to enter the values  $N_{1}=-22$  and  $N_{2}=+17$ .

Questions

1

How many bits describe a speech frame $($of duration  $20 \ \rm ms)$  in  $12.2 \ \rm kbit/s$ mode?

$N_{12.2} \ = \ $ $ \ \rm Bit$

2

How many bits are needed for FCB pulse and gain per frame?

$N_{\rm FCB} \ = \ $ $ \ \rm Bit$

3

How many bits are left for LPC and LTP?

$N_{\rm LPC/LTP} \ = \ $ $ \ \rm Bit$

4

What subframe pulse positions and signs does track  $3$ describe?
Follow the instructions for input on the input page.

$N_{1} \ = \ $

$N_{2} \ = \ $

5

What pulse positions including sign describe the track  $4$?

$N_{1} \ = \ $

$N_{2} \ = \ $

6

What pulse positions including sign describe the track  $5$?

$N_{1} \ = \ $

$N_{2} \ = \ $

Solution

Solution

(1)  With the data rate $12.2 \ \rm kbit/s$, exactly $\underline{244 \ \rm bit}$ results within $20 \ \rm ms$, while for example in $4.75 \ \rm kbit/s$ mode only $95 \ \rm bit$ is transmitted.

(2)  In each subframe, the FCB pulse requires $35 \ \rm bit$ (five tracks of seven bits each) and the FCB gain requires five bits.

• With four subframes, this gives $N_{\rm FCB} \underline{= 160 \ \rm bits}$.

(3)  This leaves the difference from (1) and (2), i.e. $N_{\rm LPC/LTP}\underline{ = 84 \rm bits}$.

(4)  The sign bit "$0$" indicates a negative first pulse.

• Because $001 < 011$, the second pulse has the same sign.
• The two amounts result in

$$|N_1| \ = \ 3 \hspace{0.1cm}{\rm(da \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 1 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 001)} = 8\hspace{0.05cm}, $$

$$ |N_2| \ = \ 3 \hspace{0.1cm}{\rm(da \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 3 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 011)} = 18\hspace{0.05cm}.$$

• Therefore, to be entered for the third track is $N_{1} \underline{ = -8}$ and $N_{2} \underline{ = -18}.$

(5)  In an analogous way, for track $4$ we obtain the values  $N_{1} \underline{ = +39}$  and  $N_{2} \underline{ = -14}$.

(6)  The fifth track provides  $N_{1} \underline{ =-30}$  and  $N_{2} \underline{ = +5}$