Difference between revisions of "Aufgaben:Exercise 3.6: Adaptive Multi Rate Codec"
m (Guenter moved page Exercise 3.6: Adaptive Multi–Rate Codec to Exercise 3.6: Adaptive Multi Rate Codec) |
|||
| Line 4: | Line 4: | ||
[[File:En_Bei_A_3_6.png|right|frame|Tracks of the AMR codec]] | [[File:En_Bei_A_3_6.png|right|frame|Tracks of the AMR codec]] | ||
| − | In the late 1990s, a very flexible, adaptive speech codec was developed and | + | In the late 1990s, a very flexible, adaptive speech codec was developed and standardized in the form of $\rm AMR$ codec. This provides a total of eight different modes with data rates between $4.75 \ \rm kbit/s$ and $12.2 \ \rm kbit/s$. |
| − | The AMR codec, like the full rate codec (FRC) discussed in [[Aufgaben:Exercise_3.5:_GSM_Full-Rate_Voice_Codec| | + | The AMR codec, like the full rate codec $\rm (FRC)$ discussed in [[Aufgaben:Exercise_3.5:_GSM_Full-Rate_Voice_Codec|$\text{Exercise 3.5}$]], includes both a short-term prediction $\rm (LPC)$ and a long-term prediction $\rm (LTP)$. However, these two components are realized differently from FRC. |
| − | The main difference between AMR and FRC is the | + | The main difference between AMR and FRC is the encoding of the residual signal $($after LPC and LTP$)$: |
| − | + | #Instead of "Regular Pulse Excitation" $\rm (RPE)$, here the "Algebraic Code Excitation Linear Prediction" $\rm (ACELP)$ is used. | |
| − | + | #From the fixed code book $\rm (FCB)$, for each subframe of $5 \ \rm ms$ duration, the "FCB pulse" and the "FCB gain" that best match the residual signal $($for which the mean square error of the difference signal becomes minimum$)$ is selected. | |
| − | Each entry in the fixed | + | Each entry in the fixed code book identifies a pulse where exactly $10$ of $40$ positions are occupied by $\pm1$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In this regard it should be noted: | ||
| + | *The pulse is divided into five tracks with eight possible positions each, where track $1$ contains the positions $1,\ 6,\ 11$, ... , $36$ of the subframe and track $5$ describes the positions $5,\ 10,\ 15$, ... , $40$. | ||
| − | In the diagram, the $35$ bits describing an FCB pulse are given as an example | + | *In each track there are exactly two values $\pm1$, while all the other six values are zero. |
| + | |||
| + | *The two $±1$-positions are each assigned three bits – i.e. encoded with "$000$", ... , "$111$". | ||
| + | |||
| + | *Another bit is used for the "sign of the first-mentioned pulse", where a "$1$" indicates a positive sign and a "$0$" a negative sign. | ||
| + | |||
| + | *If the pulse position of the second pulse is greater than that of the first pulse, the second pulse has the same sign as the first, otherwise the opposite. | ||
| + | |||
| + | *Thus, seven bits per track are transmitted to the receiver, plus five bits for the so-called "FCB amplification''. | ||
| + | |||
| + | |||
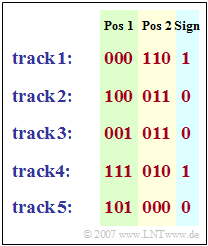
| + | In the diagram, the $35$ bits describing an FCB pulse are given as an example: | ||
| − | '''Track 1''' includes | + | ⇒ '''Track 1''' includes |
| − | + | #a positive pulse $({\rm sign} = 1)$ at position $\big [1$ (first possible position for track 1) $\hspace{0.02cm}\text{plus}\hspace{0.2cm}0$ (bit specification for "000") $= 1\big]$, | |
| − | + | #another positive pulse $($since $110 > 000)$ at position $\big [1 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5$ (pulse spacing in each track) $\hspace{0.2cm}\text{mal}\hspace{0.2cm}6$ (bit specification for " 110") = $31\hspace{0.05cm}.$ | |
Revision as of 12:56, 25 January 2023
In the late 1990s, a very flexible, adaptive speech codec was developed and standardized in the form of $\rm AMR$ codec. This provides a total of eight different modes with data rates between $4.75 \ \rm kbit/s$ and $12.2 \ \rm kbit/s$.
The AMR codec, like the full rate codec $\rm (FRC)$ discussed in $\text{Exercise 3.5}$, includes both a short-term prediction $\rm (LPC)$ and a long-term prediction $\rm (LTP)$. However, these two components are realized differently from FRC.
The main difference between AMR and FRC is the encoding of the residual signal $($after LPC and LTP$)$:
- Instead of "Regular Pulse Excitation" $\rm (RPE)$, here the "Algebraic Code Excitation Linear Prediction" $\rm (ACELP)$ is used.
- From the fixed code book $\rm (FCB)$, for each subframe of $5 \ \rm ms$ duration, the "FCB pulse" and the "FCB gain" that best match the residual signal $($for which the mean square error of the difference signal becomes minimum$)$ is selected.
Each entry in the fixed code book identifies a pulse where exactly $10$ of $40$ positions are occupied by $\pm1$.
In this regard it should be noted:
- The pulse is divided into five tracks with eight possible positions each, where track $1$ contains the positions $1,\ 6,\ 11$, ... , $36$ of the subframe and track $5$ describes the positions $5,\ 10,\ 15$, ... , $40$.
- In each track there are exactly two values $\pm1$, while all the other six values are zero.
- The two $±1$-positions are each assigned three bits – i.e. encoded with "$000$", ... , "$111$".
- Another bit is used for the "sign of the first-mentioned pulse", where a "$1$" indicates a positive sign and a "$0$" a negative sign.
- If the pulse position of the second pulse is greater than that of the first pulse, the second pulse has the same sign as the first, otherwise the opposite.
- Thus, seven bits per track are transmitted to the receiver, plus five bits for the so-called "FCB amplification.
In the diagram, the $35$ bits describing an FCB pulse are given as an example:
⇒ Track 1 includes
- a positive pulse $({\rm sign} = 1)$ at position $\big [1$ (first possible position for track 1) $\hspace{0.02cm}\text{plus}\hspace{0.2cm}0$ (bit specification for "000") $= 1\big]$,
- another positive pulse $($since $110 > 000)$ at position $\big [1 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5$ (pulse spacing in each track) $\hspace{0.2cm}\text{mal}\hspace{0.2cm}6$ (bit specification for " 110") = $31\hspace{0.05cm}.$
Track 2 includes.
- a negative pulse (${\rm VZ} = 0$) at $2$ (first possible position for track 2) $\hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{mal}\hspace{0.2cm}4$ (bit specification for " 100") = $22\hspace{0.05cm},$
- a positive pulse (sign reversal due to $011 > 100$) at position $2 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{mal}\hspace{0.2cm}3$ (bit specification for " 011") = $17\hspace{0.05cm}.$
Hint:
- This exercise belongs to the chapter "Speech Coding".
- When entering the pulse positions $N_{1}$ denotes the first triple of bits and $N_{2}$ the second.
- For example, for track $2$ one would have to enter the values $N_{1}=-22$ and $N_{2}=+17$ .
Questions
Solution
(1) With the data rate $12.2 \ \rm kbit/s$, exactly $\underline{244 \ \rm bit}$ results within $20 \ \rm ms$, while for example in $4.75 \ \rm kbit/s$ mode only $95 \ \rm bit$ is transmitted.
(2) In each subframe, the FCB pulse requires $35 \ \rm bit$ (five tracks of seven bits each) and the FCB gain requires five bits.
- With four subframes, this gives $N_{\rm FCB} \underline{= 160 \ \rm bits}$.
(3) This leaves the difference from (1) and (2), i.e. $N_{\rm LPC/LTP}\underline{ = 84 \rm bits}$.
(4) The sign bit "$0$" indicates a negative first pulse.
- Because $001 < 011$, the second pulse has the same sign.
- The two amounts result in
- $$|N_1| \ = \ 3 \hspace{0.1cm}{\rm(da \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 1 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 001)} = 8\hspace{0.05cm}, $$
- $$ |N_2| \ = \ 3 \hspace{0.1cm}{\rm(da \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 3 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 011)} = 18\hspace{0.05cm}.$$
- Therefore, to be entered for the third track is $N_{1} \underline{ = -8}$ and $N_{2} \underline{ = -18}.$
(5) In an analogous way, for track $4$ we obtain the values $N_{1} \underline{ = +39}$ and $N_{2} \underline{ = -14}$.
(6) The fifth track provides $N_{1} \underline{ =-30}$ and $N_{2} \underline{ = +5}$