Difference between revisions of "Mobile Communications/Statistical Bindings within the Rayleigh Process"
| (93 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Time variant transmission channels |
| − | |Vorherige Seite= | + | |Vorherige Seite=Probability Density of Rayleigh Fading |
| − | |Nächste Seite= | + | |Nächste Seite=Non-Frequency Selective Fading With Direct Component |
}} | }} | ||
| − | == | + | == Some general remarks on ACF and PSD == |
<br> | <br> | ||
| − | + | The correlation between $r(t)$ and $r(t+ \Delta t)$ ⇒ [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Auto-correlation_function_for_stationary_and_ergodic_processes|$\text{auto-correlation function}$]] $\rm (ACF)$ is suitable for describing the inner statistical dependencies between the neighboring signal values: | |
| − | :<math>\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\ | + | ::<math>\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\big [ r(t) \cdot r^{\star}(t + {\rm \Delta}t)\big ] |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Compared to the definition under the link above, the following differences can be seen: | |
| − | * | + | *The ACF variable is here marked with $\Delta t$ instead of $\tau$ because in this book we need $\tau$ still for the 2D impulse response $h(t, \hspace{0.05cm}\tau)$ .<br> |
| − | * | + | *The equivalent low-pass signal $r(t)$ is complex. By the factor $1/2$ however, the ACF $\varphi_r ({\rm \Delta}t)$ and especially the power $\varphi_r ({\rm \Delta}t = 0)$ refer to the (real) band-pass signal $r_{\rm BP}(t)$.<br><br> |
| − | + | Applying the Rayleigh fading channel model ⇒ $r(t) = s(t) \cdot z(t)$ results for its ACF: | |
| − | :<math>\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\ | + | ::<math>\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\big [ s(t) \cdot z(t) \cdot s^{\star}(t + {\rm \Delta}t) \cdot z^{\star}(t + {\rm \Delta}t)\big ] = \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)\hspace{0.05cm}.</math> |
| − | + | For the ACF of the transmitted signal $s(t)$ and the multiplicative factor $z(t)$ the following definitions apply: | |
| − | :<math> \varphi_s ({\rm \Delta}t) | + | ::<math> \varphi_s ({\rm \Delta}t)= {1}/{2} \cdot {\rm E}\big [ s(t) \cdot s^{\star}(t + {\rm \Delta}t)\big ] |
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | :<math>\varphi_z ({\rm \Delta}t) | + | ::<math>\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]\hspace{0.05cm}.</math> |
| − | + | The factor $1/2$ is only to be considered for the ACF calculation of band-pass signals in the equivalent low-pass range, but not for $\varphi_z ({\rm \Delta}t)$. Otherwise $\varphi_r ({\rm \Delta}t) \ne \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)$ would result.<br> | |
| − | + | Based on the definition of $\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]$ the ACF is always real even with a complex time function $z(t)$ and also with respect to $ {\rm \Delta}t$ even. Let us further consider that | |
| − | * | + | *$z(t) = x(t) + {\rm j} \cdot y(t) $ ,<br> |
| − | * | + | *$x(t)$ and $y(t)$ have the same statistical properties, and<br> |
| − | * | + | *that no statistical dependencies exist between $x(t)$ and $y(t)$ ,<br><br> |
| − | so | + | so the ACF of the complex factor $z(t)$ can be written as: |
| − | + | ::<math>\varphi_z ({\rm \Delta}t) = \varphi_x ({\rm \Delta}t) + \varphi_y ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t) | |
| − | :<math>\varphi_z ({\rm \Delta}t) = \varphi_x ({\rm \Delta}t) + \varphi_y ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | {{BlaueBox|TEXT= | |
| − | * | + | $\text{Conclusion:}$ This results in the following simplification: |
| + | *To determine the statistical dependencies of the complex variable $z(t)$ only one of the two Gaussian processes must be considered. In the following, this is $x(t)$. | ||
| − | * | + | *We first calculate the auto-correlation function $\rm (ACF)$ $\varphi_x ({\rm \Delta}t) = {\rm E}\big[x(t) \cdot x(t + {\rm \Delta}t)\big]$ of the real part and then its power-spectral density $\rm (PSD)$ |
::<math>{\it \Phi}_x (f_{\rm D}) = \int_{-\infty}^{+\infty} \varphi_x ({\rm \Delta}t) \cdot | ::<math>{\it \Phi}_x (f_{\rm D}) = \int_{-\infty}^{+\infty} \varphi_x ({\rm \Delta}t) \cdot | ||
| − | {\rm | + | {\rm e}^{ -- {\rm j \cdot 2 \pi} \cdot f_{\rm D} \cdot {\rm \Delta}t } \hspace{0.15cm}{\rm d}( {\rm \Delta}t) |
| − | \hspace{0.3cm} \ | + | \hspace{0.3cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.3cm} \varphi_x ({\rm \Delta}t) |
| − | \hspace{0.05cm}.</math> | + | \hspace{0.05cm}. |
| + | </math> | ||
| − | * | + | *For the corresponding parameters of the complex random process $z(t)$ we have: |
::<math>\varphi_z ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t)\hspace{0.05cm},\hspace{0.2cm} | ::<math>\varphi_z ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t)\hspace{0.05cm},\hspace{0.2cm} | ||
| Line 58: | Line 58: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *The $\rm PSD$ variable is the [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#Doppler_frequency_and_its_distribution|$\text{Doppler frequency}$]] $f_{\rm D}$, because in mobile radio the so-called "Doppler effect" is the cause of the statistical dependencies. }} | |
| − | |||
| − | |||
| − | |||
| − | + | This effect is explained in the next section. | |
| − | + | == Phenomenological description of the Doppler effect== | |
| − | + | <br> | |
| + | The statistical dependencies within the real signals $x(t)$ and $y(t)$ or within the complex quantity $z(t)$ are due to the Doppler effect. This was predicted theoretically in the middle of the 19th century by the Austrian mathematician, physicist and astronomer [https://en.wikipedia.org/wiki/Christian_Doppler $\text{Christian Andreas Doppler}$] and named after him.<br> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ The »'''Doppler effect'''« refers to the change in the perceived frequency of waves of any kind that occurs when the source (transmitter) and observer (receiver) move relative to each other.}}<br> | ||
| − | + | Qualitatively, the Doppler effect can be described as follows: | |
| + | *If the observer and source approach each other, the frequency increases from the observer's point of view, regardless of whether the observer is moving or the source or both. | ||
| − | + | *If the source moves away from the observer or the observer moves away from the source, the observer perceives a lower frequency than that actually transmitted.<br><br> | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 1:}$ We look at the pitch change of the "Martinhorn" of an ambulance. As long as the vehicle approaches, the observer hears a higher tone than when the car is stationary. When the ambulance moves away, a lower tone is perceived.<br> | ||
| − | + | The same effect can be seen with a car racing note. The frequency changes and the sound are the more obvious the faster the cars are going.}}<br> | |
| − | + | In this learning tutorial you can illustrate the subject matter with the interactive applet [[Applets:The_Doppler_Effect|"The Doppler Effect"]] . | |
| − | + | [[File:P ID2113 Mob T 1 3 S2a v1.png|right|frame|Initial situation: $\rm (S)$ and $\rm (E)$ are not moving|class=fit]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ | ||
| + | Some properties of this effect, which is still known from physics lessons, will now be shown by means of snapshots of an earlier version of the above mentioned animation, where the dynamic program properties are of course lost.<br> | ||
| − | + | The first diagram shows the initial situation: | |
| + | *The stationary station $\rm (S)$ outputs the constant frequency $f_{\rm S}$ . | ||
| + | *The wave propagation is illustrated in the diagram by concentric circles around $\rm (S)$ . | ||
| + | *If the receiver $\rm (E)$ is also at rest, the frequency $f_{\rm E} = f_{\rm S}$ is then perceived.}} | ||
<br> | <br> | ||
| − | |||
| − | + | [[File:P ID2114 Mob T 1 3 S2b v2.png|right|frame|Doppler effect: $\rm (S)$ moves towards resting $\rm (E)$]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ The next snapshot shows the case where the transmitter $\rm (S)$ has moved at constant speed $v$ from its starting point $\rm (S_0)$ towards the receiver $\rm (E)$. <br> | ||
| + | *The right diagram shows that the frequency $f_{\rm E}$ (blue oscillation) perceived by the receiver is larger by about $20\%$ than the frequency $f_{\rm S}$ at the transmitter (red oscillation). | ||
| + | *Due to the movement of the transmitter, the circles are no longer concentric. | ||
| − | + | [[File:P ID2115 Mob T 1 3 S2c v2.png|left|frame|Doppler effect: $\rm (S)$ moves away from resting $\rm (E)$ ]] | |
| − | + | <br><br><br><br><br><br><br><br><br><br><br><br> | |
| − | [[File:P ID2115 Mob T 1 3 S2c v2.png| | + | * The scenario shown on the left results when the transmitter $\rm (S)$ moves away from the receiver $\rm (E)$. Then the received frequency $f_{\rm E}$ (blue oscillation) is about $20\%$ smaller than the transmitted frequency $f_{\rm S}$.<br>}} |
| − | + | <br clear=all> | |
| − | <br> | + | {{BlaueBox|TEXT= |
| − | + | $\text{However, the following must be taken into account:}$ | |
| − | + | *All these figures apply to unrealistically high speed $(v = c/5)$, where $c = 3 \cdot 10^8 \, {\rm m/s}$ indicates the speed of light. In mobile radio, the deviations between $f_{\rm S}$ and $f_{\rm E}$ are usually only a fraction of the transmission frequency. | |
| − | + | *The exact equation for the receiving frequency $f_{\rm E}$, including an angle $\alpha$ between the direction of movement and the connecting line transmitter–receiver, is | |
| − | + | ::<math>f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c \cdot \cos(\alpha)} | |
| − | |||
| − | :<math>f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c \cdot \cos(\alpha) | ||
| − | |||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | *As the [[Aufgaben:Exercise_1.4Z:_On_the_Doppler_Effect|"Exercise 1.4Z"]] will show: One can assume at realistic speeds $(v \ll c)$ the following approximation, in which the effects described by the [https://en.wikipedia.org/wiki/Theory_of_relativity $\text{Theory of Relativity}$] are disregarded: | ||
| + | ::<math>f_{\rm E} \approx f_{\rm S} \cdot \big [1 +{v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.05cm}.</math>}} | ||
| − | + | == Doppler frequency and its distribution== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | ||
<br> | <br> | ||
| − | + | We summarize the statements of the last section briefly, whereby we start from the second, i.e. the non–relativistic equation: | |
| − | * | + | *A relative movement between transmitter (source) and receiver (observer) results in a shift by the Doppler frequency $f_{\rm D} = f_{\rm E} - f_{\rm S}$. |
| − | * | + | *A positive Doppler frequency $(f_{\rm E} > f_{\rm S})$ results when transmitter and receiver move (relative) towards each other. A negative Doppler frequency $(f_{\rm E} < f_{\rm S})$ means that transmitter and receiver move away from each other (directly or at an angle).<br> |
| − | * | + | *The maximum frequency shift occurs when transmitter and receiver move directly towards each other ⇒ angle $\alpha = 0^\circ$. This maximum value depends (first approximation) on the transmission frequency $ f_{\rm S}$ and the speed $v$ $(c = 3 \cdot 10^8 \, {\rm m/s}$ indicates the speed of light$)$: |
::<math>f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.</math> | ::<math>f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.</math> | ||
| − | * | + | *If the relative movement takes place at any angle $\alpha$ to the connecting line transmitter–receiver, then the Doppler shift is |
::<math>f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) | ::<math>f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) | ||
| Line 127: | Line 129: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Conclusion:}$ Assuming equal probable directions of motion $($equal distribution for the angle $\alpha$ in the range $- \pi \le \alpha \le +\pi)$ the probability density function $($here denoted with $\rm wdf$ (from the german '''W'''ahrscheinlichkeits'''D'''ichte'''F'''unktion$)$ the Doppler frequency in the range $- f_\text{D, max} \le f_{\rm D} \le + f_\text{D, max}$: | ||
| − | :<math>{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | + | ::<math>{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Outside the range between $-f_\text{D, max}$ and $+f_\text{D, max}$ the probability density function always has the value zero.}} | |
| + | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Derivation:}$ The resulting Doppler frequency depending on the angle of movement $\alpha$ is | ||
| − | :<math>f_{\rm D} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) = g(\alpha) | + | [[File:P ID3103 Mob T 1 3 S3 v2.png|right|frame|To calculate the probability density function $\rm (PDF)$ of the Doppler frequency|class=fit]] |
| + | ::<math>f_{\rm D} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) = g(\alpha) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | We refer to this function as $g(\alpha)$ and assume that | |
| + | *$\alpha$ takes all angle values between $\pm \pi$ | ||
| + | *with equal probability ⇒ equal distribution. | ||
| + | |||
| − | :<math>{\rm wdf}(f_{\rm D})=\frac{{\rm wdf}(\alpha)}{\ | + | Then for the probability of the Doppler frequency according to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Transformation_of_random_variables|"Transformation of Random Variables"]] in the book "Stochastic Signal Theory": |
| + | |||
| + | ::<math>{\rm wdf}(f_{\rm D})=\frac{ {\rm wdf}(\alpha)}{\vert g\hspace{0.08cm}'(\alpha)\vert}\Bigg \vert_{\hspace{0.1cm} \alpha=h(f_{\rm D})} | ||
\hspace{0.05cm}</math> | \hspace{0.05cm}</math> | ||
| − | + | *with the derivative $g\hspace{0.08cm}'(\alpha)= - f_\text{D, max} \cdot \sin(\alpha)$, and | |
| + | *the inverse function $ \alpha = h(f_{\rm D})$. | ||
| − | |||
| − | = | + | In the example the inverse function is |
| − | + | :$$ \alpha = \arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}).$$ | |
| − | |||
| − | + | The diagram illustrates the calculation procedure for determining the Doppler frequency's PDF: | |
| − | * | + | *Since the characteristic curve between the Doppler frequency $f_{\rm D}$ and the angle $\alpha$ ⇒ $ g(\alpha) = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha)$ is limited by the value $f_{\rm D, \hspace{0.05cm} max}$ there is for $f_{\rm D}$ no value possible outside this range.<br> |
| − | * | + | *When transforming random variables, a distinction must be made between areas with positive and negative slopes of the transformation's characteristic curve. The $\alpha$–values between $-\pi$ and $0$ $($positive gradient of the transformation characteristic$)$ provide the result |
| − | ::<math>{\rm wdf}(f_{\rm D}) | + | ::<math>{\rm wdf}(f_{\rm D})=\frac{1/(2\pi)}{f_{\rm D, \hspace{0.05cm} max} \cdot \sin(\alpha)} \Bigg \vert_{\hspace{0.1cm} \alpha=\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})} = \frac{(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} )^{-1} }{ \sin(\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}))} = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } |
| − | |||
| − | |||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *For reasons of symmetry, the positive $\alpha$–area contributes in the same way, so that the inner total area is given by | |
| − | * | ||
::<math>{\rm wdf}(f_{\rm D}) = \frac{1}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | ::<math>{\rm wdf}(f_{\rm D}) = \frac{1}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *If $\alpha$ takes values around $\pm \pi/2$ it results in a small Doppler frequency ⇒ $f_{\rm D} \approx 0$ $($violet marking$)$. But, because of the relatively large gradient of the cosine curve $g(\alpha)$ at $\alpha = \pm \pi/2$ the PDF–value at $f_{\rm D} \approx 0$ ist very small. <br> |
| − | * | + | *Small angles $($around $\alpha \approx 0)$, however, lead to the maximum Doppler frequency ⇒ $f_{\rm D} \approx f_{\rm D, \hspace{0.05cm} max}$ $($red marker$)$. Because of the nearly horizontal characteristic curve $g(\alpha)$ here the $f_{\rm D}$–PDF is clearly larger. For $f_{\rm D} \equiv f_{\rm D, \hspace{0.05cm} max}$ this even results in an infinitely large value.<br> |
| − | * | + | *On the other hand, if $\alpha$ takes values around $\pm \pi$ it leads to the Doppler frequency $f_{\rm D} \approx -f_{\rm D, \hspace{0.05cm} max}$ $($green marker$)$. Again the characteristic curve is nearly horizontal and this results in a large PDF–value.}}<br><br> |
| − | == | + | == ACF and PSD with Rayleigh–Fading == |
<br> | <br> | ||
| − | + | We now assume an antenna with the same radiation in all directions; then the Doppler power-spectral density is identical in shape to the PDF of the Doppler frequencies. | |
| − | :<math>{\it \Phi}_z(f_{\rm D}) = | + | For ${\it \Phi}_x(f_{\rm D})$ the PDF must still be multiplied by the power $\sigma^2$ of the Gaussian process, and the resulting PSD ${\it \Phi}_z(f_{\rm D})$ of the complex factor $z(t) = x(t) + {\rm j} \cdot y(t) $ can be written after doubling as: |
| + | |||
| + | ::<math>{\it \Phi}_z(f_{\rm D}) = | ||
\left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\ | \left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| Line 185: | Line 194: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | This process is named after [http://ethw.org/William_C._Jakes,_Jr. $\text{William C. Jakes Jr.}$] the »'''Jakes spectrum'''«. The doubling is necessary, because up to now only the contribution of the real part $x(t)$ was considered. <br> | |
| − | + | The corresponding auto-correlation function $\rm (ACF)$ is obtained after a [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|$\text{inverse Fourier transformation}$]]: | |
| − | :<math>\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm},</math> | + | ::<math>\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm},</math> |
| − | + | with the Bessel function of first kind and zero order $($first equation: definition, second equation: series expansion$)$: | |
| − | :<math>{\rm J }_0 (u) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{- {\rm j }\hspace{0.03cm}\cdot \hspace{0.03cm}u \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} = \hspace{0.2cm} | + | ::<math>{\rm J }_0 (u) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{- {\rm j }\hspace{0.03cm}\cdot \hspace{0.03cm}u \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} = \hspace{0.2cm} |
\sum_{k = 0}^{\infty} \frac{(-1)^k \cdot (u/2)^{2k}}{k! \cdot \Gamma (k+1)} | \sum_{k = 0}^{\infty} \frac{(-1)^k \cdot (u/2)^{2k}}{k! \cdot \Gamma (k+1)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | [[ | + | The numerical values of this function can be obtained with the [[Applets:Bessel functions of the first kind|"applet of the same name"]]. <br> |
| + | |||
| + | [[File:P_ID2117__Mob_T_1_3_S4_v2.png|right|frame|Doppler power-spectral density and time function (magnitude in dB) for Rayleigh fading with Doppler effect]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 4:}$ Shown on the left is the Jakes spectrum | ||
| + | *for $f_{\rm D, \hspace{0.15cm} max} = 50 \ \ \rm Hz$ (blue curve) as well as | ||
| + | *for $f_{\rm D, \hspace{0.15cm} max} = 100 \ \rm Hz$ (red curve). | ||
| + | |||
| + | |||
| + | For [[Examples_of_Communication_Systems/General_Description_of_GSM#Emergence_and_history_of_GSM|$\text{GSM 900}$]] $(f_{\rm S} = 900 \ \rm MHz)$ these values correspond to the speeds $v = 60 \ \rm km/h$ and $v = 120 \ \rm km/h$, respectively. | ||
| − | + | For [[Examples_of_Communication_Systems/General_Description_of_GSM#Emergence_and_history_of_GSM|$\text{GSM 1800}$]] $(f_{\rm S} = 1.8 \ \rm GHz)$ these values apply to half as high speeds: $v = 30 \ \ \rm km/h$ and $v = 60 \ \rm km/h$, resp. | |
| − | + | The right diagram shows the logarithmic absolute value of $z(t)$: | |
| + | *For example you can see the twice as fast fading of the red curve. | ||
| + | *The Rayleigh PDF (amplitude distribution) is independent of $f_{\rm D, \hspace{0.15cm} max}$ and therefore the same for both cases.}}<br> | ||
| − | |||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben:1.4 | + | [[Aufgaben:Exercise 1.4: Rayleigh PDF and Jakes PDS]] |
| − | [[ | + | [[Aufgaben:Exercise 1.4Z: On the Doppler Effect]] |
| − | [[Aufgaben:1.5 | + | [[Aufgaben:Exercise 1.5: Reconstruction of the Jakes Spectrum]] |
{{Display}} | {{Display}} | ||
Latest revision as of 14:31, 29 January 2023
Contents
Some general remarks on ACF and PSD
The correlation between $r(t)$ and $r(t+ \Delta t)$ ⇒ $\text{auto-correlation function}$ $\rm (ACF)$ is suitable for describing the inner statistical dependencies between the neighboring signal values:
- \[\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\big [ r(t) \cdot r^{\star}(t + {\rm \Delta}t)\big ] \hspace{0.05cm}.\]
Compared to the definition under the link above, the following differences can be seen:
- The ACF variable is here marked with $\Delta t$ instead of $\tau$ because in this book we need $\tau$ still for the 2D impulse response $h(t, \hspace{0.05cm}\tau)$ .
- The equivalent low-pass signal $r(t)$ is complex. By the factor $1/2$ however, the ACF $\varphi_r ({\rm \Delta}t)$ and especially the power $\varphi_r ({\rm \Delta}t = 0)$ refer to the (real) band-pass signal $r_{\rm BP}(t)$.
Applying the Rayleigh fading channel model ⇒ $r(t) = s(t) \cdot z(t)$ results for its ACF:
- \[\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\big [ s(t) \cdot z(t) \cdot s^{\star}(t + {\rm \Delta}t) \cdot z^{\star}(t + {\rm \Delta}t)\big ] = \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)\hspace{0.05cm}.\]
For the ACF of the transmitted signal $s(t)$ and the multiplicative factor $z(t)$ the following definitions apply:
- \[ \varphi_s ({\rm \Delta}t)= {1}/{2} \cdot {\rm E}\big [ s(t) \cdot s^{\star}(t + {\rm \Delta}t)\big ] \hspace{0.05cm},\]
- \[\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]\hspace{0.05cm}.\]
The factor $1/2$ is only to be considered for the ACF calculation of band-pass signals in the equivalent low-pass range, but not for $\varphi_z ({\rm \Delta}t)$. Otherwise $\varphi_r ({\rm \Delta}t) \ne \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)$ would result.
Based on the definition of $\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]$ the ACF is always real even with a complex time function $z(t)$ and also with respect to $ {\rm \Delta}t$ even. Let us further consider that
- $z(t) = x(t) + {\rm j} \cdot y(t) $ ,
- $x(t)$ and $y(t)$ have the same statistical properties, and
- that no statistical dependencies exist between $x(t)$ and $y(t)$ ,
so the ACF of the complex factor $z(t)$ can be written as:
- \[\varphi_z ({\rm \Delta}t) = \varphi_x ({\rm \Delta}t) + \varphi_y ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t) \hspace{0.05cm}.\]
$\text{Conclusion:}$ This results in the following simplification:
- To determine the statistical dependencies of the complex variable $z(t)$ only one of the two Gaussian processes must be considered. In the following, this is $x(t)$.
- We first calculate the auto-correlation function $\rm (ACF)$ $\varphi_x ({\rm \Delta}t) = {\rm E}\big[x(t) \cdot x(t + {\rm \Delta}t)\big]$ of the real part and then its power-spectral density $\rm (PSD)$
- \[{\it \Phi}_x (f_{\rm D}) = \int_{-\infty}^{+\infty} \varphi_x ({\rm \Delta}t) \cdot {\rm e}^{ -- {\rm j \cdot 2 \pi} \cdot f_{\rm D} \cdot {\rm \Delta}t } \hspace{0.15cm}{\rm d}( {\rm \Delta}t) \hspace{0.3cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.3cm} \varphi_x ({\rm \Delta}t) \hspace{0.05cm}. \]
- For the corresponding parameters of the complex random process $z(t)$ we have:
- \[\varphi_z ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t)\hspace{0.05cm},\hspace{0.2cm} {\it \Phi}_z (f_{\rm D}) = 2 \cdot {\it \Phi}_x (f_{\rm D}) \hspace{0.05cm}.\]
- The $\rm PSD$ variable is the $\text{Doppler frequency}$ $f_{\rm D}$, because in mobile radio the so-called "Doppler effect" is the cause of the statistical dependencies.
This effect is explained in the next section.
Phenomenological description of the Doppler effect
The statistical dependencies within the real signals $x(t)$ and $y(t)$ or within the complex quantity $z(t)$ are due to the Doppler effect. This was predicted theoretically in the middle of the 19th century by the Austrian mathematician, physicist and astronomer $\text{Christian Andreas Doppler}$ and named after him.
$\text{Definition:}$ The »Doppler effect« refers to the change in the perceived frequency of waves of any kind that occurs when the source (transmitter) and observer (receiver) move relative to each other.
Qualitatively, the Doppler effect can be described as follows:
- If the observer and source approach each other, the frequency increases from the observer's point of view, regardless of whether the observer is moving or the source or both.
- If the source moves away from the observer or the observer moves away from the source, the observer perceives a lower frequency than that actually transmitted.
$\text{Example 1:}$ We look at the pitch change of the "Martinhorn" of an ambulance. As long as the vehicle approaches, the observer hears a higher tone than when the car is stationary. When the ambulance moves away, a lower tone is perceived.
The same effect can be seen with a car racing note. The frequency changes and the sound are the more obvious the faster the cars are going.
In this learning tutorial you can illustrate the subject matter with the interactive applet "The Doppler Effect" .
$\text{Example 2:}$
Some properties of this effect, which is still known from physics lessons, will now be shown by means of snapshots of an earlier version of the above mentioned animation, where the dynamic program properties are of course lost.
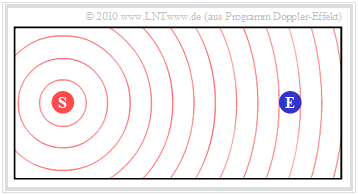
The first diagram shows the initial situation:
- The stationary station $\rm (S)$ outputs the constant frequency $f_{\rm S}$ .
- The wave propagation is illustrated in the diagram by concentric circles around $\rm (S)$ .
- If the receiver $\rm (E)$ is also at rest, the frequency $f_{\rm E} = f_{\rm S}$ is then perceived.
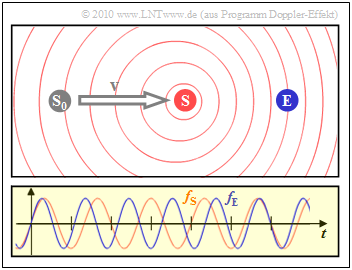
$\text{Example 3:}$ The next snapshot shows the case where the transmitter $\rm (S)$ has moved at constant speed $v$ from its starting point $\rm (S_0)$ towards the receiver $\rm (E)$.
- The right diagram shows that the frequency $f_{\rm E}$ (blue oscillation) perceived by the receiver is larger by about $20\%$ than the frequency $f_{\rm S}$ at the transmitter (red oscillation).
- Due to the movement of the transmitter, the circles are no longer concentric.
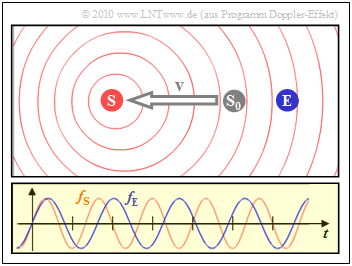
- The scenario shown on the left results when the transmitter $\rm (S)$ moves away from the receiver $\rm (E)$. Then the received frequency $f_{\rm E}$ (blue oscillation) is about $20\%$ smaller than the transmitted frequency $f_{\rm S}$.
$\text{However, the following must be taken into account:}$
- All these figures apply to unrealistically high speed $(v = c/5)$, where $c = 3 \cdot 10^8 \, {\rm m/s}$ indicates the speed of light. In mobile radio, the deviations between $f_{\rm S}$ and $f_{\rm E}$ are usually only a fraction of the transmission frequency.
- The exact equation for the receiving frequency $f_{\rm E}$, including an angle $\alpha$ between the direction of movement and the connecting line transmitter–receiver, is
- \[f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c \cdot \cos(\alpha)} \hspace{0.05cm}.\]
- As the "Exercise 1.4Z" will show: One can assume at realistic speeds $(v \ll c)$ the following approximation, in which the effects described by the $\text{Theory of Relativity}$ are disregarded:
- \[f_{\rm E} \approx f_{\rm S} \cdot \big [1 +{v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.05cm}.\]
Doppler frequency and its distribution
We summarize the statements of the last section briefly, whereby we start from the second, i.e. the non–relativistic equation:
- A relative movement between transmitter (source) and receiver (observer) results in a shift by the Doppler frequency $f_{\rm D} = f_{\rm E} - f_{\rm S}$.
- A positive Doppler frequency $(f_{\rm E} > f_{\rm S})$ results when transmitter and receiver move (relative) towards each other. A negative Doppler frequency $(f_{\rm E} < f_{\rm S})$ means that transmitter and receiver move away from each other (directly or at an angle).
- The maximum frequency shift occurs when transmitter and receiver move directly towards each other ⇒ angle $\alpha = 0^\circ$. This maximum value depends (first approximation) on the transmission frequency $ f_{\rm S}$ and the speed $v$ $(c = 3 \cdot 10^8 \, {\rm m/s}$ indicates the speed of light$)$:
- \[f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.\]
- If the relative movement takes place at any angle $\alpha$ to the connecting line transmitter–receiver, then the Doppler shift is
- \[f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} - \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \le f_{\rm D} \le + \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{0.05cm}.\]
$\text{Conclusion:}$ Assuming equal probable directions of motion $($equal distribution for the angle $\alpha$ in the range $- \pi \le \alpha \le +\pi)$ the probability density function $($here denoted with $\rm wdf$ (from the german WahrscheinlichkeitsDichteFunktion$)$ the Doppler frequency in the range $- f_\text{D, max} \le f_{\rm D} \le + f_\text{D, max}$:
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
Outside the range between $-f_\text{D, max}$ and $+f_\text{D, max}$ the probability density function always has the value zero.
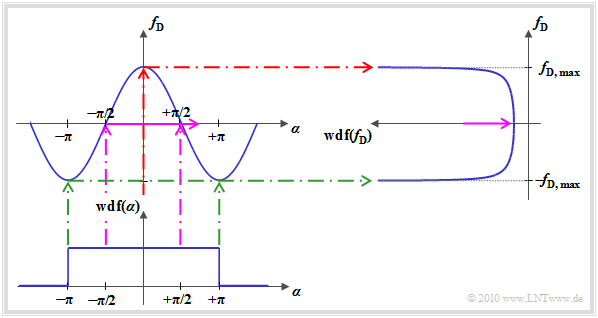
$\text{Derivation:}$ The resulting Doppler frequency depending on the angle of movement $\alpha$ is
- \[f_{\rm D} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) = g(\alpha) \hspace{0.05cm}.\]
We refer to this function as $g(\alpha)$ and assume that
- $\alpha$ takes all angle values between $\pm \pi$
- with equal probability ⇒ equal distribution.
Then for the probability of the Doppler frequency according to the chapter "Transformation of Random Variables" in the book "Stochastic Signal Theory":
- \[{\rm wdf}(f_{\rm D})=\frac{ {\rm wdf}(\alpha)}{\vert g\hspace{0.08cm}'(\alpha)\vert}\Bigg \vert_{\hspace{0.1cm} \alpha=h(f_{\rm D})} \hspace{0.05cm}\]
- with the derivative $g\hspace{0.08cm}'(\alpha)= - f_\text{D, max} \cdot \sin(\alpha)$, and
- the inverse function $ \alpha = h(f_{\rm D})$.
In the example the inverse function is
- $$ \alpha = \arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}).$$
The diagram illustrates the calculation procedure for determining the Doppler frequency's PDF:
- Since the characteristic curve between the Doppler frequency $f_{\rm D}$ and the angle $\alpha$ ⇒ $ g(\alpha) = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha)$ is limited by the value $f_{\rm D, \hspace{0.05cm} max}$ there is for $f_{\rm D}$ no value possible outside this range.
- When transforming random variables, a distinction must be made between areas with positive and negative slopes of the transformation's characteristic curve. The $\alpha$–values between $-\pi$ and $0$ $($positive gradient of the transformation characteristic$)$ provide the result
- \[{\rm wdf}(f_{\rm D})=\frac{1/(2\pi)}{f_{\rm D, \hspace{0.05cm} max} \cdot \sin(\alpha)} \Bigg \vert_{\hspace{0.1cm} \alpha=\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})} = \frac{(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} )^{-1} }{ \sin(\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}))} = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- For reasons of symmetry, the positive $\alpha$–area contributes in the same way, so that the inner total area is given by
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- If $\alpha$ takes values around $\pm \pi/2$ it results in a small Doppler frequency ⇒ $f_{\rm D} \approx 0$ $($violet marking$)$. But, because of the relatively large gradient of the cosine curve $g(\alpha)$ at $\alpha = \pm \pi/2$ the PDF–value at $f_{\rm D} \approx 0$ ist very small.
- Small angles $($around $\alpha \approx 0)$, however, lead to the maximum Doppler frequency ⇒ $f_{\rm D} \approx f_{\rm D, \hspace{0.05cm} max}$ $($red marker$)$. Because of the nearly horizontal characteristic curve $g(\alpha)$ here the $f_{\rm D}$–PDF is clearly larger. For $f_{\rm D} \equiv f_{\rm D, \hspace{0.05cm} max}$ this even results in an infinitely large value.
- On the other hand, if $\alpha$ takes values around $\pm \pi$ it leads to the Doppler frequency $f_{\rm D} \approx -f_{\rm D, \hspace{0.05cm} max}$ $($green marker$)$. Again the characteristic curve is nearly horizontal and this results in a large PDF–value.
ACF and PSD with Rayleigh–Fading
We now assume an antenna with the same radiation in all directions; then the Doppler power-spectral density is identical in shape to the PDF of the Doppler frequencies.
For ${\it \Phi}_x(f_{\rm D})$ the PDF must still be multiplied by the power $\sigma^2$ of the Gaussian process, and the resulting PSD ${\it \Phi}_z(f_{\rm D})$ of the complex factor $z(t) = x(t) + {\rm j} \cdot y(t) $ can be written after doubling as:
- \[{\it \Phi}_z(f_{\rm D}) = \left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} |f_{\rm D}| \le f_{\rm D, \hspace{0.05cm} max} \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.\]
This process is named after $\text{William C. Jakes Jr.}$ the »Jakes spectrum«. The doubling is necessary, because up to now only the contribution of the real part $x(t)$ was considered.
The corresponding auto-correlation function $\rm (ACF)$ is obtained after a $\text{inverse Fourier transformation}$:
- \[\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm},\]
with the Bessel function of first kind and zero order $($first equation: definition, second equation: series expansion$)$:
- \[{\rm J }_0 (u) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{- {\rm j }\hspace{0.03cm}\cdot \hspace{0.03cm}u \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} = \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(-1)^k \cdot (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
The numerical values of this function can be obtained with the "applet of the same name".
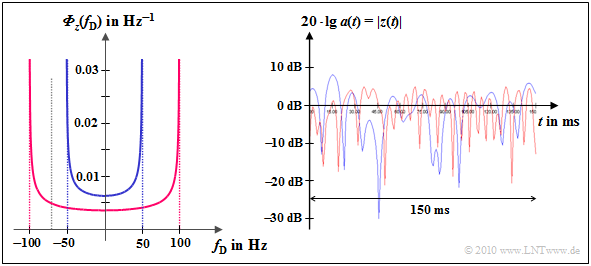
$\text{Example 4:}$ Shown on the left is the Jakes spectrum
- for $f_{\rm D, \hspace{0.15cm} max} = 50 \ \ \rm Hz$ (blue curve) as well as
- for $f_{\rm D, \hspace{0.15cm} max} = 100 \ \rm Hz$ (red curve).
For $\text{GSM 900}$ $(f_{\rm S} = 900 \ \rm MHz)$ these values correspond to the speeds $v = 60 \ \rm km/h$ and $v = 120 \ \rm km/h$, respectively.
For $\text{GSM 1800}$ $(f_{\rm S} = 1.8 \ \rm GHz)$ these values apply to half as high speeds: $v = 30 \ \ \rm km/h$ and $v = 60 \ \rm km/h$, resp.
The right diagram shows the logarithmic absolute value of $z(t)$:
- For example you can see the twice as fast fading of the red curve.
- The Rayleigh PDF (amplitude distribution) is independent of $f_{\rm D, \hspace{0.15cm} max}$ and therefore the same for both cases.
Exercises for the chapter
Exercise 1.4: Rayleigh PDF and Jakes PDS
Exercise 1.4Z: On the Doppler Effect
Exercise 1.5: Reconstruction of the Jakes Spectrum