Difference between revisions of "Information Theory/Natural Discrete Sources"
| (58 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Entropy of Discrete Sources |
| − | |Vorherige Seite= | + | |Vorherige Seite=Discrete Sources with Memory |
| − | |Nächste Seite= | + | |Nächste Seite=General_Description |
}} | }} | ||
| − | == | + | ==Difficulties with the determination of entropy == |
| + | <br> | ||
| + | Up to now, we have been dealing exclusively with artificially generated symbol sequences. Now we consider written texts. Such a text can be seen as a natural discrete message source, which of course can also be analyzed information-theoretically by determining its entropy. | ||
| − | + | Even today (2011), natural texts are still often represented with the 8 bit character set according to ANSI ("American National Standard Institute"), although there are several "more modern" encodings; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The $M = 2^8 = 256$ ANSI characters are used as follows: | ||
| + | * '''No. 0 to 31''': control commands that cannot be printed or displayed, | ||
| − | + | * '''No. 32 to 127''': identical to the characters of the 7 bit ASCII code, | |
| − | |||
| − | |||
| − | |||
| + | * '''No. 128 to 159''': additional control characters or alphanumeric characters for Windows, | ||
| − | + | * '''No. 160 to 255''': identical to the Unicode charts. | |
| − | + | Theoretically, one could also define the entropy here as the border crossing point of the entropy approximation $H_k$ for $k \to \infty$, according to the procedure from the [[Information_Theory/Discrete_Sources_with_Memory#Generalization_to_.7F.27.22.60UNIQ-MathJax111-QINU.60.22.27.7F-tuple_and_boundary_crossing|"last chapter"]]. In practice, however, insurmountable numerical limitations can be found here as well: | |
| − | + | *Already for the entropy approximation $H_2$ there are $M^2 = 256^2 = 65\hspace{0.1cm}536$ possible two-tuples. Thus, the calculation requires the same amount of memory (in bytes). If you assume that you need for a sufficiently safe statistic $100$ equivalents per tuple on average, the length of the source symbol sequence should already be $N > 6.5 · 10^6$. | |
| − | |||
| − | |||
| − | |||
| + | *The number of possible three-tuples is $M^3 > 16 · 10^7$ and thus the required source symbol length is already $N > 1.6 · 10^9$. This corresponds to a book with about $500\hspace{0.1cm}000$ pages to $42$ lines per page and $80$ characters per line. | ||
| − | + | *For a natural text the statistical ties extend much further than two or three characters. Küpfmüller gives a value of $100$ for the German language. To determine the 100th entropy approximation you need $2^{800}$ ≈ $10^{240}$ frequencies and for the safe statistics $100$ times more characters. | |
| − | :1 | + | A justified question is therefore: How did [https://en.wikipedia.org/wiki/Karl_K%C3%BCpfm%C3%BCller $\text{Karl Küpfmüller}$] determine the entropy of the German language in 1954? How did [https://en.wikipedia.org/wiki/Claude_Shannon $\text{Claude Elwood Shannon}$] do the same for the English language, even before Küpfmüller? One thing is revealed beforehand: Not with the approach described above. |
| + | |||
| + | |||
| + | ==Entropy estimation according to Küpfmüller == | ||
| + | <br> | ||
| + | Karl Küpfmüller has investigated the entropy of German texts in his published assessment [Küpf54]<ref name ='Küpf54'>Küpfmüller, K.: Die Entropie der deutschen Sprache. Fernmeldetechnische Zeitung 7, 1954, S. 265-272.</ref>, the following assumptions are made: | ||
| + | *an alphabet with $26$ letters (no umlauts and punctuation marks), | ||
| + | |||
| + | *not taking into account the space character, | ||
| + | |||
| + | *no distinction between upper and lower case. | ||
| + | |||
| + | |||
| + | The maximum average information content is therefore | ||
| + | :$$H_0 = \log_2 (26) ≈ 4.7\ \rm bit/letter.$$ | ||
| + | |||
| + | Küpfmüller's estimation is based on the following considerations: | ||
| + | |||
| + | '''(1)''' The »'''first entropy approximation'''« results from the letter frequencies in German texts. According to a study of 1939, "e" is with a frequency of $16. 7\%$ the most frequent, the rarest is "x" with $0.02\%$. Averaged over all letters we obtain | ||
| + | :$$H_1 \approx 4.1\,\, {\rm bit/letter}\hspace{0.05 cm}.$$ | ||
| + | |||
| + | '''(2)''' Regarding the »'''syllable frequency'''« Küpfmüller evaluates the "Häufigkeitswörterbuch der deutschen Sprache" (Frequency Dictionary of the German Language), published by [https://de.wikipedia.org/wiki/Friedrich_Wilhelm_Kaeding $\text{Friedrich Wilhelm Kaeding}$] in 1898. He distinguishes between root syllables, prefixes, and final syllables and thus arrives at the average information content of all syllables: | ||
| − | :2.) | + | :$$H_{\rm syllable} = \hspace{-0.1cm} H_{\rm root} + H_{\rm prefix} + H_{\rm final} + H_{\rm rest} \approx |
| + | 4.15 + 0.82+1.62 + 2.0 \approx 8.6\,\, {\rm bit/syllable} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | :The following proportions were taken into account: | ||
| + | :*According to the Kaeding study of 1898, the $400$ most common root syllables (beginning with "de") represent $47\%$ of a German text and contribute to the entropy with $H_{\text{root}} ≈ 4.15 \ \rm bit/syllable$. | ||
| + | |||
| + | :*The contribution of $242$ most common prefixes - in the first place "ge" with $9\%$ - is numbered by Küpfmüller with $H_{\text{prefix}} ≈ 0.82 \ \rm bit/syllable$. | ||
| + | |||
| + | :*The contribution of the $118$ most used final syllables is $H_{\text{final}} ≈ 1.62 \ \rm bit/syllable$. Most often, "en" appears at the end of words with $30\%$ . | ||
| + | |||
| + | :*The remaining $14\%$ is distributed over syllables not yet measured. Küpfmüller assumes that there are $4000$ and that they are equally distributed. He assumes $H_{\text{rest}} ≈ 2 \ \rm bit/syllable$ for this. | ||
| + | |||
| + | |||
| + | '''(3)''' As average number of letters per syllable Küpfmüller determined the value $3.03$. From this he deduced the »'''third entropy approximation'''« regarding the letters: | ||
| + | :$$H_3 \approx {8.6}/{3.03}\approx 2.8\,\, {\rm bit/letter}\hspace{0.05 cm}.$$ | ||
| + | |||
| + | '''(4)''' Küpfmüller's estimation of the entropy approximation $H_3$ based mainly on the syllable frequencies according to '''(2)''' and the mean value of $3.03$ letters per syllable. To get another entropy approximation $H_k$ with greater $k$ Küpfmüller additionally analyzed the words in German texts. He came to the following results: | ||
| + | |||
| + | :*The $322$ most common words provide an entropy contribution of $4.5 \ \rm bit/word$. | ||
| − | :$ | + | :*The contributions of the remaining $40\hspace{0.1cm}000$ words were estimated. Assuming that the frequencies of rare words are reciprocal to their ordinal number ([https://en.wikipedia.org/wiki/Zipf%27s_law $\text{Zipf's Law}$]). |
| − | + | ||
| − | + | :*With these assumptions the average information content (related to words) is about $11 \ \rm bit/word$. | |
| + | |||
| + | |||
| + | '''(5)''' The counting "letters per word" resulted in average $5.5$. Analogous to point '''(3)''' the entropy approximation for $k = 5.5$ was approximated. Küpfmüller gives the value: | ||
| + | :$$H_{5.5} \approx {11}/{5.5}\approx 2\,\, {\rm bit/letter}\hspace{0.05 cm}.$$ | ||
| + | :Of course, $k$ can only assume integer values, according to [[Information_Theory/Sources_with_Memory#Generalization to k-tuple and boundary crossing|$\text{its definition}$]]. This equation is therefore to be interpreted in such a way that for $H_5$ a somewhat larger and for $H_6$ a somewhat smaller value than $2 \ {\rm bit/letter}$ will result. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(6)''' Now you can try to get the final value of entropy for $k \to \infty$ by extrapolation from these three points $H_1$, $H_3$ and $H_{5.5}$ : | ||
| + | [[File:EN_Inf_T_1_3_S2.png|right|frame|Approximate values of the entropy of the German language according to Küpfmüller]] | ||
| − | : | + | :*The continuous line, taken from Küpfmüller's original work [Küpf54]<ref name ='Küpf54'>Küpfmüller, K.: Die Entropie der deutschen Sprache. Fernmeldetechnische Zeitung 7, 1954, S. 265-272.</ref>, leads to the final entropy value $H = 1.6 \ \rm bit/letter$. |
| + | :*The green curves are two extrapolation attempts (of a continuous function course through three points) of the $\rm LNTwww$'s author. | ||
| + | :*These and the brown arrows are actually only meant to show that such an extrapolation is (carefully worded) somewhat vague. | ||
| − | |||
| − | + | '''(7)''' Küpfmüller then tried to verify the final value $H = 1.6 \ \rm bit/letter$ found by him with this first estimation with a completely different methodology - see next section. After this estimation he revised his result slightly to | |
| + | :$$H = 1.51 \ \rm bit/letter.$$ | ||
| − | |||
| − | + | '''(8)''' Three years earlier, after a completely different approach, Claude E. Shannon had given the entropy value $H ≈ 1 \ \rm bit/letter$ for the English language, but taking into account the space character. In order to be able to compare his results with Shannom, Küpfmüller subsequently included the space character in his result. | |
| − | |||
| − | |||
| − | |||
| − | : | + | :*The correction factor is the quotient of the average word length without considering the space $(5.5)$ and the average word length with consideration of the space $(5.5+1 = 6.5)$. |
| + | |||
| + | :*This correction led to Küpfmueller's final result: | ||
| + | ::$$H =1.51 \cdot {5.5}/{6.5}\approx 1.3\,\, {\rm bit/letter}\hspace{0.05 cm}.$$ | ||
| − | |||
| − | == | + | ==A further entropy estimation by Küpfmüller == |
| + | <br> | ||
| + | For the sake of completeness, Küpfmüller's considerations are presented here, which led him to the final result $H = 1.51 \ \rm bit/letter$. Since there was no documentation for the statistics of word groups or whole sentences, he estimated the entropy value of the German language as follows: | ||
| + | #Any contiguous German text is covered behind a certain word. The preceding text is read and the reader should try to determine the following word from the context of the preceding text. | ||
| + | #For a large number of such attempts, the percentage of hits gives a measure of the relationships between words and sentences. It can be seen that for one and the same type of text (novels, scientific writings, etc.) by one and the same author, a constant final value of this hit ratio is reached relatively quickly (about one hundred to two hundred attempts). | ||
| + | #The hit ratio, however, depends quite strongly on the type of text. For different texts, values between $15\%$ and $33\%$ are obtained, with the mean value at $22\%$. This also means: On average, $22\%$ of the words in a German text can be determined from the context. | ||
| + | #Alternatively: The word count of a long text can be reduced with the factor $0.78$ without a significant loss of the message content of the text. Starting from the reference value $H_{5. 5} = 2 \ \rm bit/letter$ $($see dot '''(5)''' in the last section$)$ for a word of medium length this results in the entropy $H ≈ 0.78 · 2 = 1.56 \ \rm bit/letter$. | ||
| + | #Küpfmüller verified this value with a comparable empirical study regarding the syllables and thus determined the reduction factor $0.54$ (regarding syllables). Küpfmüller gives $H = 0. 54 · H_3 ≈ 1.51 \ \rm bit/letter$ as the final result, where $H_3 ≈ 2.8 \ \rm bit/letter$ corresponds to the entropy of a syllable of medium length $($about three letters, see point '''(3)''' in the last section$)$ . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The remarks in this and the previous section, which may be perceived as very critical, are not intended to diminish the importance of neither Küpfmüller's entropy estimation, nor Shannon's contributions to the same topic. | ||
| + | *They are only meant to point out the great difficulties that arise in this task. | ||
| − | + | *This is perhaps also the reason why no one has dealt with this problem intensively since the 1950s. | |
| − | == | + | ==Some own simulation results== |
| + | <br> | ||
| + | Karl Küpfmüller's data regarding the entropy of the German language will now be compared with some (very simple) simulation results that were worked out by the author of this chapter (Günter Söder) at the Department of Communications Engineering at the Technical University of Munich as part of an internship for students. The results are based on the German Bible in ASCII format with $N \approx 4.37 \cdot 10^6$ characters. This corresponds to a book with $1300$ pages at $42$ lines per page and $80$ characters per line. | ||
| + | |||
| + | |||
| + | The symbol set size has been reduced to $M = 33$ and includes the characters '''a''', '''b''', '''c''', ... . '''x''', '''y''', '''z''', '''ä''', '''ö''', '''ü''', '''ß''', $\rm BS$, $\rm DI$, $\rm PM$. Our analysis did not differentiate between upper and lower case letters. In contrast to Küpfmüller's analysis, we also took into account: | ||
| + | #The German umlauts '''ä''', '''ö''', '''ü''' and '''ß''', which make up about $1.2\%$ of the biblical text, | ||
| + | #the class "Digits" ⇒ $\rm DI$ with about $1.3\%$ because of the verse numbering within the bible, | ||
| + | #the class "Punctuation Marks" ⇒ $\rm PM$ with about $3\%$, | ||
| + | #the class "Blank Space" ⇒ $\rm BS$ as the most common character $(17.8\%)$, even more than the "e" $(12.8\%)$. | ||
| + | |||
| + | |||
| + | The following table summarizes the results: $N$ indicates the analyzed file size in characters (bytes). The decision content $H_0$ as well as the entropy approximations $H_1$, $H_2$ and $H_3$ were each determined from $N$ characters and are each given in "bit/characters". | ||
| + | |||
| + | [[File:EN_Inf_T_1_3_S3_v2.png|left|frame|Entropy values (in bit/characters) of the German Bible]] | ||
| + | <br> | ||
| + | *Please do not consider these results to be scientific research. | ||
| + | |||
| + | *It is only an attempt to give students an understanding of the subject matter in an internship. | ||
| + | |||
| + | *The basis of this study was the Bible, since we had both its German and English versions available to us in the appropriate ASCII format. | ||
| + | <br clear=all> | ||
| + | The results of the above table can be summarized as follows: | ||
| + | *In all rows the entropy approximations $H_k$ decreases monotously with increasing $k$. The decrease is convex, that means: $H_1 - H_2 > H_2 - H_3$. The extrapolation of the final value $(k \to \infty)$ from the three entropy approximations determined in each case is not possible (or only extremely vague). | ||
| + | |||
| + | *If the evaluation of the digits $\rm (DI)$ and additionally the evaluation of the punctuation marks $\rm (PM)$ is omitted, the approximations $H_1$ $($by $0. 114)$, $H_2$ $($by $0.063)$ and $H_3$ $($by $0.038)$ decrease. On the final entropy $H$ as the limit value of $H_k$ for $k \to \infty$ the omission of digits and punctuation will probably have little effect. | ||
| + | |||
| + | *If one leaves also the blank spaces $(\rm BS)$ out of consideration $($Row 4 ⇒ $M = 30)$, the result is almost the same constellation as Küpfmüller originally considered. The only difference are the rather rare German special characters '''ä''', '''ö''', '''ü''' and '''ß'''. | ||
| + | |||
| + | *The $H_1$–value indicated in the last row $(4.132)$ corresponds very well with the value $H_1 ≈ 4.1$ determined by Küpfmüller. However, with regard to the $H_3$–values there are clear differences: Our analysis results in a larger value $(H_3 ≈ 3.4)$ than Küpfmüller $(H_3 ≈ 2.8)$. | ||
| + | |||
| + | *From the frequency of the blank spaces $(17.8\%)$ here results an average word length of $1/0.178 - 1 ≈ 4.6$, a smaller value than Küpfmüller ($5.5$) had given. The discrepancy can be partly explained with our analysis file "Bible" (many spaces due to verse numbering). | ||
| + | |||
| + | *Interesting is the comparison of lines 3 and 4. If $\rm BS$ is taken into account, then although $H_0$ from $\log_2 \ (30) \approx 4.907$ to $\log_2 \ (31) \approx 4. 954$ enlarges, but thereby reduces $H_1$ $($by the factor $0.98)$, $H_2$ $($by $0.96)$ and $H_3$ $($by $0.93)$. Küpfmüller has intuitively taken this factor into account with $85\%$. | ||
| + | |||
| + | |||
| + | Although we consider this own study to be rather insignificant, we believe that for today's texts the $1.0 \ \rm bit/character$ given by Shannon are somewhat too low for the English language and also Küpfmüllers $1.3 \ \rm bit/character$ for the German language, among other things because: | ||
| + | *The symbol set size today is larger than that considered by Shannon and Küpfmüller in the 1950s; for example, for the ASCII character set $M = 256$. | ||
| − | + | *The multiple formatting options (underlining, bold and italics, indents, colors) further increase the information content of a document. | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Die | + | ==Synthetically generated texts == |
| + | <br> | ||
| + | The graphic shows artificially generated German and English texts, which are taken from [Küpf54]<ref name ='Küpf54'>Küpfmüller, K.: Die Entropie der deutschen Sprache. Fernmeldetechnische Zeitung 7, 1954, S. 265-272.</ref>. The underlying symbol set size is $M = 27$, that means, all letters (without umlauts and '''ß''') and the space character are considered. | ||
| − | [[File: | + | [[File:EN_Inf_T_1_3_S4_v4.png|right|frame|Artificially generated German and English texts]] |
| − | + | *The "Zero-order Character Approximation" assumes equally probable characters in each case. There is therefore no difference between German (red) and English (blue). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *The "First-order Character Approximation" already considers the different frequencies, the higher order approximations also the preceding characters. | |
| − | * | ||
| − | |||
| − | + | *In the "Fourth-order Character Approximation" one can already recognize meaningful words. Here the probability for a new letter depends on the last three characters. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *The "First-order Word Approximation" synthesizes sentences according to the word probabilities. The "Second-order Word Approximation" also considers the previous word. | |
| − | + | ||
| + | |||
| + | Further information on the synthetic generation of German and English texts can be found in the [[Aufgaben:Exercise_1.8:_Synthetically_Generated_Texts|"Exercise 1.8"]]. | ||
| − | == Aufgaben | + | ==Exercises for the chapter== |
| + | <br> | ||
| + | [[Aufgaben:Exercise_1.7:_Entropy_of_Natural_Texts|Exercise 1.7: Entropy of Natural Texts]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.8:_Synthetically_Generated_Texts|Exercise 1.8: Synthetically Generated Texts]] | ||
| + | |||
| − | == | + | ==References== |
| − | </ | + | <references/> |
{{Display}} | {{Display}} | ||
Latest revision as of 16:35, 14 February 2023
Contents
Difficulties with the determination of entropy
Up to now, we have been dealing exclusively with artificially generated symbol sequences. Now we consider written texts. Such a text can be seen as a natural discrete message source, which of course can also be analyzed information-theoretically by determining its entropy.
Even today (2011), natural texts are still often represented with the 8 bit character set according to ANSI ("American National Standard Institute"), although there are several "more modern" encodings;
The $M = 2^8 = 256$ ANSI characters are used as follows:
- No. 0 to 31: control commands that cannot be printed or displayed,
- No. 32 to 127: identical to the characters of the 7 bit ASCII code,
- No. 128 to 159: additional control characters or alphanumeric characters for Windows,
- No. 160 to 255: identical to the Unicode charts.
Theoretically, one could also define the entropy here as the border crossing point of the entropy approximation $H_k$ for $k \to \infty$, according to the procedure from the "last chapter". In practice, however, insurmountable numerical limitations can be found here as well:
- Already for the entropy approximation $H_2$ there are $M^2 = 256^2 = 65\hspace{0.1cm}536$ possible two-tuples. Thus, the calculation requires the same amount of memory (in bytes). If you assume that you need for a sufficiently safe statistic $100$ equivalents per tuple on average, the length of the source symbol sequence should already be $N > 6.5 · 10^6$.
- The number of possible three-tuples is $M^3 > 16 · 10^7$ and thus the required source symbol length is already $N > 1.6 · 10^9$. This corresponds to a book with about $500\hspace{0.1cm}000$ pages to $42$ lines per page and $80$ characters per line.
- For a natural text the statistical ties extend much further than two or three characters. Küpfmüller gives a value of $100$ for the German language. To determine the 100th entropy approximation you need $2^{800}$ ≈ $10^{240}$ frequencies and for the safe statistics $100$ times more characters.
A justified question is therefore: How did $\text{Karl Küpfmüller}$ determine the entropy of the German language in 1954? How did $\text{Claude Elwood Shannon}$ do the same for the English language, even before Küpfmüller? One thing is revealed beforehand: Not with the approach described above.
Entropy estimation according to Küpfmüller
Karl Küpfmüller has investigated the entropy of German texts in his published assessment [Küpf54][1], the following assumptions are made:
- an alphabet with $26$ letters (no umlauts and punctuation marks),
- not taking into account the space character,
- no distinction between upper and lower case.
The maximum average information content is therefore
- $$H_0 = \log_2 (26) ≈ 4.7\ \rm bit/letter.$$
Küpfmüller's estimation is based on the following considerations:
(1) The »first entropy approximation« results from the letter frequencies in German texts. According to a study of 1939, "e" is with a frequency of $16. 7\%$ the most frequent, the rarest is "x" with $0.02\%$. Averaged over all letters we obtain
- $$H_1 \approx 4.1\,\, {\rm bit/letter}\hspace{0.05 cm}.$$
(2) Regarding the »syllable frequency« Küpfmüller evaluates the "Häufigkeitswörterbuch der deutschen Sprache" (Frequency Dictionary of the German Language), published by $\text{Friedrich Wilhelm Kaeding}$ in 1898. He distinguishes between root syllables, prefixes, and final syllables and thus arrives at the average information content of all syllables:
- $$H_{\rm syllable} = \hspace{-0.1cm} H_{\rm root} + H_{\rm prefix} + H_{\rm final} + H_{\rm rest} \approx 4.15 + 0.82+1.62 + 2.0 \approx 8.6\,\, {\rm bit/syllable} \hspace{0.05cm}.$$
- The following proportions were taken into account:
- According to the Kaeding study of 1898, the $400$ most common root syllables (beginning with "de") represent $47\%$ of a German text and contribute to the entropy with $H_{\text{root}} ≈ 4.15 \ \rm bit/syllable$.
- The contribution of $242$ most common prefixes - in the first place "ge" with $9\%$ - is numbered by Küpfmüller with $H_{\text{prefix}} ≈ 0.82 \ \rm bit/syllable$.
- The contribution of the $118$ most used final syllables is $H_{\text{final}} ≈ 1.62 \ \rm bit/syllable$. Most often, "en" appears at the end of words with $30\%$ .
- The remaining $14\%$ is distributed over syllables not yet measured. Küpfmüller assumes that there are $4000$ and that they are equally distributed. He assumes $H_{\text{rest}} ≈ 2 \ \rm bit/syllable$ for this.
(3) As average number of letters per syllable Küpfmüller determined the value $3.03$. From this he deduced the »third entropy approximation« regarding the letters:
- $$H_3 \approx {8.6}/{3.03}\approx 2.8\,\, {\rm bit/letter}\hspace{0.05 cm}.$$
(4) Küpfmüller's estimation of the entropy approximation $H_3$ based mainly on the syllable frequencies according to (2) and the mean value of $3.03$ letters per syllable. To get another entropy approximation $H_k$ with greater $k$ Küpfmüller additionally analyzed the words in German texts. He came to the following results:
- The $322$ most common words provide an entropy contribution of $4.5 \ \rm bit/word$.
- The contributions of the remaining $40\hspace{0.1cm}000$ words were estimated. Assuming that the frequencies of rare words are reciprocal to their ordinal number ($\text{Zipf's Law}$).
- With these assumptions the average information content (related to words) is about $11 \ \rm bit/word$.
(5) The counting "letters per word" resulted in average $5.5$. Analogous to point (3) the entropy approximation for $k = 5.5$ was approximated. Küpfmüller gives the value:
- $$H_{5.5} \approx {11}/{5.5}\approx 2\,\, {\rm bit/letter}\hspace{0.05 cm}.$$
- Of course, $k$ can only assume integer values, according to $\text{its definition}$. This equation is therefore to be interpreted in such a way that for $H_5$ a somewhat larger and for $H_6$ a somewhat smaller value than $2 \ {\rm bit/letter}$ will result.
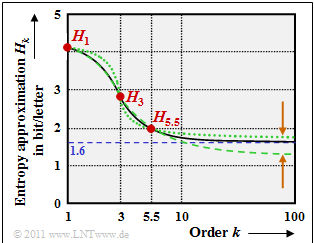
(6) Now you can try to get the final value of entropy for $k \to \infty$ by extrapolation from these three points $H_1$, $H_3$ and $H_{5.5}$ :
- The continuous line, taken from Küpfmüller's original work [Küpf54][1], leads to the final entropy value $H = 1.6 \ \rm bit/letter$.
- The green curves are two extrapolation attempts (of a continuous function course through three points) of the $\rm LNTwww$'s author.
- These and the brown arrows are actually only meant to show that such an extrapolation is (carefully worded) somewhat vague.
(7) Küpfmüller then tried to verify the final value $H = 1.6 \ \rm bit/letter$ found by him with this first estimation with a completely different methodology - see next section. After this estimation he revised his result slightly to
- $$H = 1.51 \ \rm bit/letter.$$
(8) Three years earlier, after a completely different approach, Claude E. Shannon had given the entropy value $H ≈ 1 \ \rm bit/letter$ for the English language, but taking into account the space character. In order to be able to compare his results with Shannom, Küpfmüller subsequently included the space character in his result.
- The correction factor is the quotient of the average word length without considering the space $(5.5)$ and the average word length with consideration of the space $(5.5+1 = 6.5)$.
- This correction led to Küpfmueller's final result:
- $$H =1.51 \cdot {5.5}/{6.5}\approx 1.3\,\, {\rm bit/letter}\hspace{0.05 cm}.$$
A further entropy estimation by Küpfmüller
For the sake of completeness, Küpfmüller's considerations are presented here, which led him to the final result $H = 1.51 \ \rm bit/letter$. Since there was no documentation for the statistics of word groups or whole sentences, he estimated the entropy value of the German language as follows:
- Any contiguous German text is covered behind a certain word. The preceding text is read and the reader should try to determine the following word from the context of the preceding text.
- For a large number of such attempts, the percentage of hits gives a measure of the relationships between words and sentences. It can be seen that for one and the same type of text (novels, scientific writings, etc.) by one and the same author, a constant final value of this hit ratio is reached relatively quickly (about one hundred to two hundred attempts).
- The hit ratio, however, depends quite strongly on the type of text. For different texts, values between $15\%$ and $33\%$ are obtained, with the mean value at $22\%$. This also means: On average, $22\%$ of the words in a German text can be determined from the context.
- Alternatively: The word count of a long text can be reduced with the factor $0.78$ without a significant loss of the message content of the text. Starting from the reference value $H_{5. 5} = 2 \ \rm bit/letter$ $($see dot (5) in the last section$)$ for a word of medium length this results in the entropy $H ≈ 0.78 · 2 = 1.56 \ \rm bit/letter$.
- Küpfmüller verified this value with a comparable empirical study regarding the syllables and thus determined the reduction factor $0.54$ (regarding syllables). Küpfmüller gives $H = 0. 54 · H_3 ≈ 1.51 \ \rm bit/letter$ as the final result, where $H_3 ≈ 2.8 \ \rm bit/letter$ corresponds to the entropy of a syllable of medium length $($about three letters, see point (3) in the last section$)$ .
The remarks in this and the previous section, which may be perceived as very critical, are not intended to diminish the importance of neither Küpfmüller's entropy estimation, nor Shannon's contributions to the same topic.
- They are only meant to point out the great difficulties that arise in this task.
- This is perhaps also the reason why no one has dealt with this problem intensively since the 1950s.
Some own simulation results
Karl Küpfmüller's data regarding the entropy of the German language will now be compared with some (very simple) simulation results that were worked out by the author of this chapter (Günter Söder) at the Department of Communications Engineering at the Technical University of Munich as part of an internship for students. The results are based on the German Bible in ASCII format with $N \approx 4.37 \cdot 10^6$ characters. This corresponds to a book with $1300$ pages at $42$ lines per page and $80$ characters per line.
The symbol set size has been reduced to $M = 33$ and includes the characters a, b, c, ... . x, y, z, ä, ö, ü, ß, $\rm BS$, $\rm DI$, $\rm PM$. Our analysis did not differentiate between upper and lower case letters. In contrast to Küpfmüller's analysis, we also took into account:
- The German umlauts ä, ö, ü and ß, which make up about $1.2\%$ of the biblical text,
- the class "Digits" ⇒ $\rm DI$ with about $1.3\%$ because of the verse numbering within the bible,
- the class "Punctuation Marks" ⇒ $\rm PM$ with about $3\%$,
- the class "Blank Space" ⇒ $\rm BS$ as the most common character $(17.8\%)$, even more than the "e" $(12.8\%)$.
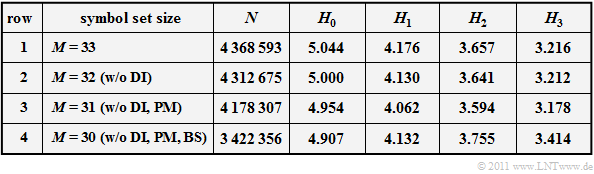
The following table summarizes the results: $N$ indicates the analyzed file size in characters (bytes). The decision content $H_0$ as well as the entropy approximations $H_1$, $H_2$ and $H_3$ were each determined from $N$ characters and are each given in "bit/characters".
- Please do not consider these results to be scientific research.
- It is only an attempt to give students an understanding of the subject matter in an internship.
- The basis of this study was the Bible, since we had both its German and English versions available to us in the appropriate ASCII format.
The results of the above table can be summarized as follows:
- In all rows the entropy approximations $H_k$ decreases monotously with increasing $k$. The decrease is convex, that means: $H_1 - H_2 > H_2 - H_3$. The extrapolation of the final value $(k \to \infty)$ from the three entropy approximations determined in each case is not possible (or only extremely vague).
- If the evaluation of the digits $\rm (DI)$ and additionally the evaluation of the punctuation marks $\rm (PM)$ is omitted, the approximations $H_1$ $($by $0. 114)$, $H_2$ $($by $0.063)$ and $H_3$ $($by $0.038)$ decrease. On the final entropy $H$ as the limit value of $H_k$ for $k \to \infty$ the omission of digits and punctuation will probably have little effect.
- If one leaves also the blank spaces $(\rm BS)$ out of consideration $($Row 4 ⇒ $M = 30)$, the result is almost the same constellation as Küpfmüller originally considered. The only difference are the rather rare German special characters ä, ö, ü and ß.
- The $H_1$–value indicated in the last row $(4.132)$ corresponds very well with the value $H_1 ≈ 4.1$ determined by Küpfmüller. However, with regard to the $H_3$–values there are clear differences: Our analysis results in a larger value $(H_3 ≈ 3.4)$ than Küpfmüller $(H_3 ≈ 2.8)$.
- From the frequency of the blank spaces $(17.8\%)$ here results an average word length of $1/0.178 - 1 ≈ 4.6$, a smaller value than Küpfmüller ($5.5$) had given. The discrepancy can be partly explained with our analysis file "Bible" (many spaces due to verse numbering).
- Interesting is the comparison of lines 3 and 4. If $\rm BS$ is taken into account, then although $H_0$ from $\log_2 \ (30) \approx 4.907$ to $\log_2 \ (31) \approx 4. 954$ enlarges, but thereby reduces $H_1$ $($by the factor $0.98)$, $H_2$ $($by $0.96)$ and $H_3$ $($by $0.93)$. Küpfmüller has intuitively taken this factor into account with $85\%$.
Although we consider this own study to be rather insignificant, we believe that for today's texts the $1.0 \ \rm bit/character$ given by Shannon are somewhat too low for the English language and also Küpfmüllers $1.3 \ \rm bit/character$ for the German language, among other things because:
- The symbol set size today is larger than that considered by Shannon and Küpfmüller in the 1950s; for example, for the ASCII character set $M = 256$.
- The multiple formatting options (underlining, bold and italics, indents, colors) further increase the information content of a document.
Synthetically generated texts
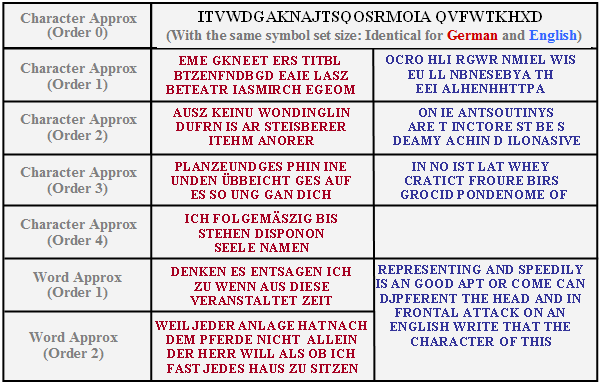
The graphic shows artificially generated German and English texts, which are taken from [Küpf54][1]. The underlying symbol set size is $M = 27$, that means, all letters (without umlauts and ß) and the space character are considered.
- The "Zero-order Character Approximation" assumes equally probable characters in each case. There is therefore no difference between German (red) and English (blue).
- The "First-order Character Approximation" already considers the different frequencies, the higher order approximations also the preceding characters.
- In the "Fourth-order Character Approximation" one can already recognize meaningful words. Here the probability for a new letter depends on the last three characters.
- The "First-order Word Approximation" synthesizes sentences according to the word probabilities. The "Second-order Word Approximation" also considers the previous word.
Further information on the synthetic generation of German and English texts can be found in the "Exercise 1.8".
Exercises for the chapter
Exercise 1.7: Entropy of Natural Texts
Exercise 1.8: Synthetically Generated Texts
References