Difference between revisions of "Aufgaben:Exercise 4.6: OVSF Codes"
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS |
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_A_4_6a.png|right|frame|Tree structure for the construction <br>of an OVSF code]] |
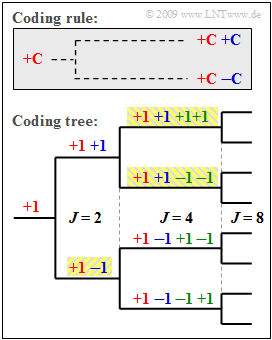
| − | + | The spreading codes for UMTS should | |
| − | * | + | *all be orthogonal to each other to avoid mutual interference between subscribers, |
| − | * | + | *be as flexible as possible in order to realize different spreading factors $J$ . |
| − | + | An example of this are the so-called '''Orthogonal Variable Spreading Factor''' ('''OVSF''') codes, which provide spreading codes of lengths from $J = 4$ to $J = 512$ . These can be created using a code tree, as shown in the diagram. Thereby, at each branch from one code $\mathcal{C}$ two new codes are created. | |
| − | *$(+C +C)$, | + | *$(+\mathcal{C} \ +\hspace{-0.05cm}\mathcal{C})$, |
| − | *$(+C | + | *$(+\mathcal{C}\ -\hspace{-0.05cm}\mathcal{C})$. |
| − | + | The diagram illustrates the principle given here by the example $J = 4$. | |
| + | |||
| + | If we number the spreading sequences from $0$ to $J -1$ we get here the spreading sequences | ||
:$$ \langle c_\nu^{(0)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ | :$$ \langle c_\nu^{(0)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ | ||
:$$\langle c_\nu^{(2)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$ | :$$\langle c_\nu^{(2)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$ | ||
| − | + | According to this nomenclature, for the spreading factor $J = 8$ there are the spreading sequences $\langle c_{\nu}^{(0)} \rangle, \ \text{...} \ ,\langle c_{\nu}^{(7)} \rangle$. | |
| + | |||
| + | Note that no predecessor and successor of a code may be used by other participants. | ||
| + | *So, in the example, four spreading codes with spreading factor $J = 4$ could be used, or. | ||
| + | *the three codes highlighted in yellow - once with $J = 2$ and twice with $J = 4$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS|"Telecommunications Aspects of UMTS"]]. | ||
| + | *Reference is made in particular to the page [[Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS#Spreading_codes_and_scrambling_with_UMTS|"Spreading codes and scrambling with UMTS"]]. | ||
| + | |||
| − | |||
| − | |||
| − | + | ===Questions=== | |
| − | |||
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Construct the tree diagram for $J = 8$. What are the resulting OVSF codes? |
|type="[]"} | |type="[]"} | ||
| − | + $\langle c_{\nu}^{(1)} \rangle | + | + $\langle c_{\nu}^{(1)} \rangle = +1 +1 +1 -1 -1 -1$, |
| − | - $\langle c_{\nu}^{(3)} \rangle | + | - $\langle c_{\nu}^{(3)} \rangle = +1 +1 -1 +1 -1 -1$, |
| − | + $\langle c_{\nu}^{(5)} \rangle | + | + $\langle c_{\nu}^{(5)} \rangle = +1 -1 +1 -1 +1 +1$, |
| − | + $\langle c_{\nu}^{(7)} \rangle | + | + $\langle c_{\nu}^{(7)} \rangle = +1 -1 -1 +1 +1 -1$. |
| − | { | + | {How many UMTS subscribers can be served with $J = 8$ maximum? |
|type="{}"} | |type="{}"} | ||
$K_{\rm max} \ = \ ${ 8 3% } | $K_{\rm max} \ = \ ${ 8 3% } | ||
| − | { | + | {How many subscribers can be served if three of them are to use a spreading code with $J = 4$ ? |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 5 3% } | $K \ = \ $ { 5 3% } | ||
| − | { | + | {Assume a tree structure for $J = 32$ . Is the following assignment feasible: <br>Twice $J = 4$, once $J = 8$, twice $J = 16$, eight times $J = 32$ ? |
| − | |type=" | + | |type="()"} |
| − | + | + | + Yes. |
| − | - | + | - No. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
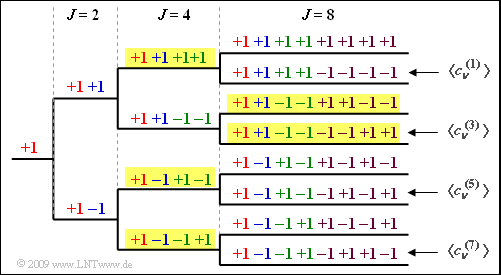
| − | '''(1)''' | + | [[File:P_ID1979__Bei_A_4_6a.png|right|frame|OVSF tree structure for $J = 8$]] |
| − | + | '''(1)''' The graph shows the OVSF tree structure for $J = 8$ user. | |
| + | *From this it can be seen that <u>proposed solutions 1, 3, and 4</u> are true, but not the second one. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' If each user is assigned a spreading code with $J = 8$ then $\underline{K_{\rm max} = 8}$ subscribers can be served. | ||
| + | |||
| + | '''(3)''' If three subscribers are served with $J = 4$ only two subscribers can be served by a spreading sequence with $J = 8$ (see exemplary yellow background in above diagram) ⇒ $\underline{K = 5}$. | ||
| − | |||
| − | |||
| − | '''(4)''' | + | '''(4)''' We denote by. |
| − | *$K_{4} = 2$ | + | *$K_{4} = 2$ the number of spreading sequences with $J = 4$, |
| − | *$K_{8} = 1$ | + | *$K_{8} = 1$ the number of spreading sequences with $J = 8$, |
| − | *$K_{16} = 2$ | + | *$K_{16} = 2$ the number of spreading sequences with $J = 16$, |
| − | *$K_{32} = 8$ | + | *$K_{32} = 8$ the number of spreading sequences with $J = 32$. |
| − | + | Then the following condition must be satisfied: | |
| − | :$$ K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 | + | :$$ K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 \hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} K_4 \cdot8 + K_8 \cdot 4 +K_{16} \cdot2 +K_{32} \cdot1 \le 32 \hspace{0.05cm}.$$ | |
| − | + | *Because $2 \cdot 8 + 1 \cdot 4 + 2 \cdot 2 + 8 = 32$ the desired allocation is just allowed ⇒ <u>Answer YES</u>. | |
| + | *Providing the degree of spread twice $J = 4$ blocks, for example, the top half of the tree, after providing one spread with $J = 8$, three of the eight branches remain to be occupied at the $J = 8$ level, and so on. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 82: | Line 101: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^4.3 Telecommunications Aspects |
^]] | ^]] | ||
Latest revision as of 19:45, 2 March 2023
The spreading codes for UMTS should
- all be orthogonal to each other to avoid mutual interference between subscribers,
- be as flexible as possible in order to realize different spreading factors $J$ .
An example of this are the so-called Orthogonal Variable Spreading Factor (OVSF) codes, which provide spreading codes of lengths from $J = 4$ to $J = 512$ . These can be created using a code tree, as shown in the diagram. Thereby, at each branch from one code $\mathcal{C}$ two new codes are created.
- $(+\mathcal{C} \ +\hspace{-0.05cm}\mathcal{C})$,
- $(+\mathcal{C}\ -\hspace{-0.05cm}\mathcal{C})$.
The diagram illustrates the principle given here by the example $J = 4$.
If we number the spreading sequences from $0$ to $J -1$ we get here the spreading sequences
- $$ \langle c_\nu^{(0)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$
- $$\langle c_\nu^{(2)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$
According to this nomenclature, for the spreading factor $J = 8$ there are the spreading sequences $\langle c_{\nu}^{(0)} \rangle, \ \text{...} \ ,\langle c_{\nu}^{(7)} \rangle$.
Note that no predecessor and successor of a code may be used by other participants.
- So, in the example, four spreading codes with spreading factor $J = 4$ could be used, or.
- the three codes highlighted in yellow - once with $J = 2$ and twice with $J = 4$.
Hints:
- This exercise belongs to the chapter "Telecommunications Aspects of UMTS".
- Reference is made in particular to the page "Spreading codes and scrambling with UMTS".
Questions
Solution
(1) The graph shows the OVSF tree structure for $J = 8$ user.
- From this it can be seen that proposed solutions 1, 3, and 4 are true, but not the second one.
(2) If each user is assigned a spreading code with $J = 8$ then $\underline{K_{\rm max} = 8}$ subscribers can be served.
(3) If three subscribers are served with $J = 4$ only two subscribers can be served by a spreading sequence with $J = 8$ (see exemplary yellow background in above diagram) ⇒ $\underline{K = 5}$.
(4) We denote by.
- $K_{4} = 2$ the number of spreading sequences with $J = 4$,
- $K_{8} = 1$ the number of spreading sequences with $J = 8$,
- $K_{16} = 2$ the number of spreading sequences with $J = 16$,
- $K_{32} = 8$ the number of spreading sequences with $J = 32$.
Then the following condition must be satisfied:
- $$ K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_4 \cdot8 + K_8 \cdot 4 +K_{16} \cdot2 +K_{32} \cdot1 \le 32 \hspace{0.05cm}.$$
- Because $2 \cdot 8 + 1 \cdot 4 + 2 \cdot 2 + 8 = 32$ the desired allocation is just allowed ⇒ Answer YES.
- Providing the degree of spread twice $J = 4$ blocks, for example, the top half of the tree, after providing one spread with $J = 8$, three of the eight branches remain to be occupied at the $J = 8$ level, and so on.