Difference between revisions of "Aufgaben:Exercise 4.5: Pseudo Noise Modulation"
From LNTwww
| (26 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS}} |
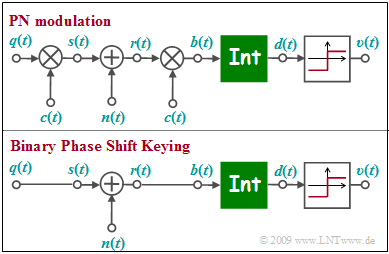
| − | [[File: | + | [[File:EN_Bei_A_4_5.png|right|frame|Models of PN modulation (top) and BPSK (bottom)]] |
| − | + | The upper diagram shows the equivalent circuit of $\rm PN$ modulation $($Direct-Sequence Spread Spectrum, abbreviated $\rm DS–SS)$ in the equivalent low-pass range, based on AWGN noise $n(t)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Shown below is the low-pass model of binary phase shift keying $\rm (BPSK)$. | ||
| + | *The low-pass transmitted signal $s(t)$ is set equal to the rectangular source signal $q(t) ∈ \{+1, –1\}$ with rectangular duration $T$ for reasons of uniformity. | ||
| − | + | *The function of the integrator can be described as follows: | |
| + | :$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | ||
| − | + | *The two models differ by multiplication with the $±1$ spreading signal $c(t)$ at transmitter and receiver, where only the spreading factor $J$ is known from $c(t)$. | |
| − | |||
| − | === | + | |
| + | It has to be investigated whether the lower BPSK model can also be used for PN modulation and whether the BPSK error probability | ||
| + | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ | ||
| + | is also valid for PN modulation, or how the given equation should be modified. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *This exercise mostly refers to the page [[Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS|"Telecommunications Aspects of UMTS"]]. | ||
| + | |||
| + | *For the solution of this exercise, the specification of the specific spreading sequence $($M-sequence or Walsh function$)$ is not important. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | + | {Which detection signal values are possible with BPSK (in the noise-free case)? | |
| − | { | ||
|type="[]"} | |type="[]"} | ||
| − | - $d( | + | - $d(νT)$ can be Gaussian distributed. |
| − | - $d( | + | - $d(νT)$ can take the values $+1$, $0$ and $-1$. |
| − | + | + | + Only the values $d(νT) = +1$ and $d(νT) = -1$ are possible. |
| − | { | + | {Which values are possible in PN modulation (in the noise-free) case? |
|type="[]"} | |type="[]"} | ||
| − | - $d( | + | - $d(νT)$ can be Gaussian distributed. |
| − | - $d( | + | - $d(νT)$ can take the values $+1$, $0$ and $-1$. |
| − | + | + | + Only the values $d(νT) = +1$ and $d(νT) = -1$ are possible. |
| − | { | + | {What modification must be made to the BPSK model to make it applicable to PN modulation? |
|type="[]"} | |type="[]"} | ||
| − | + | + The noise $n(t)$ must be replaced by $n'(t) = n(t) · c(t)$. | |
| − | + | - The integration must now be done over $J · T$. | |
| − | - | + | - The noise power $σ_n^2$ must be reduced by a factor of $J$. |
| − | { | + | {What is the bit error probability $(p_{\rm B})$ for $10 \lg \ (E_{\rm B}/N_0) = 6\ \rm dB$ for PN modulation? <u>Note:</u> For BPSK applies in this case: $p_{\rm B} ≈ 2.3 · 10^{–3}$. |
| − | |type=" | + | |type="()"} |
| − | - | + | - The larger $J$ is chosen, the smaller $p_{\rm B}$ is. |
| − | - | + | - The larger $J$ is chosen, the larger $p_{\rm B}$ is. |
| − | + | + | + Independent of $J$, the value $p_{\rm B} ≈ 2.3 · 10^{–3}$ is always obtained. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| + | '''(1)''' The <u>last solution</u> is correct: | ||
| + | *We are dealing here with an optimal receiver. | ||
| − | + | *Without noise, the signal $b(t)$ within each bit is constantly equal to $+1$ or $-1$. | |
| − | |||
| − | |||
| − | + | *From the given equation for the integrator | |
| + | :$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t $$ | ||
| + | :it follows that $d(νT)$ can take only the values $+1$ and $-1$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | { | + | '''(2)''' Again the <u>last solution</u> is correct: |
| + | * In the noise-free and interference-free case ⇒ $n(t) = 0$, the twofold multiplication by $c(t) ∈ \{+1, –1\}$ can be omitted, | ||
| + | |||
| + | *so that the upper model is identical to the lower model. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' <u>Solution 1</u> is correct: | ||
| + | *Since both models are identical in the noise-free case, only the noise signal has to be adjusted: $n'(t) = n(t) · c(t)$. | ||
| + | |||
| + | *In contrast, the other two solutions are not applicable: | ||
| + | |||
| + | *The integration must still be done over $T = J · T_c$ and the PN modulation does not reduce the AWGN noise. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' The <u>last solution</u> is correct: | ||
| + | *Multiplying the AWGN noise by the high-frequency $±1$ signal $c(t)$, the product is also Gaussian and white. | ||
| + | *Because of ${\rm E}\big[c^2(t)\big] = 1$, the noise variance is not changed either. Thus: | ||
| + | |||
| + | *The equation $p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt {{2 E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$ valid for BPSK is also applicable for PN modulation, independent of spreading factor $J$ and specific spreading sequence. | ||
| + | *Ergo: For AWGN noise, band spreading neither increases nor decreases the error probability. | ||
| + | {{ML-Fuß}} | ||
| − | |||
| − | ^]] | + | [[Category:Examples of Communication Systems: Exercises|^4.3 Telecommunications Aspects^]] |
Latest revision as of 18:22, 4 March 2023
The upper diagram shows the equivalent circuit of $\rm PN$ modulation $($Direct-Sequence Spread Spectrum, abbreviated $\rm DS–SS)$ in the equivalent low-pass range, based on AWGN noise $n(t)$.
Shown below is the low-pass model of binary phase shift keying $\rm (BPSK)$.
- The low-pass transmitted signal $s(t)$ is set equal to the rectangular source signal $q(t) ∈ \{+1, –1\}$ with rectangular duration $T$ for reasons of uniformity.
- The function of the integrator can be described as follows:
- $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$
- The two models differ by multiplication with the $±1$ spreading signal $c(t)$ at transmitter and receiver, where only the spreading factor $J$ is known from $c(t)$.
It has to be investigated whether the lower BPSK model can also be used for PN modulation and whether the BPSK error probability
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
is also valid for PN modulation, or how the given equation should be modified.
Notes:
- This exercise mostly refers to the page "Telecommunications Aspects of UMTS".
- For the solution of this exercise, the specification of the specific spreading sequence $($M-sequence or Walsh function$)$ is not important.
Questions
Solution
(1) The last solution is correct:
- We are dealing here with an optimal receiver.
- Without noise, the signal $b(t)$ within each bit is constantly equal to $+1$ or $-1$.
- From the given equation for the integrator
- $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t $$
- it follows that $d(νT)$ can take only the values $+1$ and $-1$.
(2) Again the last solution is correct:
- In the noise-free and interference-free case ⇒ $n(t) = 0$, the twofold multiplication by $c(t) ∈ \{+1, –1\}$ can be omitted,
- so that the upper model is identical to the lower model.
(3) Solution 1 is correct:
- Since both models are identical in the noise-free case, only the noise signal has to be adjusted: $n'(t) = n(t) · c(t)$.
- In contrast, the other two solutions are not applicable:
- The integration must still be done over $T = J · T_c$ and the PN modulation does not reduce the AWGN noise.
(4) The last solution is correct:
- Multiplying the AWGN noise by the high-frequency $±1$ signal $c(t)$, the product is also Gaussian and white.
- Because of ${\rm E}\big[c^2(t)\big] = 1$, the noise variance is not changed either. Thus:
- The equation $p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt {{2 E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$ valid for BPSK is also applicable for PN modulation, independent of spreading factor $J$ and specific spreading sequence.
- Ergo: For AWGN noise, band spreading neither increases nor decreases the error probability.