Difference between revisions of "Aufgaben:Exercise 4.5Z: About Spread Spectrum with UMTS"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS |
}} | }} | ||
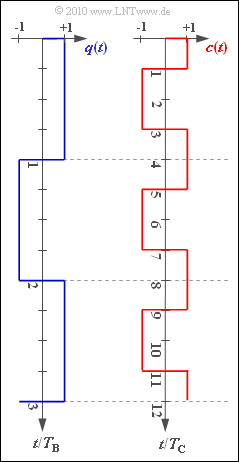
| − | [[File:P_ID1974__Bei_Z_4_5.png|right|frame| | + | [[File:P_ID1974__Bei_Z_4_5.png|right|frame|Source signal and spread signal]] |
| − | + | With UMTS/CDMA, the so-called "Pseudo-noise modulation" is applied. Or: "Direct Sequence Spread Spectrum": | |
| − | * | + | *The rectangular digital signal $q(t)$ is thereby multiplied by the spreading signal $c(t)$ to give the transmitted signal $s(t)$. |
| − | * | + | |
| − | * | + | *This is higher in frequency than $q(t)$ by the spreading factor $J$, and is referred to as "spread spectrum". |
| + | |||
| + | *At the receiver, the same spreading signal $c(t)$ is multiplied in phase synchronism, reversing the spreading process ⇒ "despreading". | ||
| + | |||
| + | |||
| + | The graph shows example signal waveforms for $q(t)$ and $c(t)$. | ||
| + | In the subtask '''(5)''' is asked about transmit chips. For example, the "transmit chip" $s_{3}$ denotes the constant signal value of $s(t)$ in the time interval $2 T_{\rm C} ... 3 T_{\rm C}$. | ||
| − | |||
| Line 19: | Line 24: | ||
| − | |||
| − | * | + | Hints: |
| − | * | + | |
| − | * | + | *This exercise mostly refers to the page [[Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS|"Telecommunications Aspects of UMTS"]]. |
| + | *For calculation of chip duration $T_{\rm C}$ reference is made to the theory page [[Examples_of_Communication_Systems/UMTS_Network_Architecture#Physical_channels|"Physical channels"]] in the chapter "UMTS network architecture". | ||
| + | *There you will find, among other things, the information that on the so-called ''Dedicated Physical Channel''' ('''DPCH''' ) in ten milliseconds exactly $15 \cdot 2560$ chips are transmitted. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - With UMTS, the bit duration $T_{\rm B}$ is fixed. |
| − | + | + | + For UMTS, the chip duration $T_{\rm C}$ is fixed. |
| − | - | + | - Both quantities depend on the channel conditions. |
| − | { | + | {Specify the chip duration $T_{\rm C}$ and chip rate $R_{\rm C}$ in the downlink. |
|type="{}"} | |type="{}"} | ||
$T_{\rm C} \hspace{0.28cm} = \ $ { 0.26 3% } $ \ \rm µ s$ | $T_{\rm C} \hspace{0.28cm} = \ $ { 0.26 3% } $ \ \rm µ s$ | ||
$R_{\rm C} \hspace{0.2cm} = \ $ { 3.84 3% } $ \ \rm Mchip/s$ | $R_{\rm C} \hspace{0.2cm} = \ $ { 3.84 3% } $ \ \rm Mchip/s$ | ||
| − | { | + | {What spreading factor can be read from the graph on the information page? |
|type="{}"} | |type="{}"} | ||
$J \ = \ ${ 4 } | $J \ = \ ${ 4 } | ||
| − | { | + | {What is the bit rate at this spreading factor? |
|type="{}"} | |type="{}"} | ||
$ R_{\rm B} \ = \ $ { 960 3% } $ \ \rm kbit/s$ | $ R_{\rm B} \ = \ $ { 960 3% } $ \ \rm kbit/s$ | ||
| − | { | + | {What are the values $(\pm 1)$ of the "chips" of the transmitted signal $s(t)$? |
|type="{}"} | |type="{}"} | ||
$s_{3} \ = \ $ { -1.03--0.97 } | $s_{3} \ = \ $ { -1.03--0.97 } | ||
| Line 60: | Line 66: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>answer 2</u>: |
| − | * | + | *Fixed for UMTS is the chip duration $T_{\rm C}$, which is still to be calculated in the subtask '''(2)'''. |
| − | + | *The larger the spreading degree $J$ is, the larger the bit duration is. | |
| − | |||
| − | |||
| − | |||
| + | '''(2)''' According to the note on the information page, exactly $15 \cdot 2560 = 38400$ chips are transferred in ten milliseconds. | ||
| + | *Thus the chip rate $R_{\rm C} = 100 \cdot 38400 \ {\rm chips/s} \hspace{0.15cm}\underline{= 3.84 \ \rm Mchip/s}$. | ||
| + | *The chip duration is the reciprocal of this: $T_{\rm C} \hspace{0.15cm}\underline{\approx 0.26 \ \rm µ s}$. | ||
| − | |||
| − | '''( | + | '''(3)''' Each data bit consists of four spreading chips ⇒ $\underline{J = 4}$. |
| − | '''(5)''' | + | |
| + | '''(4)''' The bit rate is given by $J = 4$ to $R_{\rm B} \hspace{0.15cm}\underline{= 960 \ \rm kbit/s}$. | ||
| + | *With the maximum spreading factor for UMTS $J = 512 $, on the other hand, the bit rate is only more $7.5 \ \rm kbit/s$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' For the transmitted signal $s(t) = q(t) \cdot c(t)$. | ||
| + | *The chips $s_{3}$ and $s_{4}$ of the transmitted signal belong to the first data bit $(q_{1} = +1)$: | ||
:$$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$ | :$$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$ | ||
| − | + | *In contrast, the two other transmitting chips we are looking for are associated with the second data bit $(q_{2} = -1)$ : | |
:$$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$ | :$$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$ | ||
| Line 88: | Line 100: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^4.3 Telecommunications Aspects^]] |
| − | |||
| − | |||
| − | ^]] | ||
Latest revision as of 14:33, 5 March 2023
With UMTS/CDMA, the so-called "Pseudo-noise modulation" is applied. Or: "Direct Sequence Spread Spectrum":
- The rectangular digital signal $q(t)$ is thereby multiplied by the spreading signal $c(t)$ to give the transmitted signal $s(t)$.
- This is higher in frequency than $q(t)$ by the spreading factor $J$, and is referred to as "spread spectrum".
- At the receiver, the same spreading signal $c(t)$ is multiplied in phase synchronism, reversing the spreading process ⇒ "despreading".
The graph shows example signal waveforms for $q(t)$ and $c(t)$.
In the subtask (5) is asked about transmit chips. For example, the "transmit chip" $s_{3}$ denotes the constant signal value of $s(t)$ in the time interval $2 T_{\rm C} ... 3 T_{\rm C}$.
Hints:
- This exercise mostly refers to the page "Telecommunications Aspects of UMTS".
- For calculation of chip duration $T_{\rm C}$ reference is made to the theory page "Physical channels" in the chapter "UMTS network architecture".
- There you will find, among other things, the information that on the so-called Dedicated Physical Channel ('DPCH ) in ten milliseconds exactly $15 \cdot 2560$ chips are transmitted.
Questions
Solution
(1) Correct is the answer 2:
- Fixed for UMTS is the chip duration $T_{\rm C}$, which is still to be calculated in the subtask (2).
- The larger the spreading degree $J$ is, the larger the bit duration is.
(2) According to the note on the information page, exactly $15 \cdot 2560 = 38400$ chips are transferred in ten milliseconds.
- Thus the chip rate $R_{\rm C} = 100 \cdot 38400 \ {\rm chips/s} \hspace{0.15cm}\underline{= 3.84 \ \rm Mchip/s}$.
- The chip duration is the reciprocal of this: $T_{\rm C} \hspace{0.15cm}\underline{\approx 0.26 \ \rm µ s}$.
(3) Each data bit consists of four spreading chips ⇒ $\underline{J = 4}$.
(4) The bit rate is given by $J = 4$ to $R_{\rm B} \hspace{0.15cm}\underline{= 960 \ \rm kbit/s}$.
- With the maximum spreading factor for UMTS $J = 512 $, on the other hand, the bit rate is only more $7.5 \ \rm kbit/s$.
(5) For the transmitted signal $s(t) = q(t) \cdot c(t)$.
- The chips $s_{3}$ and $s_{4}$ of the transmitted signal belong to the first data bit $(q_{1} = +1)$:
- $$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$
- In contrast, the two other transmitting chips we are looking for are associated with the second data bit $(q_{2} = -1)$ :
- $$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$