Difference between revisions of "Exercise 2.5Z: Range and Bit Rate with ADSL"
m (Guenter moved page Exercise 2.5Z: Reach and Bit Rate with ADSL to Exercise 2.5Z: Range and Bit Rate with ADSL) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 4: | Line 4: | ||
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_Z_2_5.png|right|frame|"Range vs. bit rate" diagram]] |
The development of xDSL technology began in 1995 with the first standard for $\rm ADSL$ (''Asymmetric Digital Subscriber Line''). From 2006, the faster $\rm VDSL$ (''Very High Data Rate Digital Subscriber Line'') also came into use in Germany. | The development of xDSL technology began in 1995 with the first standard for $\rm ADSL$ (''Asymmetric Digital Subscriber Line''). From 2006, the faster $\rm VDSL$ (''Very High Data Rate Digital Subscriber Line'') also came into use in Germany. | ||
Latest revision as of 18:34, 25 March 2023
The development of xDSL technology began in 1995 with the first standard for $\rm ADSL$ (Asymmetric Digital Subscriber Line). From 2006, the faster $\rm VDSL$ (Very High Data Rate Digital Subscriber Line) also came into use in Germany.
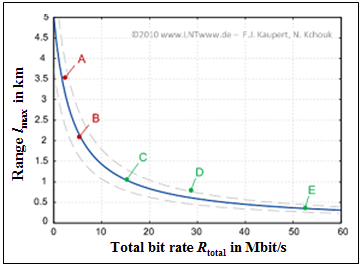
The graph shows five system variants in a diagram in which the achievable cable length $l_{\rm max}$ is plotted as a function of the total bit rate $R_{\rm ges}$ :
- $\boldsymbol{\rm A}\text{:} \hspace{0.3cm} \text{ Bitraten} \ 0.2 \ {\rm Mbit/s} + 2 \ {\rm Mbit/s}; \hspace{0.2cm} \text{ cable length } l_{\rm max} \approx 3.5 \ {\rm km},$
- $\boldsymbol{\rm B}\text{:} \hspace{0.3cm} \text{ Bitraten} \ 0.2 \ {\rm Mbit/s} + 6 \ {\rm Mbit/s}; \hspace{0.2cm} \text{ cable length } l_{\rm max} \approx 2 \ {\rm km},$
- $\boldsymbol{\rm C}\text{:} \hspace{0.3cm} \text{ Bitraten} \ 2 \ {\rm Mbit/s} + 13 \ {\rm Mbit/s}; \hspace{0.3cm} \text{ cable length } l_{\rm max} \approx 1 \ {\rm km},$
- $\boldsymbol{\rm D}\text{:} \hspace{0.3cm} \text{ Bitraten} \ 2 \ {\rm Mbit/s} + 26 \ {\rm Mbit/s}; \hspace{0.3cm} \text{ cable length } \ l_{\rm max} \approx 0.8 \ {\rm km},$
- $\boldsymbol{\rm E}\text{:} \hspace{0.3cm}\text{ Bitraten} \ 2 \ {\rm Mbit/s} + 51 \ {\rm Mbit/s}; \hspace{0.35cm} \text{ cable length } l_{\rm max} \approx 0.4 \ {\rm km}.$
To this graphic is to be noted further:
- All data applies to a balanced copper pair with $\text{0.4 mm}$ diameter.
- One of the bit rates given here is for upstream, the other is for downstream.
- The total bitrate is the sum of the two portions.
- Which bit rate refers to the upstream and which to the downstream is asked in the subtask (1).
- The colored differentiation of the drawn points refers to the subdivision into ADSL and VDSL. This is referred to in the subtask (2).
- The curve drawn in blue shows a rule of thumb that approximates the relationship between range and total bit rate:
- $$l_{\rm max}\,{\rm \big [in}\,\,{\rm km \big]} = \frac {20}{4 + R_{\rm ges}\,{\rm \big[in}\,\,{\rm Mbit/s\big]}} \hspace{0.05cm}.$$
- Dashed are deviations from this by $\pm 25\%$.
One often characterizes a wireline transmission system by the cable attenuation at half the bit rate (note the "a" in the attenuation):
- $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R_{\rm B}}/{2}) = \alpha_{\rm K}(f = {R_{\rm B}}/{2}) \cdot l\hspace{0.05cm}.$$
The attenuation coefficient (noted as "alpha") is given for a $\text{0.4 mm}$ balanced copper pair as follows:
- $$\alpha_{\rm K}(f ) = \left [ 5.1 + 14.3 \cdot \left ({f}/({\rm 1\,MHz})\right )^{0.59} \right ] {\rm dB}/{\rm km} \hspace{0.05cm}.$$
For the downlink of variant $\boldsymbol{\rm A}$ with $R_{\rm B} = 2 \ \rm Mbit/s$ thus results with $l = l_{\rm max} = 3.5 \ \rm km$:
- $$\alpha_{\rm K}(f = {\rm 1\,MHz}) = \left [ 5.1 + 14.3 \right ] {\rm dB}/{\rm km} = 19.4\,{\rm dB}/{\rm km}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm a}_{\rm \star} = 19.4\,{\rm dB}/{\rm km} \cdot 3.5\,{\rm km} = 67.9\,{\rm dB}\hspace{0.05cm}.$$
The values for the other system variants are to be determined in subtask (4).
Hint:
- This exercise belongs to the chapter "Methods to Reduce the Bit Error Rate in DSL".
Questions
Solution
- In all xDSL variants, the downstream is operated at a higher bit rate than the upstream.
- This principle results from user behavior. One fetches much more data to the computer (downstream) than in the reverse direction.
(2) Correct is the second proposed solution:
- VDSL offers higher data rates.
- High data rate, however, is only possible with relatively short line lengths.
(3) The range of such a Gbit/s system over two-wire line would be about $20/1000 \ {\rm km} \underline{= 20 \ \rm meters}$.
- Consider this subtask rather academic.
(4) Here the following characteristic cable attenuations result. For
- variant $\boldsymbol{\rm B} \ (R_{\rm B}/2 = 3 {\rm \ Mbit/s}, \ l_{\rm max} = 2 {\rm \ km})\text{:}$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 3^{0.59} \right ] \cdot 2\,{\rm dB}\hspace{0.15cm}\underline{ \approx 64.9\,{\rm dB}}\hspace{0.05cm},$$
- variant $\boldsymbol{\rm C} \ (R_{\rm B}/2 = 6.5 {\rm \ Mbit/s}, \ l_{\rm max} = 1 {\rm \ km})\text{:}$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 6.5^{0.59} \right ] \cdot 1\,{\rm dB} \hspace{0.15cm}\underline{\approx 48.2\,{\rm dB}}\hspace{0.05cm},$$
- variant $\boldsymbol{\rm D} \ (R_{\rm B}/2 = 13 {\rm \ Mbit/s}, \ l_{\rm max} = 0.8 {\rm \ km})\text{:}$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 13^{0.59} \right ] \cdot 0.8\,{\rm dB}\hspace{0.15cm}\underline{ \approx 56\,{\rm dB}}\hspace{0.05cm},$$
- variant $\boldsymbol{\rm E} \ (R_{\rm B}/2 = 25.5 {\rm \ Mbit/s}, \ l_{\rm max} = 0.4 {\rm \ km})\text{:}$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 25.5^{0.59} \right ] \cdot 0.4\,{\rm dB}\hspace{0.15cm}\underline{ \approx 40.7\,{\rm dB}}\hspace{0.05cm}.$$
Further, it should be noted:
- The characteristic cable attenuation ${\rm a}_{\ast}$ of ADSL systems is in the range $65 \ \rm dB$ ... $68 \ \rm dB$.
- The VDSL variants provide characteristic cable attenuations between $40 \ \rm dB$ and $56 \ \rm dB$.
- It should be noted, however, that this system parameter ${\rm a}_{\ast}$, which is important in conventional binary baseband transmission, does not reflect the conditions in OFDM or Discrete Multitone Transmission sufficiently well.